1.2. Пифагоровы тройки

Изучение свойств натуральных чисел привело пифагорейцев к еще одной «вечной» проблеме теоретической арифметики (теории чисел) — проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древнем Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение

Сегодня эта задача именуется задачей Пифагора, а ее решения — тройки натуральных чисел, удовлетворяющих уравнению (1.2.1), — называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами x, y и целочисленной гипотенузой z.

Рис. 36.

Частные решения задачи Пифагора были известны в глубокой древности. В папирусе времен фараона Аменемхета I (ок. 2000 до н. э.), хранящемся в Египетском музее в Берлине, мы находим прямоугольный треугольник с отношением сторон ( ). По мнению крупнейшего немецкого историка математики М. Кантора (1829 — 1920), в Древнем Египте существовала особая профессия гарпедонаптов — «натягивателей веревок», которые во время торжественной церемонии закладки храмов и пирамид размечали прямые углы с помощью веревки, имеющей 12 (= 3 + 4 + 5) равноотстоящих узлов. Способ построения прямого угла гарпедонаптами очевиден из рисунка 36.

Надо сказать, что с Кантором категорически не согласен другой знаток древней математики — ван дер Варден, хотя сами пропорции древнеегипетской архитектуры свидетельствуют в пользу Кантора. Как бы то ни было, сегодня прямоугольный треугольник с отношением сторон называется египетским.

Как отмечалось на с. 76, сохранилась глиняная табличка, относящаяся к древневавилонской эпохе и содержащая 15 строк пифагоровых троек. Помимо тривиальной тройки, получаемой из египетской (3, 4, 5) умножением на 15 (45, 60, 75), здесь есть и весьма сложные пифагоровы тройки, такие, как (3367, 3456, 4825) и даже (12709, 13500, 18541)! Нет никаких сомнений, что эти числа были найдены не простым перебором, а по неким единым правилам.

И тем не менее вопрос об общем решении уравнения (1.2.1) в натуральных числах был поставлен и решен только пифагорейцами. Общая постановка какой бы то ни было математической задачи была чужда как древним египтянам, так и древним вавилонянам. Только с Пифагора начинается становление математики как дедуктивной науки, и одним из первых шагов на этом пути было решение задачи о пифагоровых тройках. Первые решения уравнения (1.2.1) античная традиция связывает с именами Пифагора и Платона. Попробуем реконструировать эти решения.

Рис. 37.

Ясно, что уравнение (1.2.1) Пифагор мыслил не в аналитической форме, а в виде квадратного числа , внутри которого нужно было отыскать квадратные числа и . Число естественно было представить в виде квадрата со стороной y на единицу меньше стороны z исходного квадрата, т. е. . Тогда, как легко видеть из рисунка 37 (именно видеть!), для оставшегося квадратного числа должно выполняться равенство . Таким образом, мы приходим к системе линейных уравнений

Складывая и вычитая эти уравнения, находим решение уравнения (1.2.1):

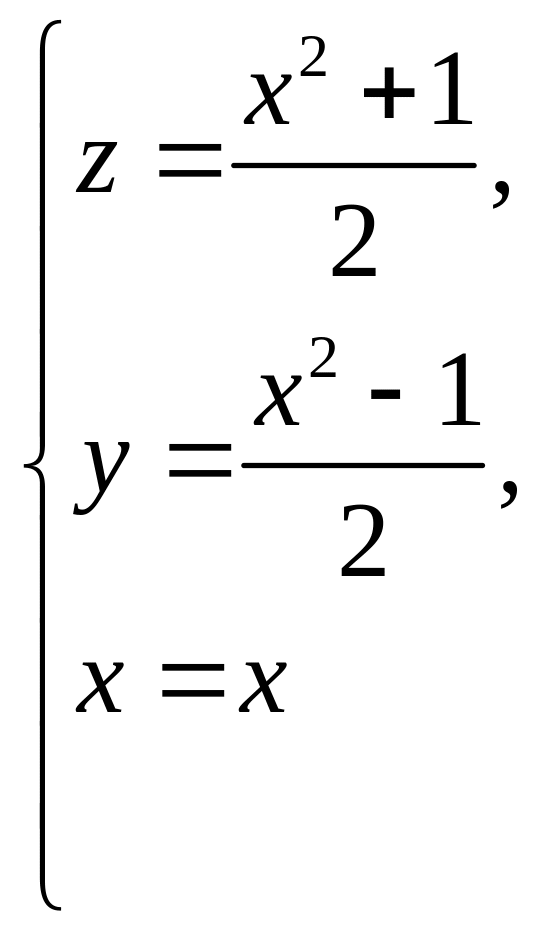
Легко убедиться в том, что полученное решение дает натуральные числа только при нечетных . Таким образом, окончательно имеем

и т. д. Это решение традиция связывает с именем Пифагора.

Заметим, что система (1.2.2) может быть получена и формально из уравнения (1.2.1). В самом деле,

откуда, полагая , приходим к (1.2.2).

Ясно, что решение Пифагора найдено при достаточно жестком ограничении ( ) и содержит далеко не все пифагоровы тройки. Следующим шагом можно положить , тогда , так как только в этом случае будет квадратным числом. Так возникает система

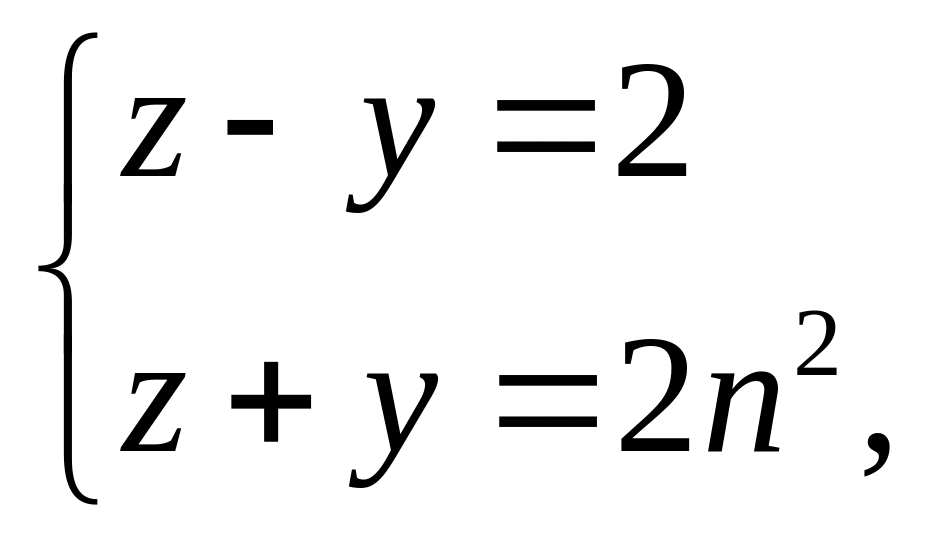
решение которой имеет вид

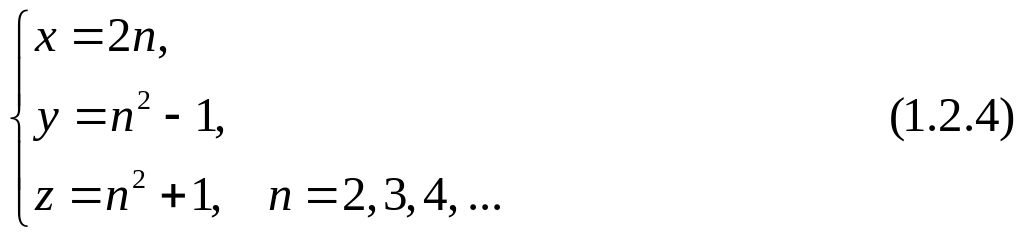
и т. д. Автором этого решения часто называют Платона.

Легко видеть, что тройки Платона (1.2.4) при нечетных n и после сокращения на 2 дают тройки Пифагора (1.2.3), т. е. решение Платона является более общим. И хотя решение Платона не исчерпывает всего множества решений уравнения (1.2.1), путь получения общего решения теперь просматривается. Найдем это решение.

Прежде всего заметим, что искать следует только примитивные пифагоровы тройки , для которых (символ НОД, как обычно, обозначает наибольший общий делитель), ибо ясно, что если — пифагорова тройка, то для любого натурального также будет пифагоровой тройкой. Теперь может быть доказана основная

Теорема. Если p и q взаимно простые числа разной четности , то все примитивные пифагоровы тройки находятся по формулам

Доказательство

1. Для пифагоровых троек условие влечет

В самом деле, если, например, , то делится на в силу того, что , т. е. z делится на k, или , что противоречит условию.

2. Для любой примитивной пифагоровой тройки числа x, y разной четности. Действительно, x и y не могут быть оба четными в силу (*). Если x и y оба нечетные, т. е. , то , т. е. делится на 2, но не на 4. Итак, четно, тогда z тоже четно (см. с. 121), т. е. , значит, делится на 4. Получили противоречие.

3. Положим для определенности . Тогда т. е. нечетно и, следовательно, z нечетно, т. е. . Тогда и , следовательно, .

4. Покажем, что α и β взаимно простые числа разной четности.

а) Пусть , т. е. . Тогда

что противоречит (*).

б) Пусть . Тогда

что противоречит (*).

в) Аналогично доказывается, что α и β одновременно не могут быть нечетными.

5. Итак, , тогда , причем и взаимно простые числа разной четности. Но тогда p и q также являются взаимно простыми числами разной четности, причем

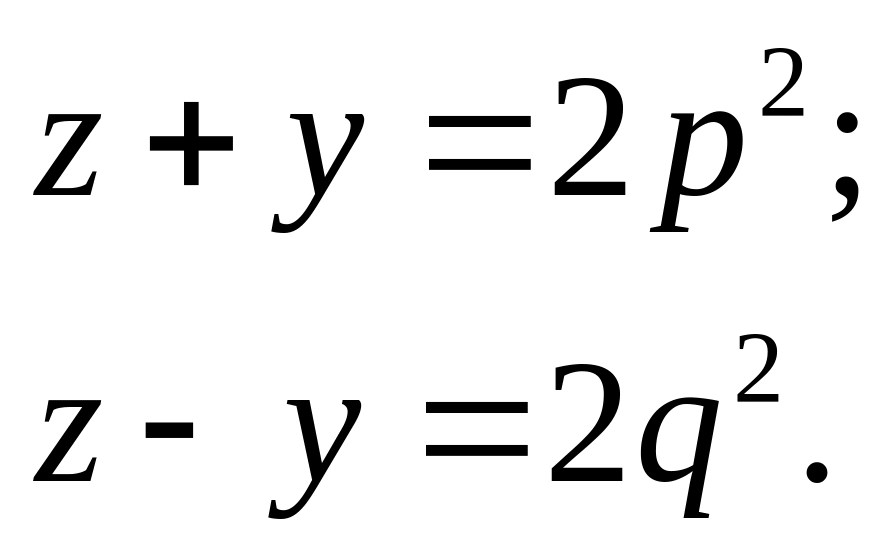
Отсюда легко находим: .

Теорема доказана. Ясно, что при (1.2.5) переходит в (1.2.4). Решение (1.2.5) при любых натуральных дает всевозможные пифагоровы тройки без учета их примитивности. Оно было хорошо известно в античную эпоху и указано в таких великих книгах древности, как «Начала» Евклида (III в. до н. э.) и «Арифметика» Диофанта (III в. н. э.). На этом можно было бы поставить точку, но...

Около 1630 г. скромный юрист из французского города Тулузы Пьер Ферма (1601 — 1665), проводивший свободное от работы время в математических упражнениях, на полях «Арифметики» Диофанта против того места, где Диофант решает задачу Пифагора, сделал запись: «Наоборот, невозможно разложить куб на два куба или биквадрат на два биквадрата и вообще никакую степень выше второй нельзя разложить на сумму двух степеней с теми же показателями. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки».

Так, на полях Диофантовой «Арифметики» Ферма сформулировал утверждение, вошедшее в историю математики как великая теорема Ферма: для любого натурального уравнение

не имеет решений в целых положительных числах x, y, z.

Однако общее доказательство теоремы, обещанное Ферма, бесследно исчезло: вместо него в бумагах Ферма было найдено лишь частное доказательство для случая . Не нашли это доказательство и поныне лучшие математические умы мира.

Прошло более 350 лет, в течение которых предпринимались героические усилия для доказательства коварной теоремы. В 1770 г. Л. Эйлер доказал теорему для , в 1825 г. П. Дирихле и А. Лежандр — для в 1839 г. Г. Ламе — для . Затем Э. Куммер наметил общий подход к проблеме и доказал теорему для всех простых чисел n из промежутка [3; 100]. Страсти вокруг теоремы Ферма накалялись. В 1907 г. за ее доказательство была объявлена международная премия в 100 000 немецких марок. Теорема Ферма стала каким-то математическим наваждением.

К настоящему времени с помощью ЭВМ установлено, что . Последняя сенсация облетела математический мир в 1993 г.: английский математик Эндрю Уайлс из Пристонского университета в докладе, сделанном в Институте математических наук имени Исаака Ньютона Кембриджского университета перед 75 виднейшими математиками мира, представил доказательство теоремы Ферма. Время покажет: будет ли в нем обнаружена ошибка, как и в великом множестве предыдущих доказательств, или нет.

Тем не менее, все эти поиски и прежде всего идеи российского математика А. Паршина нельзя назвать бесполезными. Они породили массу новых плодотворных направлений в математике и, таким образом, необычайно обогатили саму математику.

Так, начатое Пифагором во времена, когда человечество знало лишь натуральные числа, исследование «безобидного» уравнения

привело к сложнейшей проблеме современной теории чисел — исследованию в целых числах уравнения

— великой и неприступной на протяжении четырех столетий теореме Ферма.