3. Дифференциальные уравнения второго порядка. Однородные дифференциальные уравнения второго порядка.

Дифференциальное уравнение вида называется дифференциальным уравнением второго порядка..

Общее решение уравнения зависит от двух неопределенных постоянных и и записывается в форме . Задача Коши для дифференциального уравнения второго порядка решается при начальных условиях:

.

Если дифференциальное уравнение второго порядка не содержит какой-либо из величин или , то оно называется неполным.

Алгоритм решения.

Преобразовать в дифференциальное уравнение первого порядка путем введения новой переменной .

Пример. - неполное дифференциальное уравнение второго порядка.

Найти частное решение уравнения , удовлетворяющее начальным условиям: -задача Коши для дифференциального уравнения второго порядка.

Уравнение вида , (1)

называют однородным уравнением.

Однородное уравнение обладает тем свойством, что, если и являются его частными решениями, то выражение (2) также будет решением данного уравнения при произвольных значениях постоянных и .

Уравнение вида (3) называется однородным уравнением с постоянными коэффициентами

Алгоритм решения.

1. Составляем характеристическое уравнение .

2. Решая квадратное уравнение, будем иметь

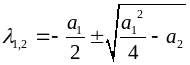. (4)

Возможны варианты решения:

1. .

В этом случае выражение (4) определяет два различных значения и . Общее решение уравнения запишем в виде:

. (5)

2. .

Теперь квадратное уравнение имеет только один корень .

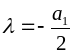Общее решение однородного уравнения запишется в форме

. (6)

3. .

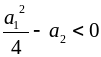Квадратное уравнение имеет комплексные корни и .

Общее решение однородного уравнения будет

. (7)

Примеры. , , однородные уравнения с постоянными коэффициентами.

Замечание. Задача Коши для однородных дифференциальных уравнений с постоянными коэффициентами всегда имеет единственное решение.

4. Линейные дифференциальные уравнения второго порядка.

Уравнение вида . (1)

называется линейным дифференциальным уравнением второго порядка.

Уравнение вида (2) называется линейным дифференциальным уравнением с постоянными коэффициентами

Алгоритм решения.

1. Определяем общее решение соответствующего однородного уравнения .

2. Подбираем частное решение линейного уравнения (2) (см. таблицу). Если правая часть уравнения состоит из суммы двух функций специального вида, то частное решение искать в виде . Если правая часть не принадлежит к функциям «специального вида», то подобрать вид частного решения по виду правой части и корням характеристического уравнения нельзя. В данном случае применяется метод вариации произвольных постоянных.

3. Общее решение (2) получается путем сложения по формуле .

Таблица.

Правая часть дифференциального уравнения	Корни характеристического уравнения	Вид частного решения
f(x) = Pm (x), где Pm (x) – многочлен степени m.	а) Число 0 не является корнем характеристического уравнения.	Qm (x), где Qm (x) – многочлен степени не выше m.
	б) Число 0 является корнем характеристического уравнения кратности k.	xkQm(x)
f(x) = eαx Pm (x), где α-вещественное число.	а) Число α не является корнем характеристического уравнения.	Qm (x)eαx
	б) Число α является корнем характеристического уравнения кратности k.	xk Qm (x)eαx
f(x)=Pm(x)cosβx+Qm(x)sinβx, где Pm(x) и Qm(x) – многочлены степени не выше m и хоть один из них имеет степень m.	а) Число βi не является корнем характеристического уравнения.	um(x)cosβx+vm(x)sinβx, где um(x) и vm(x) – многочлены степени не выше m.
	б) Число βi является корнем характеристического уравнения кратности k.	xk (um(x)cosβx+vm(x)sinβx)
f(x)= eαx (Pm(x)cosβx+Qm(x)sinβx)	а) Число α+βi не является корнем характеристического уравнения.	eαx (um(x)cosβx+vm(x)sinβx)
	б) Число α+βi является корнем характеристического уравнения кратности k.	xk eαx (um(x)cosβx+vm(x)sinβx)

Примеры: - линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.