
Облакова Т.В. ТВ (2 семестр)-занятие1 ФН-11 (2016)
Занятие 1. Комбинаторика. Основные комбинаторные правила
1. Правило суммы
Если
множество
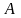 содержит
содержит
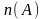 элементов, а множество
элементов, а множество
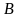 –
–
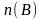 элементов и пересечение множеств
и
пусто,
элементов и пересечение множеств
и
пусто,
 ,
то число элементов в их объединении
,
то число элементов в их объединении
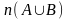 равно сумме элементов множеств
и
:
равно сумме элементов множеств
и
:
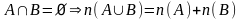 .
.
Число элементов во множестве называется его мощностью.
Пример 1. Сколько существует способов поставить белопольного слона на шахматную доску, чтобы он держал под боем больше 10 полей.
Р ешение.
Всего на шахматной доске 32 белых клетки.
Количество полей, находящихся под боем
зависит от расстояния до края доски.
Так, если слон стоит на одном из крайних
полей (их 14 штук), то он держит под боем
7 полей. Если же он занимает клетку,
отстоящую от края на один ряд (10 позиций),
то – 9 полей. Если подвинуть слона еще
ближе к центру (6 возможных позиций), то
число полей под боем возрастет до 11,
наконец, для двух центральных полей это
число составит 13. Таким образом, для
ответа на вопрос задачи достаточно
сложить число возможностей для третьего
и четвертого случаев: 6+2=8.
ешение.
Всего на шахматной доске 32 белых клетки.
Количество полей, находящихся под боем
зависит от расстояния до края доски.
Так, если слон стоит на одном из крайних
полей (их 14 штук), то он держит под боем
7 полей. Если же он занимает клетку,
отстоящую от края на один ряд (10 позиций),
то – 9 полей. Если подвинуть слона еще
ближе к центру (6 возможных позиций), то
число полей под боем возрастет до 11,
наконец, для двух центральных полей это
число составит 13. Таким образом, для
ответа на вопрос задачи достаточно
сложить число возможностей для третьего
и четвертого случаев: 6+2=8.
Т еорема.
Если множество
содержит
элементов, а множество
–
элементов и пересечение множеств
и
не пусто,
еорема.
Если множество
содержит
элементов, а множество
–
элементов и пересечение множеств
и
не пусто,
 ,
то число элементов в их объединении
вычисляется по формуле:
,
то число элементов в их объединении
вычисляется по формуле:
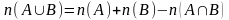 .
.
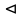 Доказательство.
Множество
Доказательство.
Множество
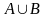 и множество
можно представить как объединение двух
непересекающихся множеств:
и множество
можно представить как объединение двух
непересекающихся множеств:
 ,
,
 .
Тогда по правилу суммы имеем:
.
Тогда по правилу суммы имеем:
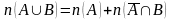 (1)
(1)
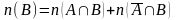 .
(2)
.
(2)
Вычитая
из выражения (1) выражение (2), получаем:

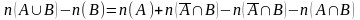
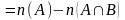 .
.
Окончательно
имеем:
,
что и требовалось доказать.
Методом математической индукции формулу можно обобщить на сумму любого конечного числа множеств. В частности для трех конечных множеств имеем.
Следствие.
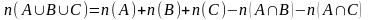
 (3)
(3)
Пример 2. В школе работают кружки: математический, английского языка и спортивный. В математическом кружке занимается 150 учеников, в кружке английского языка - 80 учеников, в спортивном - 110 учеников. В кружках английского языка и спортивном занимаются 60 учеников, в математическом и спортивном - 70 учеников, в кружках математическом и английском - 40 учеников. Во всех трех кружках занимается 21 ученик. Ни один кружок не посещает 14 учеников. Найти число учащихся в школе.
Введем следующие обозначения:
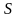 -
множество учеников школы - основное
множество;
-
множество учеников школы - основное
множество;
- множество учеников, посещающих кружок английского языка;
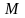 -
множество учеников, состоящих в
математическом кружке;
-
множество учеников, состоящих в
математическом кружке;
 -
множество учеников, занимающихся в
спортивном кружке
-
множество учеников, занимающихся в
спортивном кружке
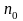 -
число учеников, не занимающихся ни в
одном кружке.
-
число учеников, не занимающихся ни в
одном кружке.
По
условию
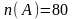 ,
,
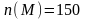 ,
,
 ,
,
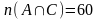 ,
,
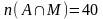 ,
,
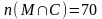 ,
,
 ,
,
 .
.
Тогда
число учеников в школе
 можно вычислить по формуле (3).
можно вычислить по формуле (3).
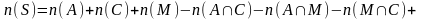
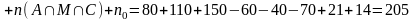 .
.
2. Правило произведения
Пусть
заданы два конечных множества
 и
и
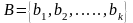 .
Тогда множество всех возможных
упорядоченных пар в их декартовом
произведении
.
Тогда множество всех возможных
упорядоченных пар в их декартовом
произведении
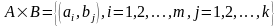 равно произведению чисел элементов в
каждом из этих множеств:
равно произведению чисел элементов в
каждом из этих множеств:
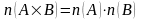 .
.
Пример 3. В урне лежат пять белых шаров, перенумерованных цифрами 1, 2, 3, 4, 5, три красных шара перенумерованных цифрами 1, 2, 3 и два синих шара перенумерованных цифрами 1, 2. Сколько можно составить разноцветных упорядоченных "троек" из этих шаров?
Обозначим
множество белых шаров буквой
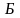 с элементами
с элементами
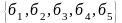 ,
множество красных шаров
,
множество красных шаров
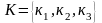 и множество синих шаров
и множество синих шаров
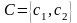 .
Тогда по правилу произведения число
разноцветных упорядоченных троек
вычисляется по формуле:
.
Тогда по правилу произведения число
разноцветных упорядоченных троек
вычисляется по формуле:
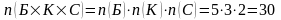 .
.
Пример 4. Сколько четырехзначных четных чисел можно составить из семи цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться.
Согласно
правилу произведения имеется
 способов составить четырехзначное
четное число из данных семи цифр.
способов составить четырехзначное
четное число из данных семи цифр.
Пример 5. Сколько можно образовать различных комбинаций, состоящих из одной буквы и трех цифр, если использовать 32 буквы и 10 цифр? Известно, что в комбинации цифры не могут повторяться, а нуль не может стоять на первом месте (в старшем разряде комбинации).
Обозначим
множество букв -
,
а множество цифр -
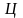 .
В каждой комбинации на первом месте
может стоять либо цифра, либо буква.
Поэтому рассмотрим два случая.
.
В каждой комбинации на первом месте
может стоять либо цифра, либо буква.
Поэтому рассмотрим два случая.
1. Если на первом месте стоит любая цифра из множества , кроме 0, то имеем три декартовых произведения вида:
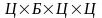
 имеем
имеем
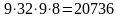 возможностей.
возможностей.
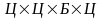 имеем
имеем
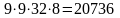 возможностей.
возможностей.
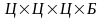 имеем
имеем
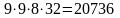 возможностей.
возможностей.
По
правилу суммы имеем
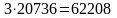 различных комбинаций.
различных комбинаций.
2.
Если на первом месте стоит буква, то
получим декартово произведение вида:
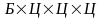 .
Число интересующих нас комбинаций равно
.
Число интересующих нас комбинаций равно
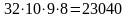 .
.
Общее
число комбинаций, таким образом, составит
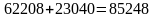 .
.
