Задача №4
В некотором государстве по закону подоходным налогом облагаются граждане, имеющие годовой доход не менее 5000 у.е. Считая, что доходы налогоплательщиков распределены по закону Парето с параметром
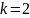 ,
найдите: 1) процент налогоплательщиков,
имеющих годовой доход более 10000 у.е., 2)
средний доход налогоплательщика,
3)процент налогоплательщиков, имеющих
годовой доход более 10000 у.е. в случае,
если закон изменится, и подоходным
налогом станут облагаться граждане с
доходом более 6000 у.е.
,
найдите: 1) процент налогоплательщиков,
имеющих годовой доход более 10000 у.е., 2)
средний доход налогоплательщика,
3)процент налогоплательщиков, имеющих
годовой доход более 10000 у.е. в случае,
если закон изменится, и подоходным
налогом станут облагаться граждане с
доходом более 6000 у.е.По данным ДПС скорости автомобилей в потоке распределены по нормальному закону. Известно, что 12% автомобилей движется со скоростью менее 60 км/ч, и 15% автомобилей движется со скоростью более 110 км/ч. Определите: 1) среднюю скорость автомобиля в потоке; 2) процент автомобилей, движущихся со скоростью более 100 км/ч; 3)процент автомобилей, движущихся со скоростями, отклоняющимися от средней скорости потока не более, чем на 15 км/ч; 4) границы интервала скоростей движения в соответствии с правилом «трех сигм».
Случайная величина распределена по закону Симпсона (правилу равнобедренного треугольника) на интервале [-2;2]. Определите: 1)плотность распределения случайной величины; 2) вероятность того, что случайная величина находится в интервале [1;2]; 3)математическое ожидание и дисперсию случайной величины.
Случайная величина
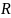 – расстояние от точки попадания до
центра мишени – распределена по закону
Релея c
плотностью
– расстояние от точки попадания до
центра мишени – распределена по закону
Релея c
плотностью
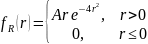 . Определите:
. Определите:
коэффициент
;
2) моду случайной величины, то есть точку
максимума ее плотности распределения;
3)
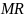 и
и
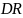 ;
4)вероятность того, что в результате
выстрела расстояние от точки попадания
до центра окажется меньше, чем мода.
;
4)вероятность того, что в результате
выстрела расстояние от точки попадания
до центра окажется меньше, чем мода.
Время безотказной работы устройства распределено по показательному закону с параметром распределения
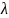 .
Найдите: 1) математическое ожидание
времени безотказной работы устройства,
2) вероятность того, что данная случайная
величина примет значение меньшее, чем
ее математическое ожидание.
.
Найдите: 1) математическое ожидание
времени безотказной работы устройства,
2) вероятность того, что данная случайная
величина примет значение меньшее, чем
ее математическое ожидание.Модуль скорости молекулы газа является случайной величиной
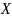 ,
распределенной по закону Максвелла:
,
распределенной по закону Максвелла: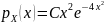 ,
если
,
если
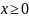 .
Найдите
,
.
Найдите
,
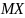 ,
,
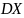 .
.Случайная величина имеет распределение Коши c плотностью
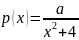 .
Найдите
.
Найдите
коэффициент
,
функцию распределения
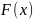 ,
медиану распределения, вероятность
нахождения случайной величины в интервале
,
медиану распределения, вероятность
нахождения случайной величины в интервале
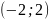 .
Определите,
.
Определите,
существуют ли математическое ожидание и дисперсия данной случайной величины?
Случайная величина имеет распределение Лапласа с плотностью
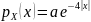 .
.
Определите
коэффициент
,
функцию
распределения ,
и
.
,
и
.
Случайная величина распределена на интервале (-3;3). График функция плотности на этом интервале представляет собой полуэллипс. Найдите функцию плотности, функцию распределения этой случайной величины, ее математическое ожидание и дисперсию.
Диаметр выпускаемой детали – случайная величина, подчиненная нормальному закону распределения с математическим ожиданием 6 см и с.к.о. 0,7 см. Определите вероятности событий: 1) случайно отобранная деталь имеет диаметр от 5,5 до 6,8 см: 2) отклонение диаметра от математического ожидания составляет не более 0,3 см. В каких границах должна быть величина диаметра, чтобы вероятность не выйти за эти границы составила 0,97?
Плотность распределения абсолютной величины скорости молекулы массой задается распределением Максвелла
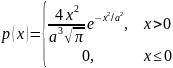 ,
,
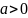 .
.
Определите среднюю скорость молекулы и среднюю кинетическую энергию.
Плотность распределения случайной величины
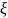 имеет вид:
имеет вид:
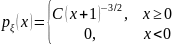 .
Найдите
константу
,
.
Найдите
константу
,
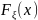 ,
,
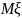 ,
,
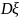 и
и
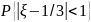 .
.
Дана функция распределения
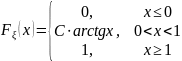 .
Найдите
константу
,
и
.
.
Найдите
константу
,
и
.Время безотказной работы батареи аккумуляторов постоянного тока имеет нормальное распределение с математическим ожиданием 30 часов и с.к.о. 4 часа. Определите: а) какова вероятность безотказной работы батареи в течение 25 часов? б) когда необходимо заменить батарею аккумуляторов, чтобы гарантировать, что вероятность появления отказа до момента замены не превышает 10 %?
Известно, что время безотказной работы элемента распределено по показательному закону со средним временем работы 1000 часов. Найдите дисперсию времени службы элемента и вероятности событий
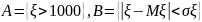 .
.Известно, что диаметр шарика для подшипников является случайной величиной, распределенной по нормальному закону. Браковка шарика происходит следующим образом: если шарик не проходит через отверстие диаметром 2,5 мм, но проходит через отверстие диаметром 3 мм, то его размер считается приемлемым. Если какое-либо из этих условий не выполняется, то шарик бракуется. Известно, что средний размер шарика равен 2,75 мм, а брак составляет 10% от выпуска. Определите с.к.о. диаметра шарика.
Случайная величина , распределенная равномерно на некотором интервале
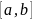 ,
имеет числовые характеристики
,
имеет числовые характеристики
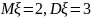 .
Найдите
и постройте ее график.
.
Найдите
и постройте ее график.
Плотность распределения СВ имеет вид
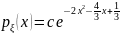 .
Найдите
.
Найдите
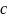 ,
,
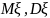 ,
,
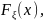
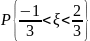 .
.Случайная величина имеет плотность распределения
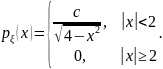 Найдите: а) значение параметра
;
б) функцию распределения
и постройте ее график; в) вероятность
Найдите: а) значение параметра
;
б) функцию распределения
и постройте ее график; в) вероятность
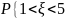 }.
}.Число неисправностей, обнаруженных при техническом осмотре автомобиля, распределяется по закону Пуассона с параметром
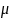 .
Если неисправностей не обнаружено, то
технический осмотр продолжается в
среднем 2 часа. Если обнаружена одна
или две неисправности, то на устранение
каждой из них тратится в среднем еще
полчаса. Если обнаружено больше двух
неисправностей, то машина ставится на
профилактический ремонт, где она
находится в среднем 4 часа. Определить
закон распределения времени
.
Если неисправностей не обнаружено, то
технический осмотр продолжается в
среднем 2 часа. Если обнаружена одна
или две неисправности, то на устранение
каждой из них тратится в среднем еще
полчаса. Если обнаружено больше двух
неисправностей, то машина ставится на
профилактический ремонт, где она
находится в среднем 4 часа. Определить
закон распределения времени
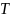 нахождения
машины на стоянке технического
обслуживания и его математическое
ожидание.
нахождения
машины на стоянке технического
обслуживания и его математическое
ожидание.
Количество ошибок на странице, допускаемых машинисткой при наборе, распределено по закону Пуассона. Известно, что вероятность того, что она допустит хотя бы одну ошибку, равна 0,8647. Определите вероятность того, что на странице будет более двух ошибок; найдите наиболее вероятное количество ошибок в документе, содержащем 5 страниц.
Время исправной работы стеклоочистителя подчинено гамма-распределению с параметрами
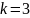 и
и
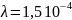 1/час. Определите вероятность безотказной
работы изделия в течение 10000 час, процент
стеклоочистителей, время работы которых
составит менее
1/час. Определите вероятность безотказной
работы изделия в течение 10000 час, процент
стеклоочистителей, время работы которых
составит менее
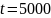 час, и среднюю наработку до первого
отказа.
час, и среднюю наработку до первого
отказа.Наработка до отказа гидравлического цилиндра выключения сцепления имеет логарифмически-нормальное распределение с параметрами
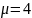 ,
,
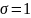 .
Определите вероятность безотказной
работы цилиндра в течение 150 часов.
Найдите медиану и моду этого закона
распределения
(медиана
- это такое значение
,
что
.
Определите вероятность безотказной
работы цилиндра в течение 150 часов.
Найдите медиану и моду этого закона
распределения
(медиана
- это такое значение
,
что
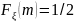 ,
мода- точка максимума плотности)
,
мода- точка максимума плотности)Наработка до отказа партии подшипников имеет 2-х параметрическое распределение Вейбулла с параметром износа
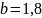 .
Вероятность безотказной работы партии
подшипников в течение наработки
.
Вероятность безотказной работы партии
подшипников в течение наработки
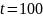 час равна
час равна
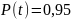 .
Найдите медиану и моду этого закона
распределения
(медиана
- это такое значение
,
что
,
мода- точка максимума плотности)
.
Найдите медиану и моду этого закона
распределения
(медиана
- это такое значение
,
что
,
мода- точка максимума плотности)Наработка на отказ изделия подчинена закону Рэлея с параметром
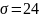 .
.
Определите значение средней наработки на отказ и вероятность безотказной работы в течение 40 часов.
В некотором государстве по закону подоходным налогом облагаются граждане, имеющие годовой доход не менее 10000 у.е, причем известно, что средний доход налогоплательщика составляет 30000 у.е. Считая, что доходы налогоплательщиков распределены по закону Парето, найдите: 1) процент налогоплательщиков, имеющих годовой доход мелее 20000 у.е., 2)процент налогоплательщиков, имеющих годовой доход больше среднего, 3) такой уровень дохода , что только у 10% налогоплательщиков доход выше .
Число элементарных частиц, зарегистрированных счетчиком за секунд, подчиняется закону Пуассона и составляет в среднем 4,5. Найдите вероятности следующих событий: 1) за
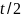 секунд не будет зарегистрировано ни
одной частицы, 2) за 2
секунд будет зарегистрировано не менее
9 частиц.
секунд не будет зарегистрировано ни
одной частицы, 2) за 2
секунд будет зарегистрировано не менее
9 частиц.Случайная величина подчиняется логистическому закону распределения с плотностью с параметрами
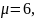
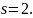 Найдите
математическое ожидание
Найдите
математическое ожидание
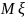 и
и
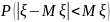 .
.Плотность распределения абсолютной величины импульса молекулы массой задается распределением Максвелла
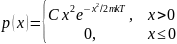 ,
,
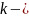 постоянная
Больцмана,
-
термодинамическая температура.
Найдите постоянную
постоянная
Больцмана,
-
термодинамическая температура.
Найдите постоянную
и среднее значение абсолютной величины импульса.
Плотность распределения СВ имеет вид
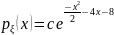 .
Найдите
,
,
.
Найдите
,
,
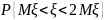 ,
,
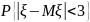 .
.
Приложение.
Интеграл
Пуассона
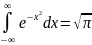
Распределе ние
|
Вероятности/ Плотность |
Распределение
|
Плотность |
1. Пуассона |
|
7. Логарифмически нормальное |
|
2. Геометри- ческое |
|
8. Гамма- распределение |
|
3. Биноми- альное |
|
двухпараметрическое
|
- интенсивность отказов;
|
4. Гипергео- метрическое |
|
10. Показательное |
|
5. Парето |
|
11. Релея |
|
6. Максвелла |
|
12. Логистическое |
|

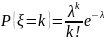
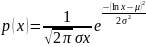 ,
,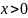
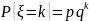
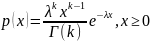
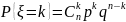
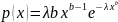 ,
,
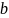 – параметр
формы
– параметр
формы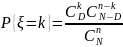
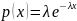 ,
,
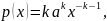
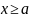
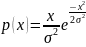 ,
,
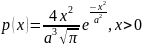
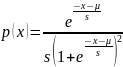 ,
,