Домашнее задание №1 «Элементарная теория вероятностей» Задача 1.

Сколькими способами можно раздать 18 различных предметов пяти участникам так, чтобы четверо получили по четыре предмета, а пятый – два предмета?
Сколько существует способов взять 10 карт из 36 так, чтобы среди них было 5 червей?
Найдите число различимых способов размещения 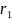одинаковых предметов одного вида и 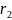одинаковых предметов другого вида по 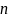ящикам.
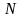человек, в том числе 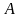и 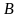, располагаются в ряд. Сколькими способами можно разместить и так, чтобы между ними было ровно 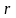человек?
Найдите число наборов длины 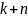, содержащие 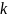раз букв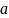у и раз букву .
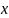Сколькими способами можно расселить 12 котят по 3 разным домикам, если в каждом домике помещается любое число котят?
Сколько кратчайших путей соединяют левый передний нижний и правый верхний задний углы куба 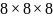? (Движение происходит по ребрам маленьких кубов).
Студенту необходимо сдать 4 экзамена в течение 10 дней. Сколькими способами может быть составлено расписание, если в один день можно сдавать не более одного экзамена?
Общество, состоящее из 5 мужчин и 10 женщин, разбивается случайным образом на пять групп по 3 человека. Сколько существует способов такого разбиения, чтобы в каждой группе оказался один мужчина?
В зале 120 мест. Сколько существует способов рассадить 50 человек так, чтобы определенные 10 мест оказались заняты?
Сколькими способами можно распределить 20 различных предметов между десятью лицами так, чтобы каждому досталось по два предмета?
Из полного набора костей домино (28 штук) случайным образом выбирается 7 костей. Сколькими способами можно выбрать эти кости так, чтобы среди них был хотя бы один дубль?
Сколько существует способов разделить колоду из 36 карт на две части так, чтобы в одной части полностью оказались все тузы и короли?
Найдите число различимых способов размещения 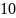одинаковых ручек и одинаковых карандашей по ящикам.
В урне имеется 10 белых шаров и 5 черных. Шары извлекаются по одному без возвращения. Сколько существует различимых по цвету последовательностей извлечения шаров?
Сколько существует способов рассадить за круглым столом 6 мужчин и 6 женщин, чтобы никакие два лица одного пола не оказались рядом?
Сколько способов выбрать на шахматной доске 7 полей так, чтобы никакие два поля не находились ни на одной вертикали, ни на одной горизонтали.
Сколько различных костей домино можно образовать, используя числа от 1 до ?
В ящике имеются шары трех цветов: 3 белых, 2 черных и 4 синих. Последовательно вынимается 5 шаров. Сколько различных цветовых последовательностей при этом может быть получено?
Сколько существует способов распределить различных предметов по 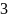неразличимым ящикам так, чтобы в каждом из них оказалось не менее трех предметов?
Сколько существует различимых способов построить 20 человек в ряд, чтобы трое друзей оказались рядом?
Сколько существует способов распределить одинаковых шаров по разным ящикам так, чтобы ни один ящик не оказался пустым?
Из полного набора костей домино (28 штук) случайным образом выбирается 5 костей. Сколькими способами можно выбрать эти кости так, чтобы среди них была хотя бы одна с шестеркой?
Сколько существует различных способов разделить колоду из 36 карт между четырьмя игроками так, чтобы каждому досталось по тузу?
Сколько различных «слов» можно получить, переставляя буквы в слове МАТЕМАТИКА?
Сколькими различными способами можно образовать хоровод для греческого танца «сиртаки» из 10 человек?
Группа из 12 дошкольников и одного Деда Мороза строится для хоровода вокруг новогодней елки. Сколькими различными способами можно образовать такой хоровод, чтобы мальчик Петя оказался рядом с Дедом Морозом?
Сколько различных палиндромов из 5 букв можно составить, если всего в алфавите имеется 10 букв?
Сколько различных «слов» можно получить, переставляя буквы в слове АБРАКАДАБРА?
Сколько существует различных способов взять 6 карт из 36 так, чтобы среди них были по 3 карты двух мастей?