Методика формування основних понять теми «Електромагнітні коливання»

Як показує педагогічний досвід, найбільші труднощі у учнів старших класів виникають при вивченні тих розділів курсу фізики, які пов’язані з електрикою і магнетизмом, тобто електродинамікою. Одна з тем, що входить до цього розділу, є тема «Електромагнітні коливання», яка в діючих підручниках подана у повному обсязі, але в досить стислій формі, фактично без математичних викладок і пояснення логіки формування понять чи виведення правил. Відтак такий підхід не забезпечує формування навчально-пізнавальної компетентності та розвиток інтелектуальних умінь учнів.

В даній темі розглядаються вільні електромагнітні коливання і автоколивання в коливальних контурах, а також вимушені коливання в електричних колах.

Всі ці питання мають велике значення для фізичної і політехнічної освіти учнів. На їх основі потім вивчаються електромагнітні хвилі з їх науковим і практичним використанням.

Для методики вивчення електромагнітних коливань особливо важливо:

1. використання аналогій механічних і електромагнітних коливань;

2. широке використання фізичного експерименту;

3. пояснення фізичної суті явищ на основі отриманих у 11 класі знань про електричне і магнітне поле та про електромагнітну індукцію.

Введення в фізику поняття поля Ейнштейн вважав самим важливим досягненням з часів Ньютона.

У ХVІІ-ХІХ ст. існували два погляди на фізичну картину світу – картезіанський і ньютонівський. Прибічники першого були послідовниками французького вченого Рене Декарта (Картезія) (1596-1650 рр.). Весь світ, за Декартом, заповнений матерією, яка знаходиться у вихровому русі. Тут відсутня пустота. При цьому рух матерії розуміється як механічний рух тіл. Це була теорія механічного матеріалізму. Наслідком цієї теорії було заперечення дії на відстані, тобто без використання середовища.

Ньютоніанці намагались пояснити всі явища природи, використовуючи формально-математично, механікою Ньютона. Вони були дуалістами і вважали, що в природі існує матерія і пустота, яка розділяє тіла, які взаємодіють на відстані. Але труднощі виникли у зв’язку з дослідом Ерстеда, який показав, що сила, яка діє між магнітним полюсом і елементом струму, є не центральною.

Із дослідів Роуланда слідувало, що електромагнітні сили залежать від швидкості руху електричних зарядів. А це вже ніяк не вкладалось в рамки класичної механіки.

Таким чином, намагання фізиків вивести всі закони електрики на основі законів Ньютона зустріли нездоланні труднощі. Потрібні були нові ідеї.

Ці ідеї висунув М. Фарадей. Відмінність у поглядах Фарадея характеризував Максвелл: «Фарадей своим мысленным оком видел силовые линии, проходящие по всему пространству там, где математики видели центры сил, притягивающие на расстоянии. Фарадей видел промежуточную среду там, где они ничего не видели, кроме расстояния. Фарадей искал сущность явлений в том, что в действительности происходит в среде, другие удовлетворялись тем, что находили эту сущность в способности действия на расстоянии, которою одарены электрические жидкости».

Максвелл розумів, що уявлення Фарадея про механічні властивості силових ліній поля, за допомогою яких продуктивно можна розв’язувати багато задач електрики і магнетизму, відображають по принципу аналогії якісь глибинні процеси і властивості відкритого Фарадеєм матеріального середовища.

Тому як метод своїх досліджень Максвелл і вибрав фізичну аналогію. Спираючись на ідеї Фарадея, Максвелл вперше ввів поняття поля як носія електромагнітної енергії, яка виявляється у дослідах.

Узагальнивши експериментальні факти, здобуті Фарадеєм, Максвелл представив їх у математичній формі:

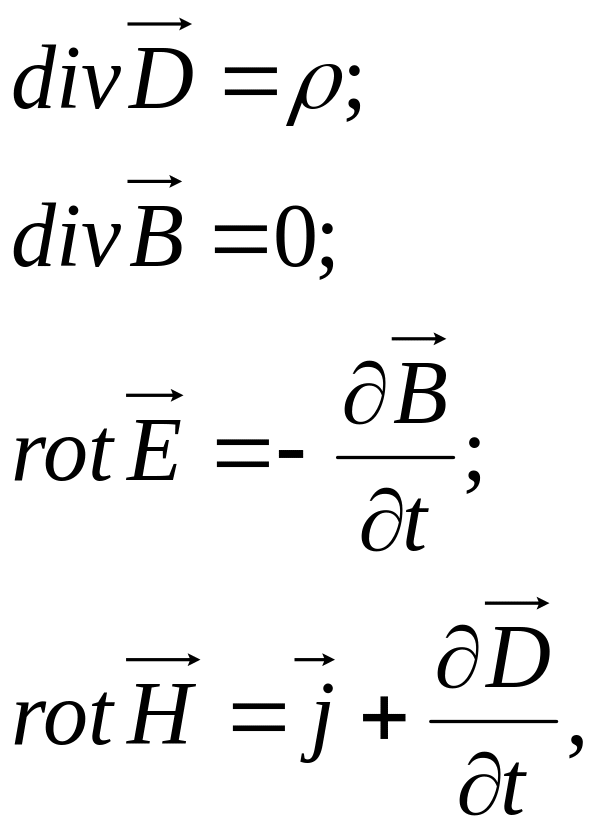
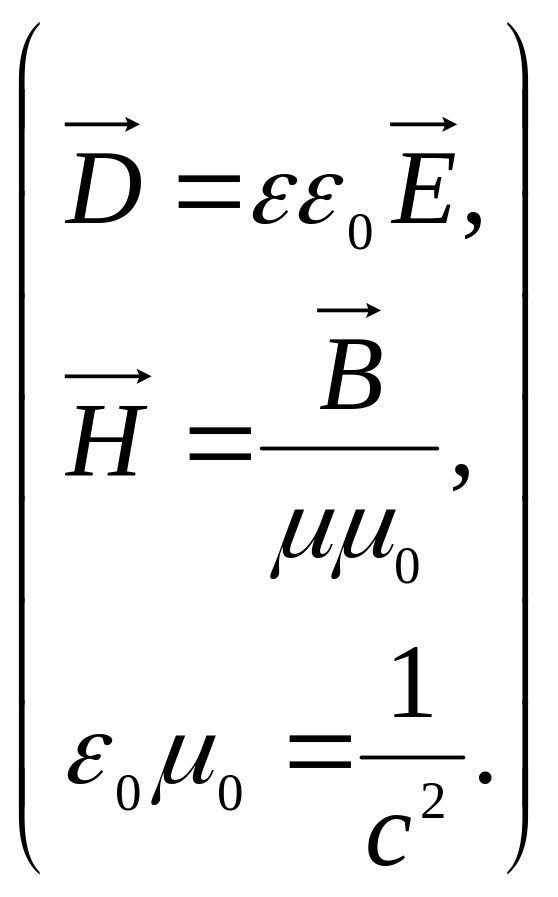
де і – вектори напруженості та індукції електричного поля; і – вектори індукції і напруженості магнітного поля; – густина електричного струму; – густина електричного заряду.

Максвелл висунув дві нові гіпотези: а) всяке змінне магнітне поле створює електричне поле, незалежно від того, є в ньому провідник чи немає. Це електричне поле він назвав «струм зміщення»; б) джерелом магнітного поля є не тільки струм провідності, а й «струм зміщення».

В основному якісно учні знайомляться з кожним рівнянням у школі.

Теорія Максвелла випередила свій час, сумнівними здавалися і її головні висновки, не підтверджені дослідами: передбачення струму зміщення, електромагнітних хвиль, електромагнітної природи світла, світлового тиску і ін. Являючись геніальним узагальненням експериментів, висновки Максвелла слугують для електромагнетизму такою ж основою, як закони Ньютона для механіки.

При вивченні властивостей електричного поля ми встановили, що воно має енергію і ця енергія може перетворюватися в інші види енергії.

Наприклад, при підключенні лампочки до зарядженого конденсатора вона спалахує, при цьому енергія електричного поля перетворюється у внутрішню енергію спіралі. Якщо підключити лампочку до котушки, то при розмиканні ключа лампочка теж спалахує, отже, магнітне поле теж має енергію, яка перетворюється в інші її види.

Аналогічний процес відбувається при вільних механічних коливаннях . Якщо енергії електрична і магнітна можуть перетворюватися в інші види, то – чи можуть відбуватися вільні коливання в електричному колі?

Структура з’ясування питання про електромагнітні коливання наступна:

Перший урок з теми «Електромагнітні коливання» є вступним. На цьому уроці корисно познайомити учнів з історією відкриття електромагнітних коливань і відновити у пам’яті основні відомості про явище електромагнітної індукції, закон , явище самоіндукції , після чого починають формувати уявлення про електромагнітні коливання.

Очевидно, що для отримання електромагнітних коливань необхідно мати електричне коло, в якому енергія електричного поля могла б перетворюватися в енергію магнітного поля і навпаки.

Оскільки магнітне поле зосереджене переважно в котушках, а електричне – в конденсаторах, найпростіше коло для утворення електромагнітних коливань має складатися з конденсатора й котушки. Таке коло називають коливальним контуром.

Одночасні періодичні зміни пов’язаних між собою електричного і магнітного полів називають електромагнітними коливаннями.

Щоб одержати електромагнітні коливання в контурі, достатньо зарядити конденсатор і замкнути його на котушку (рис. 1). При використанні батареї конденсаторів ємністю 60 мкФ для отримання коливань з періодом с необхідно взяти котушку з індуктивністю Гн. Таку індуктивність мають дві дросельні котушки з’єднані послідовно і розміщені на замкненому осерді від універсального трансформатора. Гальванометр приєднують до обмотки на 30 витків (червоної) намотаної зверху дросельної котушки (краще використовувати гальванометр від амперметра з опором 385 Ом, тому що цей опір близький до опору котушок і тому гальванометр буде «відбирати» від котушок найбільшу потужність.

К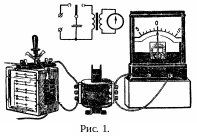 оливання розглядають в основному з енергетичної точки зору. Пояснюють при цьому аналогічність між механічною потенціальною енергією і енергією електричного поля конденсатора, кінетичну енергію спів ставляють з енергією магнітного поля, яка пов’язана з електричним струмом. Подальшою аналогією є аналогія енергетичних перетворень в конденсаторі і маятнику, краще пружинному. Щоб отримати вільні коливання в механічній коливальній системі, необхідно надати цій системі енергії від побічного джерела. У процесі коливань ця енергія періодично перетворюється з потенціальної в кінетичну і навпаки. Щоб коливальний контур вивести зі стану електричної рівноваги, також необхідно цій коливальній системі надати певної енергії. Найпростіше це зробити, зарядивши конденсатор. Заряджання конденсатора аналогічне відхиленню маятника від положення рівноваги, а енергія електричного поля зарядженого конденсатора аналогічна потенціальній енергії деформованої пружини або піднятого тягарця маятника.

Припустимо, що активний опір контуру дуже малий і ним можна знехтувати (ідеальний контур). Для наочності порівнюватимемо процеси в контурі з коливаннями тягарця на пружині.

Якщо конденсатор заряджений до різниці потенціалів , то його заряд дорівнює . У цьому стані енергія електричного поля максимальна і дорівнює , сила струму в контурі дорівнює нулю, магнітне поле в котушці індуктивності відсутнє (енергія магнітного поля дорівнює нулю). Цей стан (рис. 87, а) еквівалентний стану пружинного маятника, коли ми розтягнули пружину на , надали механічній коливальній системі потенціальної енергії , але тримаємо тягарець рукою, не даючи йому можливості рухатися.

Зрозуміло, що такий електричний стан в коливальному контурі не може залишатися незмінним, подібно тому, як пружина не може залишатися в деформованому стані після припинення дії зовнішньої сили. Конденсатор почне розряджатися і в колі потече струм. При цьому в котушці виникне потік магнітної індукції. Зростання цього потоку спричинить появу електрорушійної сили самоіндукції , яка дорівнює різниці потенціалів на пластинах конденсатора. Енергія електричного поля зарядженого конденсатора зменшується, а енергія магнітного поля котушки зростає. Цей процес аналогічний перетворенню потенціальної енергії деформованої пружини в кінетичну енергію руху тягарця.

Коли потенціали пластин зрівнюються (рис. 2, б), сила струму в котушці матиме максимальне значення, тому що немає причин для подальшого її зростання. З цього моменту сила струму зменшується. До того ж зменшується і магнітний потік, а тому в котушці виникає електрорушійна сила самоіндукції, яка прагне перешкодити зменшенню потоку індукції і сили струму. Таким чином, хоча конденсатор розрядився, струм у колі йде, заряджаючи конденсатор у зворотному напрямі. При цьому енергія магнітного поля котушки перетворюється в енергію електричного поля конденсатора. Так само й тягарець у положенні рівноваги має максимальну швидкість і за інерцією продовжує рухатися, стискаючи пружину; кінетична енергія руху тягарця перетворюється в потенціальну енергію пружини.

Коли сила струму зменшиться до нуля, конденсатор виявиться перезарядженим. На верхній пластині виникне негативний заряд, а на нижній — позитивний. Якщо втрат енергії в контурі немає, різниця потенціалів і заряд конденсатора дорівнюватимуть початковим, але з протилежним знаком. Електричний стан контуру в цей момент показано на рис. 2, в. Під час коливань тягарця цьому моменту відповідає зупинка його в крайньому верхньому положенні, коли потенціальна енергія максимальна.

Далі конденсатор починає знову розряджатися і в контурі виникає струм зворотного напряму, енергія електричного поля зарядженого конденсатора зменшується, а магнітного в котушці — зростає. В певний момент часу конденсатор розрядиться, сила струму досягне максимального значення і енергія магнітного поля буде максимальною (рис. 2, г). Це відповідає проходженню тягарцем положення рівноваги. Потім струм самоіндукції заряджатиме конденсатор, і коливальна система повернеться у вихідне положення. Далі весь процес повторюватиметься і в колі відбуватимуться електромагнітні коливання.

Разом з учнями встановлюємо величини-аналоги в механічних і електромагнітних коливаннях і оформлюємо їх у вигляді порівняльної таблиці.

Рис. 2.

Аналізуючи явища, які відбуваються у коливальному контурі приходимо до висновку, що у ньому виникають електромагнітні коливання. Спробуємо побудувати теоретичну модель цих коливань, проводячи аналогію з механічними коливаннями. Якщо знехтувати перетворенням електричної енергії у внутрішню енергію з’єднувальних провідників, то тоді повна енергія коливального контуру буде рівна:

(у будь-який момент часу).

Візьмемо похідну:

, якщо і _, то , або .

Якщо позначити , то одержимо: , яке аналогічне рівнянню , що є математичною моделлю гармонічних коливань. Розв’язком його є функція: .

Це дозволяє зробити ряд висновків:

1) у коливальному контурі виникають гармонічні коливання заряду і сили струму ;

2) власна частота гармонічних коливань у коливальному контурі і період коливань залежать лише від параметрів контуру, що підтверджується дослідом;

3) амплітуда коливань заряду і струму визначається початковою енергією контуру: .

Всі результати, отримані на основі теоретичної моделі, ілюструють за допомогою експерименту.

Для активізації пізнавальної діяльності учнів можна запропонувати учням скласти граф-схему «Вільні електромагнітні коливання» або заповнити її недостаючими відомостями:

Заповнення чи складання таких схем вимагатиме від учнів використання всіх розумових операцій, більш детального аналізу навчального матеріалу, встановлення причинно-наслідкових зв’язків, переконання у тому, що процеси у Всесвіті взаємопов’язані та взаємообумовлені, а також навчатимуть розрізняти причину і наслідок.

Генератор незатухаючих коливань (автоколивання). Електричні автоколивальні системи надзвичайно широко використовуються в сучасній техніці для одержання незатухаючих електромагнітних коливань

Зарядка конден-сатора q=		Е нергія електрич-ного поля we=		У колі виникає …………		Струм …………		У котушці виникає …………		С трум наростає поступово
Е нергія електр.поля переходить в …… we= wм=		Конден- сатор розрядився q= we=		Струм змен-шується		У котушці виникає …………, яка згідно з правилом Ленца …………		Струм припи-няється не митттєво		Конде-сатор … ………
Енергія wм= п ереходить в we=

в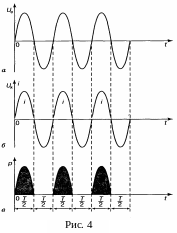 исокої частоти. Принцип дії цих систем значною мірою збігається з принципом дії механічних автоколивальних систем. Електрична автоколивальна система містить коливальний контур, підсилювач коливань і джерело електричної енергії (батарею). Між коливальним контуром і підсилювачем має існувати зворотний зв’язок – коливання з контуру передаються у підсилювач, підсилюються за рахунок джерела енергії і повертаються назад у коливальний контур. Дуже важливо, щоб коливання, які передаються від підсилювача в контур, збігалися за фазою з коливаннями у самому контурі.

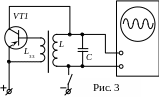
Існує багато автоколивальних систем як з електронними лампами, так і з транзисторами. На рисунку 3 показано спрощену схему електричної автоколивальної системи – автогенератора електромагнітних коливань на транзисторі. Коливальний контур приєднаний до джерела постійної ЕРС послідовно з транзистором. В емітер – базове коло транзистора – приєднана котушка, L_ЗЗ індуктивно пов’язана з коливальним контуром. Цю котушку називають котушкою зворотного зв’язку. Паралельно коливальному контуру увімкнутий електронний осцилограф для спостереження електромагнітних коливань. Генератор живиться від джерела постійної напруги.

Працює автогенератор на транзисторі так. Під час вмикання джерела живлення через транзистор проходить імпульс струму , який заряджає конденсатор контуру. В результаті в коливальному контурі виникають вільні електромагнітні коливання. Змінний струм, проходячи котушкою контуру, індукує на кінцях котушки зворотного зв’язку змінну напругу (рис. 4, а). Ця напруга подається на емітерний перехід транзистора. Внаслідок цього через транзистор проходять імпульси сили струму, тривалість яких залежить від режиму роботи транзистора. На рисунку 89, б показані імпульси сили струму, які тривають протягом півперіоду генерованих коливань. У перший півперіод коливання, коли емітерний перехід вмикається в прохідному напрямі, в колекторному колі транзистора йде струм. За напрямом він збігається зі струмом у котушці контуру. В результаті сила струму в котушці наростає і відбувається підзарядка конденсатора, тобто компенсуються втрати енергії в контурі.

У наступний півперіод, коли струм у контурі змінить напрям, на емітерний перехід транзистора з котушки зворотного зв’язку подається напруга протилежного знаку. Емітерний перехід вмикається в запірному напрямі, що призводить до зникнення струму в колекторі, тобто до закриття транзистора. Коливальний контур протягом півперіоду від’єднується від джерела напруги.

У наступний півперіод процес повторюється. Таким чином, роль транзистора зводиться до вмикання і вимикання джерела постійної напруги, за рахунок енергії якого у контурі підтримуються незатухаючі коливання. На рисунку 89, в заштриховані площі, пропорційні енергії, яка надходить у контур за кожен період коливань.

Може здатися, що з кожним періодом амплітуда коливань в контурі зростатиме нескінченно. Так би воно й було, якби сила струму емітера могла безмежно зростати у разі збільшення напруги на емітерному переході. Проте внаслідок насичення в транзисторі амплітуда коливань не може зростати до нескінченності, встановиться цілком певне її значення для даного режиму роботи генератора. Амплітуда автоколивань повністю визначається параметрами автоколивальної системи.

Щоб коливання, які почалися в контурі після замикання колекторного кола, перетворилися в незатухаючі, необхідно, щоб у колі емітера коливання збігалися за фазою з коливаннями в контурі. Адже вони можуть виявитися і в протифазі і тоді автоколивання не виникнуть.

Генератори незатухаючих коливань на транзисторах надійні в роботі, мають високий ККД, можуть працювати від малопотужних джерел живлення за надзвичайно низьких напруг на колекторі, дають змогу широко варіювати частоту, інтенсивність і форму коливань.

ВИСНОВОК: Таким чином, вміння підходити до аналізу коливальних процесів з єдиних позицій формується у учнів тільки тоді, коли вони вчаться будувати й аналізувати їх теоретичні моделі. Є і інший підхід при вивченні коливальних явищ різної природи: коли спочатку їх вивчають дослідним шляхом, а потім виконують теоретичний аналіз. По суті, ми маємо справу у цьому випадку з емпіричним рівнем формування знань. Але на жаль, в такому разі математичні методи аналізу коливань використовуються епізодично, не відіграють фундаментальної ролі, і, як наслідок, не сприяють розвитку теоретичного способу мислення учнів. З іншого боку, вибір методу викладання залежить від вчителя, його нахилів і, звісно, від навчальних здібностей учнів.

Література

1. Підручники з фізики для 11 класу.

2. Програма з фізики для 11 класу.

3. Методика преподавания физики в средней школе / Под ред. С.Е. Каменецкого и Л.А. Ивановой, – М.: Просвещение, 1987.

4. Методика преподавания физики / Под ред. В.П. Орехова, А.В. Усовой. Ч.2. – М.: Просвещение, 1977.

5. Орехов В.П. Колебания и волны в курсе физики средней школы.–М.: Просвещение, 1977.

6. Глазунов А.Т. и др. Методика преподавания физики в средней школе. – М.: Просвещение, 1989.

7. Методика навчання фізики у старшій школі: Навч. посібник / За ред. В.Ф.Савченка. – К.: ВЦ «Академія». – 2011. – 296 с.

Наші автори

Алєксєєв Артем Сергійович	магістрант кафедри фізики МНУ
Артюшкін Сергій	доцент ЧГУ ім. Петра Могили
Баран Олег Іванович	доцент кафедри математики та механіки МНУ
Бережецька Вікторія Генадіївна	студентка гр. 492 МНУ
Броницька Наталя Анатоліївна	доцент кафедри прикладної математики та ІКТ МНУ
Бугар Валентина Володимирівна	ст. лаборант кафедри фізики МНУ
Бузак Олег Олегович	студент гр. 492 МНУ
Васюра Кристина Олексіївна	студентка ПМ492 МНУ
Горошко Алла Аркадіївна	магістрант кафедри фізики МНУ
Гриза Олександр	студент МНУ
Запорожець Оксана	магістрант кафедри фізики МНУ
Іванніков Анатолій Володимирович	викладач кафедри фізики МНУ.
Іваннікова Олена Іванівна	зав. лаб. кафедри фізики МНУ.
Квачова Анастасія Олександрівна	магістрант кафедра фізики МНУ
Кравченко Оксана Григорівна	магістрант кафедри фізики МНУ
Кузнєцова Руфіна Сергіївна	студентка гр. ПМ 492 МНУ
Лавриньов Павло Григорович	доцент ЧДУ імені. П. Могили.
Лукьянчіков Сергій Дмитрович	ст. викладач кафедри ПМ та ІКТ МНУ
Манькусь Ірина Володимирівна	доцент кафедри фізики МНУ.
Мельник Віктор Анатолійович	КТН, доцент каф прикладної математики та ІКТ МНУ
Митрясова Олена	доцент ЧДУ імені. П. Могили.
Недбаєвська Людмила Степанівна	доцент кафедри фізики МНУ.
О вчинников Іван Петрович	доцент ЧДУ імені. П. Могили.
Олійник Олег Миколайович	доцент НАПКС, м. Симферопіль
Осадчук Михайло	магістрант кафедри фізики МНУ
Сущенко Станіслав Семенович	доцент кафедри фізики МНУ.
Тульский Володимир Володимирович	доцент кафедри прикладної математики та ІКТ МНУ
Федорінов Ігор	студент ЧДУ ім. П. Могили
Хейфець Ігор Михайлович	доцент кафедри фізики МНУ.
Ходякова Галина Вікторівна	доцент прикладної математики та ІКТ МНУ
Шатов Александр Алексеевич,	доцент ЧГУ ім. Петра Могили
Шилик Ольга Володимирівна	студентка гр. ПМ492 МНУ

53