3165 Министерство образования и науки российской федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра металлургических технологий
Математическая обработка результатов эксперимента
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим работам по курсу
«Основы научных исследований»
А.В. Карпов
Липецк
Липецкий государственный технический университет
2016
УДК 519.254 (07)
К265
Рецензент А.Н. Роготовский, канд. техн. наук, доц.
А.В. Карпов
К265 Математическая обработка результатов экспериментов [Текст]: методические указания к практическим работам по курсу «Основы научных исследований» / А.В. Карпов. – Липецк: Изд-во Липецкий государственный технический университет, 2016. – 23 с.
Рассмотрен способ расчета константы равновесия химических реакций. Приведены основные методы обработки статистических данных при помощи расчета парной корреляционной связи и множественного линейного регрессионного анализа. Уделено внимание методам планирования экспериментов.
Предназначены для студентов 2 курса металлургического института, направления 22.03.02 «Металлургия», изучающих дисциплину «Основы научных исследований»
Табл. 3. Библиогр. : 8 назв.
© ФГБОУ ВО «Липецкий
государственный технический
университет», 2016
Содержание
1. |
Расчет константы равновесия химических реакций ……………………... |
4 |
2. |
Статическая обработка данных пассивного эксперимента. Парная |
|
корреляционная связь ……………………………………………………….... |
8 |
|
3. |
Статическая обработка данных пассивного эксперимента. Множест- |
|
венный линейный регрессионный анализ …………………………………... |
11 |
|
4. |
Методы планирования эксперимента. Планы первого порядка ………... |
13 |
|
Библиографический список ……………………………………………….. |
16 |
|
Приложения ……………………………………………………………….... |
17 |
1. Расчет константы равновесия химических реакций
Равновесные соотношения указывают на пути протекания реакций, выявляют условия, термодинамически благоприятные для практической их реализации.
Подавляющее число процессов химических реакций металлургического передела протекают при постоянном или мало меняющемся давлении. В этом случае равновесие характеризуется энергией Гиббса. Энергия Гиббса – это часть внутренней энергии системы, которая может быть превращена в работу. Если исходные реагенты находятся в стандартном состоянии, т.е. их активности равны 1, изменение энергии Гиббса рассчитывается по уравнению (изотерма Вант-Гоффа):
(1.1)
где
– стандартное изменение энергии Гиббса,
–
универсальная газовая постоянная,
–
температура,
–
константа равновесия, выраженная через
равновесные активности.
Величина
связана со стандартным изменением
энтальпии
и энтропии
соотношением:
, (1.2)
По данному уравнению рассчитывается равновесие химических реакций и производится экспериментальное определение термодинамических свойств веществ.
Для
газов за стандартное принято состояние
вещества в виде идеального газа при
давлении 0,1013 МПа
(≈0,1 МПа,1 ат) и температуре 298 К. Для
такого состояния в термодинамических
таблицах имеются справочные данные о
стандартном изменении
и абсолютной энергии
.
Если в стандартном состоянии вещества находятся в жидком или твердом состоянии, термодинамические данные соответствуют их фиктивному состоянию в виде идеального газа.
Если в реакциях присутствуют простые вещества, то для них при всех температурах равны 0, но необходимо учитывать их абсолютную энтальпию.
Входящие в уравнение (1.1) активности идеального газа соответствуют их парциальным давлениям. Поэтому для реакции
Константа
равновесия (
)
определяется через парциальные давления
(
)
Тогда
(1.3)
Для
определения
реакций по уравнению (1.3) необходимо
рассчитать по формуле (1.2) величину
.
Для этого рассчитывают по табличным
данным для стандартных условий изменение
энтальпии
и энтропии
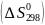как сумму для продуктов и исходных
компонентов с учетом величины и знака
стехиометрических коэффициентов:
Стехиометрические коэффициенты продуктов реакций берутся со знаком плюс (+), а исходных веществ – минус (-).
Тогда имеем:
(1.4)
Или после преобразования:
Тогда
(1.5)
По
уравнению (1.5) можно предсказать
температуру, при которой величина
будет достаточно большой, а по уравнению
(1.4) – приблизительно температуру начала
реакции, решив его относительно
при условии, что
.
Необходимо иметь в виду, что реакция
протекает слева направо, если изменение
энергии Гиббса имеет отрицательное
значение.
Выполненные по данной методике расчеты являются приблизительными, так как значения величин энтальпии и энтропии зависят не только от температуры, но и от теплоемкости, а последняя является функцией температуры, т.е.
Расчет термодинамических показателей реакции с учетом влияния температуры на изменение теплоемкости реагирующих веществ производится по методу Темкина-Шварцмана. Он основан на зависимости теплоемкости от температуры по уравнению
(1.6)
Коэффициенты уравнения определяются экспериментально. Причем достаточно первых трех членов уравнения (1.6), тогда:
Уравнение Темкина-Шварцмана для расчета имеет вид
где
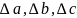– суммы коэффициентов уравнений
теплоемкости для реагентов и продуктов
реакции.
Значения
берутся также из справочных данных
термодинамических таблиц. При суммировании
значений
их величины умножаются на стехиометрические
коэффициенты. При этом продукты реакции
берутся со знаком плюс
,
а исходные реагенты – минус (-).
– интегралы Темкина-Шварцмана, зависят
только от температуры. Их значения
приведены в справочной литературе.
Если
давления при проведении реакции
возрастают, или их состояние близко к
насыщенному пару, газы перестают быть
идеальными и константу равновесия
необходимо определять через активности.
Поэтому константа равновесия для
реальных газов рассчитывается по
следующей методике. Введено понятие
летучести
.
Отношение летучести к парциальному
давлению называется коэффициентом
летучести
При давлении 1 ат
Тогда
Из данного уравнения получаем
где
(1.7)
Коэффициенты
летучести для реагирующих веществ
определяют исходя из приведенной
температуры
и приведенного давления
.
Для водорода
и
.
Значения
принимают по справочным данным. Для
каждого вещества находят значения
по табличным данным, т.е.
В приложениях приведены термодинамические характеристики некоторых веществ:
-
в приложении 1 -
;
- в приложении 2 – интегралы Темкина-Шварцмана;
-
в приложении 4 и 5 -
Алгоритм расчета константы равновесия для реальных газовых смесей:
1.
Рассчитывается
,
используя данные прил. 1;
2.
Рассчитывается
по методу Темкина-Шварцмана. Значения
интегралов
берутся из прил. 2, константы
– в уравнении теплоемкости из прил. 1;
3.
Определяется
из уравнения:
;
4.
Для каждого реагента рассчитывается
приведенная температура
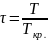и приведенное давление
.
Значения
берутся из прил. 1. По величинам
по данным прил. 4 и 5 определяются
коэффициенты летучести
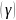для реагирующих веществ;
5.
По формуле (1.7) рассчитывается
;
6.
Определяется для данной реакции реальная
константа равновесия при заданной
температуре и давлении:
.
Задача 1. Рассчитать константу равновесия по методу Темкина-Шварцмана. Уравнение реакции, давление и температура ее протекания приведены в приложении 3.