1.3. Применение коэффициентов токораспределения для определения взаимных сопротивлений между отдельными источниками питания и точкой короткого замыкания

В практике расчетов токов КЗ часто возникает необходимость в определении взаимных сопротивлений между точкой КЗ и отдельными генераторами (рис. 1). Для этой цели можно использовать коэффициенты токораспределения. Если ток в точке КЗ условно принять за единицу, то, полагая все ЭДС ветвей равными по модулю и фазе, можно найти токи в ветвях схемы в долях от этой единицы. Значения долей тока в каждой ветви называются коэффициентами токораспределения и обозначаются С₁, С₂, …, С_n.

Рисунок 7 – Схема токораспределения

Следовательно, коэффициент токораспределения любой ветви численно равен току этой ветви, если суммарный ток в точке КЗ равен единице. Таким образом, коэффициенты токораспределения для генераторов характеризуют долю их участия в питании точки КЗ

По коэффициенту токораспределения Сi любого генератора и результирующему сопротивлению схемы относительно точки КЗ легко найти взаимное сопротивление между этим генератором и точкой КЗ как

_,

где Ż_ΣK для примера рис. 1 равно

.

С помощью коэффициентов токораспределения схема любой конфигурации довольно просто приводится к многолучевой звезде с вершиной в точке КЗ Общий ток в точке КЗ определяется в данном случае суммой токов отдельных ветвей, в которых учитывается влияние изменения величин и фаз отдельных ЭДС.

Коэффициенты токораспределения используют и тогда, когда необходимо найти величину тока, протекающему по любому элементу схемы к точке КЗ Для этого достаточно найти коэффициент токораспределения для данного элемента C_i и умножить его на суммарный ток в точке КЗ

_.

Коэффициенты токораспределения параллельных ветвей

Если имеется ряд параллельных ветвей, то коэффициенты токораспределения этих ветвей обратно пропорциональны их сопротивлениям. Коэффициент токораспределения любой из параллельных ветвей C_i так относится к суммарному коэффициенту токораспределения этих ветвей C₀, как общее сопротивление всех параллельных ветвей - к сопротивлению данной ветви Z_i , т.е.

.

Для примера рис. 7 при ( ); :

;

;

.

Коэффициенты токораспределения в сторонах треугольника по коэффициентам токораспределения в лучах звезды

Коэффициенты токораспределения С1, С2, С3 в лучах звезды, которые являются известными при КЗ в точке К, показаны на рисунке 8.

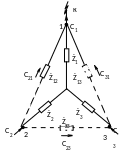
Рисунок 8. Рисунок 9.

Пунктирными линиями показан треугольник сопротивлений Ż₁₂, Ż₁₃, Ż₂₃, который в процессе преобразования схемы был заменен эквивалентной звездой с сопротивлениями Ż₁, Ż₂, Ż₃. Для определения коэффициентов токораспределения в сторонах треугольника достаточно знать напряжение, приложенное к каждой из сторон.

Поскольку коэффициенты С_i распределяются в элементах системы как токи, то, решив три уравнения Кирхгофа, искомые коэффициенты определятся как

; ; .

Если значение С₂₃ отрицательно, это указывает на то, что ток течет от узла 3 к узлу 2.

Коэффициенты токораспределения в лучах звезды по коэффициентам токораспределения в сторонах треугольника

Допустим, что коэффициенты токораспределения С₂₁, С₃₁, С₂₃ в сторонах треугольника известны (рис. 9).

Используя первый закон Кирхгофа, найдем:

С₁ = С₂₁+С₃₁; С₂ = С₂₁+С₂₃; С₃ = С₃₁-С_23.