
- •1.Обгрунтування необхідності згущення опорної їснуючої сітки
- •2. Вибір способу
- •3. Визначення висот знаків та типів центрів
- •4.Вибір інструментів та спосіб вимірування
- •Будова теодоліта 2т30.
- •Вимірювання напрямків способом кругових прийомів.
- •5.Визначення планових координат пунктів опорної сітки
- •6.Створення висотної основи на кар‘єрі.
- •Технічне нівелювання способом із середини нівеліром н-3.
5.Визначення планових координат пунктів опорної сітки
Пряма кутова засічка
Прямою кутовою засічкою називають побудову на місцевості, в якій координати невідомого пункта Р визначають за координатами вихідних пунктів А і В і виміряними на цих пунктах кутами А і В (рис. 1.1)
|
|
Рис.1.1 Пряма одноразова засічка |
Рис.1.2 Пряма багаторазова засічка |
Засічку, показану на рис.1.1 називають прямою одноразовою засічкою.
В прямій одноразовій засічці відсутній контроль виміряних кутів, отже координати пункта Р також визначаються безконтрольно.
На рис.1.2 показаний випадок, коли пункт Р визначається за координатами трьох вихідних пунктів А,В і С і виміряними на цих пунктах кутами А1, В1 та А2, В2.
Таку засічку називають багаторазовою.
Пряма багаторазова засічка фактично являє собою дві одноразових засічки, які можуть бути розв’язані окремо, а отже, координати пункта Р будуть знайдені з контролем.
Формули для обчислення координат пункта Р із прямої одноразової засічки
Отримаємо формули для визначення координат пункта Р із прямої одноразової засічки.
З трикутника АВР запишемо:
|
|
(5) |
де дирекційний кут
|
|
(6) |
причому
дирекційний кут
 АВ
може бути знайдений за координатами
пунктів А і В з розв’язання оберненої
геодезичної задачі.
АВ
може бути знайдений за координатами
пунктів А і В з розв’язання оберненої
геодезичної задачі.
Підставимо (5) в (6).
Матимемо
|
|
(7) |
або
|
|
(8) |
Але
|
|
(9) |
|
|
(10) |
Підставимо вирази (9) і (10) в (8).
Отримаємо
|
|
(11) |
В правих частинах виразів (11) винесемо sinA за дужки:
|
|
(12) |
Замінимо
вираз ![]() через
ctgA і отримаємо
через
ctgA і отримаємо
|
|
(13) |
З трикутника АВР за теоремою синусів запишемо
|
|
(14) |
Скористаємося формулою для синуса суми кутів:
![]() .
.
Домножимо обидві частини цієї рівності на sinA
![]() .
.
Поділимо чисельник і знаменник правої частини на sinBsinA. Отримаємо
|
|
(14) |
Підставимо
значення  в
формули (13):
в
формули (13):
|
|
(15) |
звідки остаточно запишемо
|
|
(16) |
Формули (16) називають формулами котангенсів або формулами Юнга.
Звертаємо увагу, що формули (16) можна застосовувати у випадку, коли пункт А — лівий, пункт В — правий (див. рис. 1.1) та коли між пунктами А і В існує видимість.
Задача передбачає визначення координат точки, з якої здійснюються спостереження трьох пунктів з відомими координатами, в ході спостережень вимірюються кути між напрямками з точки стояння на пункти, що спостерігаються (рис. 2).
|
Відомі: (xА , yА), (xБ , yБ), (xС , yС)
Визначені в ході вимірювань: βАБ, βБС
Знайти: (xР , yР)
Рішення:
1. Рішення задачі виконується за формулою Праніс-Праневіча.
![]()
2. Контроль різностей координат:

3. Розраховуємо прирости координат точки Р відносно точки Б:
![]() ;
;
![]() ;
;
![]() .
.
4. Визначаємо координати точки Р:
![]() ;
;
![]() .
.



 ,
,
 .
. .
. .
. .
.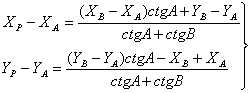 .
. .
. Рисунок
2. Схема оберної кутової засічки
Рисунок
2. Схема оберної кутової засічки