6.9. Поперечно – обтекаемые пучки труб

Сопротивление пучков труб при поперечном обтекании следует рассматривать как сумму сопротивлений трения, обусловленного вязкостными силами, и сопротивления формы, связанного с отрывом пограничного слоя и последующим образованием вихрей. Схема отрывного течения представлена на рис. 9.

Рисунок 2.

На рисунке показаны эпюры продольной составляющей средней скорости. Непосредственно за телом расположена зона возвратных токов, ограниченная поверхностью, на которой продольная компонента усредненной скорости равна нулю. Скорость обратных токов может достигать 60% от скорости основного потока. Граница между областью прямых и обратных токов проходит по линии abc. Линия ad отделяет ядро потенциального потока от вихревой области.

Для плохо обтекаемого тела силы трения незначительные. Например, для круглого цилиндра при Re = 10⁴ сила сопротивления трения составляет около 2% от полной силы лобового сопротивления. В гладкотрубном пучке при поперечном обтекании потоком сопротивление трения составляет несколько процентов от общего гидравлического сопротивления. При этом коэффициент местного сопротивления определяется по формулам ВТИ.

Для шахматных пучков:

при

; (145)

при

. (146)

В формулах (75) и (76) α = s₁/d – относительный поперечный шаг и S₂^' - диагональный шаг шахматного пучка; d – диаметр трубы; Z – число рядов труб в пучке.

Для коридорных пучков:

при

; (147)

при

. (148)

Показатель степени m в формулах (147) и (148) может быть вычислен следующим образом:

при b ≥ 1,24

;

при b < 1,24

.

В этих уравнениях a = S₁/d и b = S₂/d – относительный поперечный и продольный шаги в коридорных пучках. В формулах (145) – (148) число Эйлера

,

где υ – средняя скорость потока в узком сечении пучка; ρ – плотность теплоносителя.

Указанные формулы справедливы для 6·10³ < Re < 6·10⁴ и 0,25 < (1 – d/ )/(a – 1) < 2,5 для шахматных пучков и 0,2 < (b – 0,8)/(a – 1) < 6,5 для коридорных пучков.

В случае неизотермических условий можно использовать зависимость (145) – (148), принимая теплофизические свойства теплоносителя по средней температуре потока в пучке. При больших числах Рейнольдса с изменением температуры влияние изменяющихся физических параметров в пограничном слое на сопротивление незначительно, так как доля сопротивления поверхностного трения мала по сравнению с полным сопротивлением.

При небольших числах Re в потоках вязких жидкостей влияние изменяющихся физических свойств на сопротивление при неизотермических условиях учитывается согласно зависимости

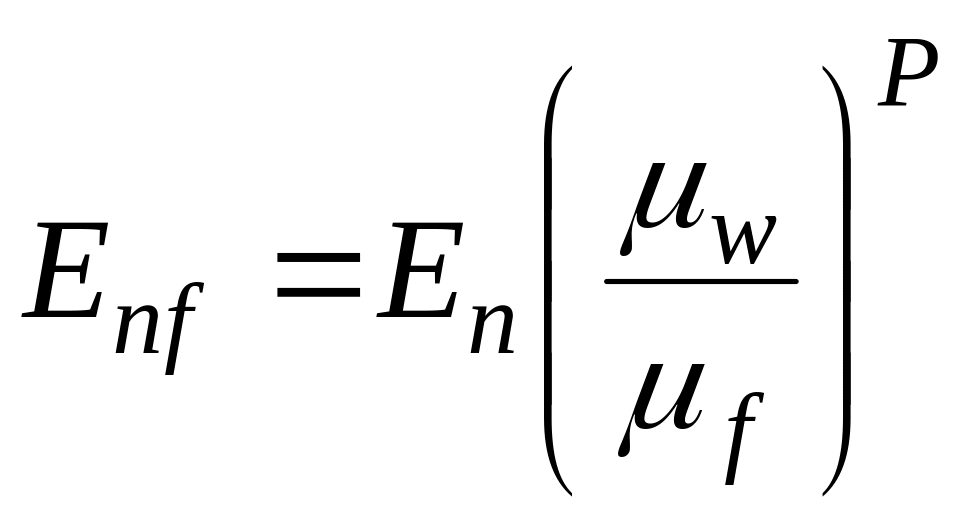, (149)

где E_nf – число Эйлера при нагревании или охлаждении жидкости;

E_n – число Эйлера в изотермических условиях; μ_w, μ_f – динамический коэффициент вязкости жидкости при температуре стенки и потока соответственно. Показатель Р при μ_w/μ_f определяется по табл. 15.

Таблица 15

Режим	Re
	10	20	40	80	100	200	400	800	1000
Нагрев	0,15	0,12	0,09	0,06	0,05	0,03	0,02	0,01	0,00
Охлаждение	0,27	0,22	0,18	0,14	0,12	0,08	0,05	0,03	0,02

Для расчета сопротивления пучков наиболее удобно применять номограммы, которые составлены на базе экспериментальных данных для потоков разных жидкостей

При разработке номограмм для коридорных пучков труб за основу принималось сопротивление пучков с расположением труб по вершинам квадрата. Определяющим служил продольный шаг. Для пучков с иными шагами в зависимости от их величины и числа Re введена графически определяемая поправка.

При разработке номограмм для шахматных пучков труб за основу принимались пучки с расположением труб по вершинам равностороннего треугольника. Для пучков с иным расположением труб в основной график, учитывающий влияние поперечного шага, также введена поправка в зависимости от шагов числа Re.

На рис. 10 приведены номограммы для расчета среднего коэффициента

Рисунок 3.

сопротивления многорядных коридорных и шахматных пучков труб, отнесенного к одному ряду. Номограммы составлены относительно коэффициента сопротивления ξ = 2E_И.

При определении по этим номограммам гидравлического сопротивления многорядного пучка труб следует пользоваться формулой

, (150)

где υ – скорость в наименьшем проходном сечении, а число Re составляется по этой скорости и диаметру трубы. При определении коэффициента сопротивления ξ для коридорных пучков с любым расположением труб вначале определяется член ξ/χ по продольному относительному шагу b, а затем по вспомогательному графику – множитель χ, после чего рассчитывается коэффициент сопротивления .

Коэффициент сопротивления шахматных пучков получается таким же путем, только определение величины ξ/χ, как отмечено на номограмме, ведется на основе поперечного относительного шага a.

Гидравлическое сопротивление пучков, трубы в которых наклонены к направлению потока под углом, как и пучков с поперечно-обтекаемыми трубами, зависит от конфигурации пучков, величины относительных шагов, числа Re, угла наклона труб и других факторов. Поэтому для расчета их сопротивления применяются те же зависимости, что л в случае поперечно-обтекаемых пучков труб с учетом угла потока к трубам β:

, (151)

где С_β – коэффициент, учитывающий угол наклона труб к потолку. Величина С_β определяется по табл. 16.

Таблица 16

Тип пучка	Угол наклона труб к потоку βº
	90	80	70	60	50	40	30	25
Шахматный	1	0,98	0,92	0,83	0,71	0,57	0,41	0,35
Коридорный	1	0,97	0,87	0,76	0,63	0,48	0,34	0,27

Уменьшение сопротивления пучков труб с β < 90° обусловлено изменением обтекания трубы и изменением соотношения составляющих сопротивления – трения и давления. С уменьшением β доля сопротивления трения увеличивается, хотя сопротивление давления остается существенным вплоть до минимального значения β = 25°.