Synchrone und asynchrone Schaltwerke
Schaltnetze |
Schaltwerke |
Die Ausgabe hängt lediglich von den Werten der Eingangsvariablen zum gleichen Zeitpunkt ab |
Die Ausgabewerte hängen auch von Belegungen der Eingangsvariablen zu vergangenen Zeitpunkten ab |
Moore |
Mealy |
Berechnung: Nur Zustand |
Berechnung: Zustand und Eingabe |
Änderungen des Ausgangs nur nach Zustandsänderung am Ausgang verfügbar (synchron: zum neuen Takt) |
Wegen Durchgriff des Eingangs kann sich der Ausgang sofort ändern, also unabhängig von der Zustandsänderung (synchron: vor neuen Takt) |
Synchrone Schaltwerke |
Asynchrone Schaltweke |
|
Werden alle Zustandsspeicher von einem oder mehreren zentralen Synchronisationssignal(en) T (Takt) gesteuert |
Anderfalls |
|
Synchronisation |
||
Pegelgesteuert (Latches) |
Flankengesteuert |
|
Die Eingänge wirken sich nur auf den Zustand aus, wenn der Takt z. B. den Wert 1 hat |
Nur während der positiven (0 1) (negativen) (1 0) Taktflanke werden die Eingabewerte in den Speicher übernommen |
|
Flipflops (taktgesteuerte Zustandsspeicher) |
|||
RS |
D |
JK |
T |
r = s = 1 verboten |
r = s = 1 Verbot wird immer beachtet |
r = s = 1 Ausgang komplementiert
|
Eingang = 1 Ausgang komplementiert, sonst speichern |
Schaltwerkanalyseschritte:
1. Ansteuergleichungen der Flipflops bestimmen.
2. Kodierte Ablauftabelle (Übergangstabelle) aufstellen.
3. Automatengraphen entwickeln. Rechnerarithmetik und Codes
2 |
8 |
10 |
16 |
Zahl → Zahl in ZKPL Dualwert bestimmen, negieren, +12 |
1 Ziffer = 3 Bits |
Zahl div n = zi (R = …) |
1 Ziffer 16 = 4 Bits |
Zahl2(Zkpl) → Zahl10 Zahl2 negieren, aus diesem Zahl den Dezimalwert bestimmen, +110, Vorzeichen |
|
zi div n = zi+1 |
|
Ieee-p 754
minreal |
0000 0000 1000 0000 ··· 0000 = (1,0···00)2 · 2-126 |
maxreal |
0111 1111 0111 1111 ··· 1111 = (1,11···11)2 · 2127 |
+∞ |
0111 1111 1000 0000 ··· 0000 |
-∞ |
1111 1111 1000 0000 ··· 0000 |
NaN |
0111 1111 1000 0000 ··· 0001 |
+0 |
0000 0000 0000 0000 ··· 0000 = (0,0···00)2 · 2-126 |
-0 |
1000 0000 0000 0000 ··· 0000 = (0,0···00)2 · 2-126 |
X = ± Mantisse · bExponent
Exponent = Charakteristik – 127
Normalisierung: Erstes Bit der Mantisse (die implizite 1) steht vor dem Komma
Beispiel:
Z = (-1)0·24·(1,1100 0000 ... 0000)2 = + (1 + 0,5 + 0,25)10 ·24 = 28
0
100
0001 1110 0000 0000 0000 0000 0000
Hamming-Code:
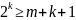
k = Anzahl zusätzlichen Korrekturbits Alle ki gleich Null -> Kein Fehler
m = Zahl der Datenbits k5k4k3k2k1 als Dualzahl zeigt die Position des Fehlers
M
IMA-Architektur
Befehlsabarbeitung: Lese-Phase -> Dekodierphase -> Ausführungsphase.
3 Taktzyklen für Lese- und Schreibzugriffe.
Anzahl der ALU-Operationen: 8
Maximale Anzahl der MIMA-Befehle: 31
Beim Extrahieren aus einem 24-Bit breiten Datenbus werden höchstwertigen 4 Bits abgeschnitten.
Lese-Phase 1.Takt: IAR -> SAR; IAR -> X; R=1 2.Takt: Eins -> Y; R=1 3.Takt: ALU auf Addieren; R=1 4.Takt: Z -> IAR 5.Takt: SDR -> IR |
LDV 7. Takt: IR -> SAR; R = 1 8. Takt: R = 1 9. Takt: R = 1 10. Takt: SDR -> Akku |
EQL 7. Takt: IR -> SAR; R = 1 8. Takt: Akku -> X; R = 1 9. Takt: R = 1 10. Takt SDR -> Y 11. Takt ALU auf 111 12. Takt Z -> Akku |
OR 7. Takt: IR -> SAR; R = 1 8. Takt: Akku -> X; R = 1 9. Takt: R = 1 10. Takt: SDR -> Y 11. Takt: ALU auf OR 100 12. Takt: Z -> Akku |
LDC 7. Takt: IR -> Akku |
JMP 7. Takt: IR -> IAR |
ADD 7. Takt: IR -> SAR; R = 1 8. Takt: Akku -> X; R = 1 9. Takt: R = 1 10. Takt SDR -> Y 11. Takt ALU auf ADD 12. Takt Z -> Akku |
STV 7. Takt: Akku -> SDR 8. Takt: IR -> SAR, W=1 9.Takt: W=1 10. Takt: W=1
|