УДК 599.722

Динамика составного космического аппарата с подвижным устройством в трёхосном кардановом подвесе

© А.В. Алексеев¹, А.В. Дорошин¹, А.В. Ерёменко¹,

Д.А. Ивакин², М.М. Крикунов¹, М.О. Недовесов¹, А.В. Филатов².

1Федеральное государственное автономное образовательное учреждение высшего образования «Самарский национальный исследовательский университет имени академика с.П. Королева»,

2Акционерное общество «Ракетно-космический центр “Прогресс”»

doroshin@ssau.ru, huntergalaxy@bk.ru, filatov_artem@rambler.ru

КОСМИЧЕСКИЙ АППАРАТ, ДВИЖЕНИЕ ВОКРУГ ЦЕНТРА МАСС, ПОДВИЖНОЕ УСТРОЙСТВО, КАРДАНОВ ПОДВЕС

Реферат. В работе моделируется движение космического аппарата (КА) переменной конфигурации, связанной с наличием внутри базового тела–носителя дополнительного твердого тела, закрепленного в кардановом подвесе. Внутреннее тело представляет собой подвижное устройство (ПУ), которое может представлять собой перенаправляемую антенну, либо рабочий элемент системы дистанционного зондирования. Математическая модель движения КА с ПУ строится на основе теорем об изменении кинетического момента и кинетической энергии системы. Моделирование пространственного движения составного КА осуществляется без ограничений на величины углов относительного движения подвижного устройства.

1. Введение

…сказать о предшествующих исследователях и их результатах…[xxx]

2. Математические модели

Рассмотрим механическую структуру составного КА со взаимосвязями и внутренними степенями свободы, приведённую на рисунке (рис.1).

Рисунок 1 – Структура составного КА с внутренними степенями свободы: 1 – корпус космического аппарата (несущее тело), тело 2 – подвижное устройство, установленное на кардановом подвесе

С_КАX_KAY_KAZ_KA – система координат, начало которой совпадает с центром масс составного КА, а оси параллельны главным центральным осям инерции корпуса (несущего тела) космического аппарата;

С_АX_AY_AZ_A – система координат, начало которой совпадает с центром масс несущего тела, а оси являются главными центральными осями инерции несущего тела;

O_KX_KY_KZ_K – cистема координат, начало которой совпадает с неподвижной точкой карданова подвеса;

C_tX_tY_tZ_t – система координат, начало которой совпадает с центром масс подвижного устройства, а оси являются главными центральными осями инерции подвижного оборудования;

OXYZ – кенигова неподвижная система координат;

Рассмотрим движение составного КА в системе координат С_КАX_KAY_KAZ_KA, которую будем именовать основной. Определим положения центров масс частей космического аппарата в основной системе координат (рис.1). Для центра масс составного КА справедливо соотношение:

, (1)

_где и – радиус-вектор центра масс в основной системе координат и масса подвижного оборудования, и – радиус вектор центра масс в основной системе координат и масса несущего тела, – радиус вектор центра масс всей составного КА в основной системе координат.

Запишем радиус-вектор центра масс составного КА в системе координат O_KX_KY_KZ_K, связанной с точкой крепления карданова подвеса, оси которой параллельны осям главной системы координат:

, (2)

где – матрица перехода от системы координат связанной с центром масс специального оборудования к основной системе координат, – неподвижная точка карданова подвеса(точка крепления карданова подвеса), – центра масс несущего тела, – центр масс подвижного оборудованиям.

Запишем выражения для определения радиус вектора центра масс несущего тела в основной системе координат С_КАX_KAY_KAZ_KA:

, (3)

где – радиус вектор центра масс несущего тела в системе координат связной с неподвижной точкой кардана. Радиус вектор центра масс подвижного оборудования для удобства дальнейших вычислений запишем в его собственной системе координат C_tX_tY_tZ_t:

, (4)

где - радиус вектор центра масс подвижного оборудования в системе координат связной с неподвижной точкой кардана, - матрица перехода от основной системы координат к системе координат связанной с центром масс специального оборудования C_tX_tY_tZ_t,

Запишем выражение кинетического момента несущего тела относительно собственного цента масс в основной системе координат С_КАX_KAY_KAZ_KA:

, (5)

где тензор инерции корпуса космического аппарата основной системе координат С_КАX_KAY_KAZ_KA, - вектор угловой скорости корпуса космического аппарата в основной системе координат С_КАX_KAY_KAZ_KA.

Для определения количества движения несущего тела в основной системе координат С_КАX_KAY_KAZ_KA запишем выражение для определения скорости центра масс несущего тела относительно общего центра масс в основной системе координат:

. (6)

В свою очередь выражение для определения количества движения в основной системе координат С_КАX_KAY_KAZ_KA примет вид:

. (7)

Запишем выражение для определения кинетического момента движения подвижного оборудования относительно собственного цента масс в системе координат связанной с центром масс специального оборудования C_tX_tY_tZ_t:

, (8)

где - тензор инерции подвижного оборудования в собственной системе координат C_tX_tY_tZ_t, - вектор угловой скорости подвижного оборудования в собственной системе координат C_tX_tY_tZ_t. Абсолютная угловая скорость подвижного оборудования в собственной системе координат будет складываться из относительной скорости и скорости несущего тела:

(9)

где – вектор угловой скорости специального оборудования относительно несущего тела.

Относительная угловая скорость ПУ определяется вращением карданова подвеса и будет иметь различный вид в зависимости от выбранной последовательности поворота кардана. Последовательность поворотов может быть разной. В рассматриваемом случае принята последовательность поворотов вокруг осей X Y Z. Тогда Компоненты угловой скорости кардана определяются следующими кинематическими уравнениями:

, (10)

где - проекции относительной угловой скорости на оси системы координат C_tX_tY_tZ_t, α, β, γ, - углы Крылова системы координат C_tX_tY_tZ_t относительно системы координат С_КАX_KAY_KAZ_KA.

Для определения количества движения подвижного оборудования в собственной системе координат C_tX_tY_tZ_t запишем выражение для определения скорости центра масс специального оборудования относительно общего центра масс в осях системы координат C_tX_tY_tZ_t:

. (11)

Выражение для определения количества движения подвижного оборудованиябудет иметь вид:

. (12)

Для построения динамических уравнений будем использовать теорему об изменении кинетического момента:

, (13)

_где - вектор главного кинетического момента движения составного КА, вычисленный относительно общего центра масс, - главный момент внешних сил, действующих на всю механическую систему, вычисленный относительно общего центра масс.

При отсутствии внешних сил, действующих на механическую систему, производная вектора кинетического момента движения составного КА будет равна нулю и, следовательно, вектор главного кинетического момента движения составного КА будет оставаться постоянным:

, (14)

(15)

Запишем уравнение (14) в векторном виде:

. (16)

Кинетические моменты движения составного КА, вычисленные относительно общего центра масс в системе С_КАX_KAY_KAZ_KA имеют вид:

, (17)

, (18)

. (19)

Подставим выражение (19) в выражение (16) и получим первые три уравнения движения составного КА в абсолютной системе координат:

. (20)

Для нахождения оставшихся трёх уравнений движения составного КА, описывающих внутренние степени свободы, применим теорему об изменении кинетического момента только к части подвижного оборудования:

, (21)

где - главный момент внутренних сил действующих на специальное оборудование, вычисленный относительно общего центра масс.

Уравнения (20) и (21) образуют систему динамических уравнений движения всей составного КА.

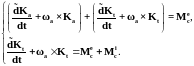(22)

Спроецировав уравнения (22) на оси системы координат связанной с осями несущего тела, получим шесть скалярных дифференциальных уравнений:

, (23)

где (i=1..6) - коэффициенты, определяющиеся производными компонентов угловых скоростей частей составного КА; (i =1..6) - коэффициенты, соответствующие гироскопическим моментам. Все указанные коэффициенты являются зависимыми от компонент угловых скоростей всех частей составного КА и от углов относительного перемещения подвижного оборудования. Перечисленные ранее коэффициентывведены в интересах компактной записи системы дифференциальных уравнений, так как запись системы уравнений в раскрытом виде является необозримой.

Кинетическая энергия составного КА выражается через сумму кинетических энергий вращательного и поступательного движения частей составного КА относительно общего центра масс:

, (24)

где -полная кинетическая энергия несущего тела, -полная кинетическая энергия подвижного оборудования.

При отсутствии моментов внешних сил полная кинетическая энергияTсоставного КА и модуль главного кинетического момента системы остаются постоянными (T=const, =const), поэтому численная проверка этих условий является критерием корректного интегрирования системы численными методами.