
Математическая модель
Начнем данный раздел с постановки задачи.
Постановка задачи
Рассмотреть одну из математических моделей эпидемии и реализовать ее на одном из языков программирования. Реализация помимо непосредственно модели должна содержать обучающую часть (пример и задача), краткую справку о модели и пример моделирования реальной ситуации.
Перейдем к решению поставленной задачи.
Sir-модель эпидемии
Для того чтобы успешно решать задачу математического моделирования эпидемического процесса, в любом случае, необходимо сформулировать ряд ограничений и предположений, в рамках которых будет работать модель. К подобным предположениям, к примеру, относятся предположения о характере заболевания, о структуре рассматриваемой популяции и некоторые другие. Так, для многих детских заболеваний, после перенесения которых вырабатывается стойкий (а, возможно, и пожизненный) иммунитет, представляется логичным разделить рассматриваемую группу людей на 3 класса:
те, кто восприимчивы к заболеванию
те, кто болеет в данный момент
те, кто переболел и приобрел иммунитет к заболеванию
Существуют общепринятые обозначения для упомянутых выше групп. Первая группа обозначается латинской буквой S(от англ.succeptible– восприимчивые), вторая –I(от англ.ill– больные), а третья –R(от англ.recovered– выздоровевшие). Именно по этой причине модель и получила названиеSIR-модель. Впервые эта модель была упомянута в трудах [1] британских ученых Kermack W.O. и McKendrick A.G., опубликованных в 1927. До сих пор она не утратила актуальности и часто применяется даже в современных исследованиях.
Данная модель хорошо подходит для моделирования эпидемий многих инфекционных заболеваний, включая ветрянку, корь, краснуху и многие другие. Вспышки подобных заболеваний обычно имеют циклическую природу, так как со временем число восприимчивых к заболеванию людей падает, и, до тех пор, пока класс восприимчивых не восполнится за счет новорожденных или приезжих, болезнь распространяться не может. В классической SIR-модели, рассматриваемой в данной работе, популяционная динамика не принимается во внимание. Мы предполагаем, что численность населения на протяжении всего рассматриваемого промежутка времени является постоянной.
Данной модели соответствует следующая система дифференциальных уравнений:

Данная модель, как нетрудно заметить,
зависит от двух параметров: параметр
 называется частотой контактов и, грубо
говоря, отвечает за возможность передачи
болезни при контакте между зараженным
и восприимчивым индивидами. Второй
параметр –
называется частотой контактов и, грубо
говоря, отвечает за возможность передачи
болезни при контакте между зараженным
и восприимчивым индивидами. Второй
параметр – – отвечает за переход объекта из класса
больных в класс выздоровевших. Иными
словами,
– отвечает за переход объекта из класса
больных в класс выздоровевших. Иными
словами,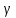 – это частота выздоровлений.
– это частота выздоровлений.
К сожалению, данная система нелинейна и не имеет общего аналитического решения. Впрочем, это не мешает при решении практических задач применять широко известные численные методы решения систем ОДУ. В данной работе используется метод Рунге-Кутта четвертого порядка точности.
Возможно, более наглядной является следующая диаграмма, иллюстрирующая переходы между состояниями:

Рис. 1 Диаграмма переходов между состояниями
Поскольку, как уже было сказано, модель довольно популярна, было разработано большое количество ее модификаций: SI-модель, которая успешно применяется для моделирования эпидемий заболеваний без продолжительного иммунитета (к примеру, простуда),SEIR-модель с дополнительной, «инкубационной» стадией заболевания (хорошо моделирует вспышки туберкулеза), модификации, принимающие во внимание колебания численности рассматриваемой группы людей, и многие другие. Помимо этого, производятся попытки использовать подобные подходы для моделирования других процессов. Довольно успешно модели типаSIRзарекомендовали себя в задачах моделирования эпидемий компьютерных вирусов.
