Московский государственный университет приборостроения и информатики

Кафедра КБ 5 Компьютерные системы автоматизации и управления

УТВЕРЖДАЮ

Заведующий кафедрой КБ5

_________ (Жуков Д.О.)

«___» _________ 2015 г.

Для студентов 4 курса института КБ

Специальности 220700

Доцент, к.т.н. Панайоти В.А.

ЛЕКЦИЯ № 4

по дисциплине «Диагностика и надежность автоматизированных систем» шифр 34304

ТЕМА: «Моделирование в диагностике»

Обсуждена на заседании кафедры

(предметно-методической секции)

«_ _» __________2015 г.

Протокол № _____

МГУПИ – 2015 г.

4. Моделирование в диагностике

Теоретически задача диагностики (в том числе индивидуальная) ставится следующим образом: на техническое состояние объекта влияют факторы, определяющие необратимые процессы деградации физико-химических свойств объекта, например, старение, износ и др. (см. вектор Х на Рис. 6). Влияют также случайные внешние и внутренние помехи (вектор Y).

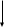
U

Sj

Х

x

СИ

Z

x*

СП

W e

Sj – экземпляр объекта

СИ – средство измерения

СП – средство прогнозирования

Рис. 6 Однолинейная схема системы прогнозирования

Для измерения выбрана совокупность {ξ_l, l = 1,2,…,n} параметров объекта (вектор x), относительно которых предполагается, что они существенно зависят от Х и позволяют при определенных средствах прогнозирования, реализующих алгоритм прогнозирования предсказать будущее техническое состояние объекта "е". Эти параметры называют прогнозирующими. В технической генетике решаются обратные задачи и данная модель как бы переворачивается.

На значения прогнозирующих параметров в общем случае накладываются помехи Y. При измерении параметров возможны погрешности измерения (вектор Z), вследствие чего вместо вектора x истинных значений, получается вектор x* ¹ x. На результаты прогнозирования, возможно, влияют погрешности собственно прогнозирования – вектор W. Таким образом, будущее техническое состояние объекта "е" зависит от нескольких случайных векторных аргументов:

е = f (Х, Y, Z, W). (1)

Зависимость (1) по существу и является моделью процесса прогнозирования.

Вероятностный характер этой модели определяется тем, что аргументы X, Y, Z и W являются существенно случайными функциями.

Получить зависимость (1) в явной аналитической форме для, сколько-нибудь сложных объектов практически невозможно. В связи с этим используют различные приемы упрощения как самой модели, так и процедур ее обработки. К этим приемам относится расчленение общей задачи прогнозирования на две самостоятельные задачи – задачу

измерения прогнозирующих параметров, когда работают с моделью вида:

x *_l = j_l (X, Y, Z), l = 1, 2, …, n (2)

и задачу получения прогноза (результата прогнозирования) по модели вида:

e = Y (x *, W). (3)

Однако и при таком расчленении трудности разработки практически эффективных методов прогнозирования для сложных объектов остаются значительными. Наиболее простой была бы явная аналитическая модель вида:

е = f_x (X), (4)

в которой отсутствует зависимость будущего состояния от случайных помех и погрешностей. Стремясь к "идеальной" модели (4), применяют различные способы математической обработки моделей вида (2) и (3) с целью уменьшения зависимости окончательных результатов измерения, прогнозирующих параметров и прогноза от случайных функций Y, Z, W. Эти способы заключаются главным образом в сглаживании случайных процессов применением операторов сглаживания, таких как, операторы математического ожидания, "текущего среднего" и других. Для применения операторов сглаживания необходимо знать характеристики сглаживаемых случайных процессов, например вероятности появления величин Y, Z и W, интервалов сглаживания и др., что сопряжено с необходимостью получения и обработки больших объемов априорной информации, что практически далеко не всегда возможно.

Аналитическое представление модели (3) затруднено даже в том случае, когда известны значения прогнозирующих параметров x* в прошлые периоды времени, т.е.: t_i Î Т₁, заданы диапазоны их допустимых значений и можно пренебречь погрешностями W. Задача выбора описания процесса изменения во времени рабочей точки, т.е. конца вектора x*, в области допустимых значений прогнозирующих параметров, а, следовательно, и выбора модели процесса эволюции технического состояния объекта прогнозирования остаётся всегда!

Задача достоверного и устойчивого измерения значений прогнозирующих (как и любых других) параметров, т.е. выбора и обработки модели (2), является типичной для теории и практики измерения. Специфическими для технического прогнозирования являются задачи построения и обработки модели (3) с целью получения прогноза, а также задачи выбора прогнозирующих параметров.

Для решения задачи выбора совокупностей прогнозирующих параметров не существует формализованных методов.

Даже для простых объектов прогнозирующие параметры выбираются интуитивно на основе знания функциональных, структурных, физико-химических и других свойств конкретных объектов с учетом условий эксплуатации и т.п.

При прогнозировании в конечном итоге нас интересует зависимость (4), где Х представляет факторы, определяющие необратимые изменения в объекте прогнозирования. Поэтому выбор и измерение прогнозирующих параметров в принципе не являются необходимыми. Однако, установить функциональную связь в явном виде между техническим состоянием "е" и фактором Х в общем случае не представляется возможным. Более того, измерение значений вектора Х часто весьма затруднено, если вообще возможно. Поэтому связь (4) устанавливают опосредованно через зависимость (2) путем измерения прогнозирующих параметров, относительно которых предполагается, что их значения изменяются во времени из-за воздействия факторов Х и затем через зависимость (3), экстраполируя значения прогнозирующих параметров на будущие периоды времени.

Таким образом, практическая реализация теоретически строгих постановок задач прогнозирования технического состояния объектов встречается с трудностями и ограничениями.

Априорные данные о технических характеристиках объекта можно получить от средств тестового и функционального диагностирования. Тем самым при достаточно "хороших" средствах функционального и тестового диагностирования и при условии организации накопления и обработки выдаваемой ими информации имеется возможность в любой период времени конкретного экземпляра объекта иметь не только абсолютные фактические значения интенсивностей отказов и прогнозирующих параметров, но также динамику их изменения, например в виде кривых. При наличии таких кривых можно эмпирически выбрать критерий годности и назначить его предельное значение, при достижении которого дальнейшее использование данного экземпляра объекта либо невозможно (опасно), либо не оправдано по технико-экономическим соображениям.

Удачный выбор критерия годности позволяет использовать его значения для управления периодичностью диагностирования (т.е. профилактики и ремонта) объекта. Это и является реализацией индивидуального прогнозирования технического состояния объекта и тем самым обслуживания его по состоянию.

Простейшими критериями годности могут быть: абсолютные значения или скорости изменения абсолютных значений интенсивностей отказов или некоторых (прогнозирующих) параметров

Конечно, наиболее трудными являются вопросы обоснованного назначения предельного значения критерия годности, а так же выбора прогнозирующих параметров. Теоретически обоснованные ответы на эти вопросы удаётся получить далеко не всегда и чаще только для очень простых объектов. В большинстве случаев, однако, могут оказаться приемлемыми методы экспертных оценок.