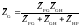2.2. Преобразование схем замещения

При расчетах токов короткого замыкания, как правило, возникает необходимость в преобразовании исходной схемы к более простому виду. Применение тех или иных методов преобразования зависит, прежде всего, от конфигурации исходной схемы, применяемого метода расчета, интересующих величин и от требований, предъявляемых к расчету.

Если исходная схема замещения не содержит замкнутых контуров, то она преобразуется в эквивалентную результирующую схему путем только последовательного и параллельного соединения элементов и путем замены нескольких источников, имеющих разные ЭДС и разные сопротивления, но присоединенных в одной точке, одним эквивалентным источником. При более сложных исходных схемах замещения для определения эквивалентного результирующего сопротивления можно использовать такие способы преобразования, как преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений; звезду сопротивлений в эквивалентный треугольник сопротивлений; многолучевую звезду сопротивлений в полный многоугольник сопротивлений и т.д. Формулы таких преобразований приведены в табл. 2.2.

Задачей расчета токов коротких замыканий обычно является нахождение тока в аварийной ветви или в месте короткого замыкания. Поэтому преобразование схемы удобнее вести так, чтобы аварийная ветвь, по возможности, была сохранена до конца преобразования. С этой целью концы нагрузочных ветвей, ЭДС которых принимаются равными нулю, не следует соединять с точкой короткого замыкания; лучше эти ветви объединить с генераторными в эквивалентные генерирующие ветви.

В случаях, когда исходная расчетная схема симметрична относительно точки короткого замыкания или какая-либо ее часть симметрична относительно некоторой промежуточной точки, то задачу определения эквивалентного результирующего сопротивления можно существенно упростить путем соединения на исходной расчетной схеме точек, имеющих одинаковые потенциалы, и исключения из схемы тех элементов, которые при коротком замыкании оказываются обесточенными.

Таблица 2.2

Основные формулы преобразования схем замещения

Вид преобразования	Исходная схема	Преобразованная схема	Сопротивление элементов преобразованной схемы
Последовательное соединение
Параллельное соединение			, где ; ; ; При двух ветвях
Замена нескольких источников эквивалентным			= При двух ветвях =
Преобразование треугольника в звезду
Преобразование трехлучевой звезды в треугольник
Преобразование многолучевой звезды в полный многоугольник			…………………, где Аналогично и при большем числе ветвей

Если в исходной схеме замещения один из лучей трехлучевой звезды сопротивлений содержит ЭДС, то часто бывает целесообразно звезду сопротивлений заменить на треугольник и затем последний разрезать по вершине, к которой приложена ЭДС, подключив при этом на каждом из оказавшихся свободными концов ветвей ту же ЭДС.

Если трехфазное КЗ находится в узле с несколькими сходящимися в нем ветвями, то этот узел можно расчленить, сохранив на конце каждой образовавшейся ветви такое же КЗ. Далее полученная схема преобразуется относительно любой из точек КЗ. При этом остальные ветви с КЗ учитываются как нагрузочные ветви с ЭДС, равными нулю. Этот прием особенно эффективен, когда необходимо найти ток в одной из ветвей, присоединенных к узлу с КЗ.

Иллюстрации применения рассмотренных преобразований представлены на рисунках 2.2 – 2.4.

Схема на рис.2.2, а принимает вид рис.2.2,б после замены треугольника сопротивлений эквивалентной звездой с лучами сопротивлений , определяемыми по выражениям:

На рис.2.1.3,а представлена схема, которая приводится к более простому виду после преобразования звезды с лучами в эквивалентный треугольник со сторонами и последующим размыканием полученного треугольника по узлу с ЭДС (рис. 2.3, б).

Рисунок 2.2 – Преобразование треугольника сопротивлений (2.2,а) в звезду (2.2,б).

Формулы преобразования звезды в эквивалентный треугольник:

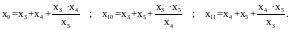
а) б)

Рисунок 2.3 – Преобразование трехлучевой звезды в эквивалентный треугольник (рис. 2.3,а) с последующим размыканием по узлу с ЭДС (рис. 2.3,б).

После параллельного сложения ветвей с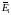 и ; и схема рис. 2.3,б приобретает вид схемы рис. 2.2 а, преобразование которой к более простому виду (рис. 2.2 б) рассмотрено выше.

При этом

Подобная замена возможна при любых значениях ЭДС. Пассивные ветви и ветви с точкой КЗ можно рассматривать как частные случаи, когда .

В качестве примера преобразования многолучевой звезды сопротивлений в полный многоугольник сопротивлений на рис. 2.4 представлено преобразование четырехлучевой звезды (рис. 2.4,а) в четырехугольник с диагоналями (рис. 2.4,б).

Рисунок 2.4 – Иллюстрация использования преобразования четырехлучевой звезды сопротивлений в четырехугольник с диагоналями.

Если четырехлучевую звезду с элементами 1,2,4,5, (рис.2.4,а) заменить четырехугольником 1n, 1f, n , f c диагоналями 1 и fn, то после размыкания по узлу с ЭДС и замены образовавшихся параллельных ветвей эквивалентными (x₆//x_nℓ; x₈//x_fℓ) схема (рис. 2.4,б) приобретает уже знакомый вид (рис.2.3,б).

Выбор кратчайшего пути преобразования достигается практикой решения подобных задач. Очевидные на первый взгляд преобразования не всегда являются наиболее рациональными, так как могут в дальнейшем привести к усложнению схемы и, следовательно, к увеличению вычислительной работы. Поэтому прежде, чем производить вычислительные операции, следует наметить ход предполагаемых преобразований.
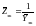