Питання до захисту :
Чи може задача цілочисельного програмування мати кілько розв’язань?
Відповідь:________________________________________
_________________________________________________
Які е методи розв’язання цілочисельних задач?
Відповідь:________________________________________
_________________________________________________
Чи може цільова функція виявитися необмеженою?
Відповідь:________________________________________
_________________________________________________
Чи може оптимальне значення цільової функції цілочисельної лінійної програми виявитися нецілочисельної?
Відповідь:________________________________________
_________________________________________________
Роботу виконав Роботу перевірив
Практична робота №7 «Розв’язання задач дрібно-лінійного програмування»
1 Тема роботи: Дрібно-лінійне програмування.
2 Мета роботи: Вивчити методи розв’язання задач дрібно-лінійного програмування.
3 Теоретичний матеріал
Розглянемо завдання в загальній постановці: знайти екстремум (max або min) дробово-лінійної цільової функції:
→ extremum
(1)
області G, що визначається канонічною системою лінійних обмежень
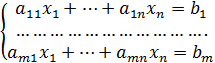(2)
c умовою
неотрицательности: 
. (3)
Без обмеження
спільності можна вважати, що знаменник
функції (1) в області G в нуль не звертається
і зберігає знак
так, що в подальшому вважаємо: 
(4)
Співвідношення (1)-(4) - визначають завдання ДЛП.
Введемо нові змінні:
у0
= ( 
)-1
; yj=
y0xj,
j=
(5)
підставимо (5) в (1) - (4). В результаті отримаємо:
→ extremum
(6)
(7)
(8)
Крім того, з співвідношень (5) виходить ще один рівняння:
:
(9)
Таким чином, від завдання ДЛП виду (1) - (4) за допомогою перетворень (5) ми прийшли до задачі (6) - (9), в якій цільова функція (6) і система обмежень (7) - (9) лінійні, тобто отримали завдання ЛП виду (6) - (9), еквівалентну вихідної нелінійної задачі ДЛП виду (1) - (4).
Відзначимо, що перехід (5) від нелінійної задачі ДЛП (1) - (4), з n параметрами управління х1...хn, призводить до еквівалентної задачі ЛП (6) - (9), що містить n+1 параметрів управління у0, у1...уn, тобто лінеаризація завдання ДЛП досягається за рахунок збільшення її розмірності на 1.
4.Постановка завдання:
Вихідні дані обираються за варіантами:
1.
2.
x1 + 2x2 ≤ 16, –x1 + x 2 + 3x3 = 8,
x1 + x2 ≤ 10, 2x1 – x2 – x3 = 4,
x1 ≤ 6, xj ≥ 0, j = 1, 2, 3.
x2 ≤ 7,
x1, x2 ≥ 0
3.
4.
x1 – x2 + 2x3 = 4, x1 + x 2 + x5 = 3,
–x1 + 2x2 + x3 + x4 = 6, 3x1 + x2 – x3 = 4,
xj ≥ 0, j = 1,..4. –x1 + 3x2 + x4 = 6,
xj ≥ 0, j = 1,..5.
5.
6x1 – 3x 2 + x3 + x4 = 12, x1 + x 2 + x3 = 6,
7x1 – x2 + 2x3 ≤ 12, 3x1 – 2x2 + x4 = 9,
–4x1 + 2x2 – x3 – x5 = 1, –x1 + 2x2 + x5 = 10,
xj ≥ 0, j = 1,..5. xj ≥ 0, j = 1,..5.
7.
4x1 – x 2 ≤ 5, –x1 + 3x 2 – x4 = 10,
x1 + 3x2 – x3 = 7, 2x1 + 4x2 – x3 – x4 = 20,
–3x1 + 4x2 + x4 = 17, 5x1 + 2x2 + x5 = 35,
xj ≥ 0, j = 1,..4. –3x1 + 2x2 + x6 = 11,
xj ≥ 0, j = 1,.6.
9.
x1 + x 2 – x3 = 5,
–x1 + 2x2 ≥ 1,