Питання до захисту :
Якими методами будується опорний план?
Відповідь:________________________________________
_________________________________________________
За якими ознаками перевіряється перетворення
опорного плану на оптимальний?
Відповідь:________________________________________
_________________________________________________
Як визначається тип транспортної задачі?
Відповідь:________________________________________
_________________________________________________
Роботу виконав Роботу перевірив
Практична робота №5 «Розв’язання задач лінійного програмування параметричним методом»
1 Тема роботи: Параметричне програмування.
2 Мета роботи: Вивчити методи розв’язання задач параметричного програмування.
3 Теоретичний матеріал
Алгоритм для вирішення задач параметричного лінійного програмування в разі залежності від параметра коефіцієнтів цільової функції незначно відрізняється від звичайного симплексного методу.
Процес знаходження рішення задачі включає наступні етапи:
Вважаючи значення параметра λ рівним деякому числу
,
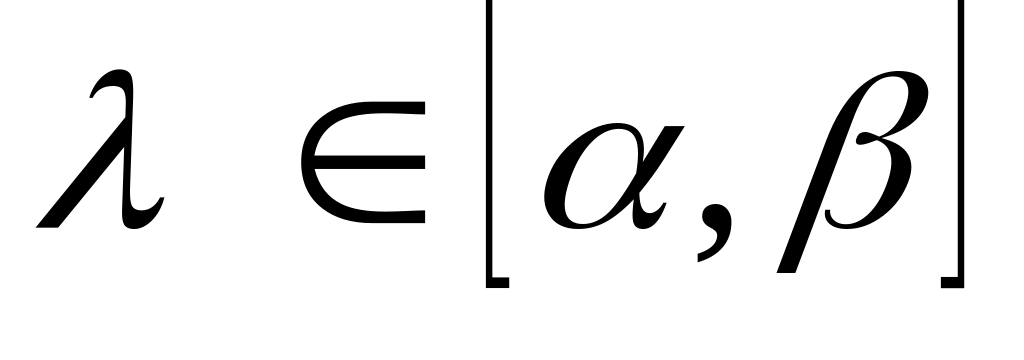знаходимо
оптимальний
план
або
встановлюємо
нерозв'язність
отриманої
завдання
лінійного
програмування.Визначають безліч значень параметра λ, для яких знайдений оптимальний план є оптимальним або завдання нерозв'язна. Ці значення параметра виключаються з розгляду.
Вважають значення параметра λ рівним деякому числу, що належав решти проміжку [α, β], і знаходять рішення отриманої завдання лінійного програмування.
Визначають множина значень параметра λ, для яких новий оптимальний план залишається оптимальним або завдання нерозв'язна. Обчислення повторюються до тих пір, поки не будуть досліджені всі значення параметра .
4. Постановка завдання:
Вихідні дані обираються за варіантами:
1. Максимізувати функцію
L ( x , λ ) = ( 1 - λ ) x 1 – ( 2 + 3 λ ) x 2 + x 3
при обмеженнях
x 1 + 4 x 2 + x 3 = 5
x 1 - 2 x 2 + x 3 = – 1
x 1, x 2, x 3 ≥ 0
– ∞ < λ< + ∞
. 2. Максимізувати функцію
L ( x , λ ) = x 1 – ( 5 + λ ) x 2 – ( 1 + λ ) x 3 + x 4
при обмеженнях
x 1 + 3 x 2 + 3 x 3 + x 4 = 3
2 x 1 + 3 x 3 – x 4 = 4
x 1, x 2 , x 3, x 4 ≥ 0
– ∞ < λ< + ∞
3. Максимізувати функцію
L ( x , λ ) = ( 1 - λ ) x 1 + ( 1 + λ ) x 2 – x 3
при обмеженнях
x 1 – x 2 – x 3 = 4
x 1 + 1 5 x 2 + x 3 = 2
x 1, x 2 , x 3 ≥ 0
– ∞ < λ< + ∞
4. Мінімізувати функцію
L ( x , λ ) = – x 1 – ( 4 – λ ) x 2 – ( 1 + 2 λ ) x 3
при обмеженнях
4 x 1 + 1 1 x 2 + 3 x 3 = 7
x 1 + x 2 – x 3 = 0
x 1, x 2 , x 3 ≥ 0
– ∞ < λ< + ∞
5. Максимізувати функцію
L ( x , λ ) = ( 1 – λ ) x 1 + ( 3 – λ ) x 2 + 5 x 3
при обмеженнях
x 1 + 2 x 2 – x 3 = 2
x 1 – x 2
= 6
x 1, x 2 , x 3 ≥ 0
– ∞ < λ< + ∞
6. Мінімізувати функцію
L ( x , λ ) = (λ - 1 ) x 1 – ( 4 + λ ) x 2 – ( 1 + 5 λ ) x 3
при обмеженнях
x 1 – x 2 + x 3 = 3
2 x 1 – 5 x 2 – x 3 = 0
x 1, x 2, x 3 ≥ 0
– ∞ < λ< + ∞
7. Максимізувати функцію
L ( x , λ ) = x 1 + ( 2 – 1 0 λ ) x 2 – ( 1 + λ ) x 3
п р и у с л о в и я х
x 1 + 7 x 2 + 9 x 3 = 8
x 1 + 3 x 2 + 5 x 3 = 4
x 1, x 2 , x 3 ≥0
– ∞ < λ< + ∞
8. Максимізувати функцію
L ( x , λ ) = ( 1 - λ ) x 1 + ( 8 - 2 λ ) x 2 ++ ( 1 0 + λ ) x 3
при обмеженнях
x 1+ x 2 + 4 x 3 = 2
x 1 – x 2 + 2 x 3 = 0
x 1, x 2, x 3 ≥ 0
– ∞ < λ < + ∞