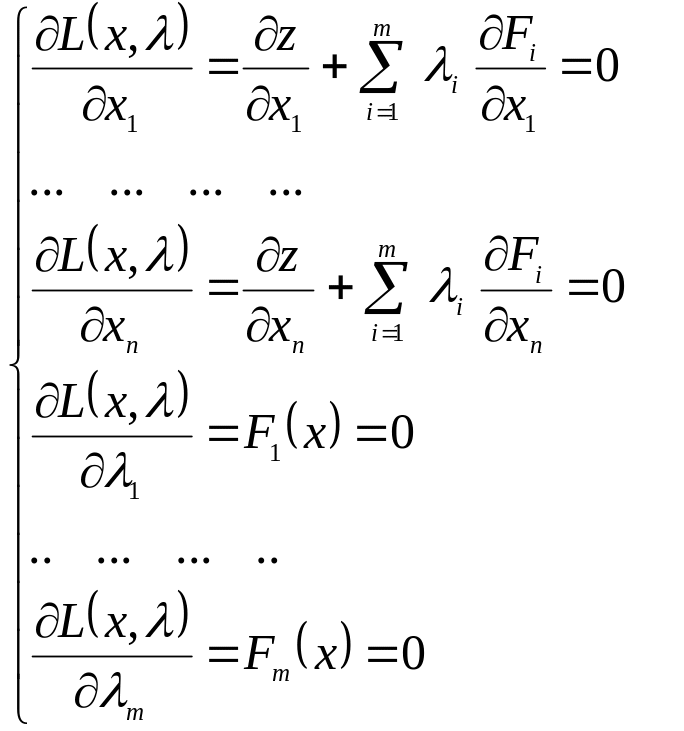3 Теоретичний матеріал
Розглянемо загальну задачу НЛП
|
(1) |
|
(2) |
в якій функції
два рази неперервно диференційовні.
Для визначення її оптимальних точок
користуються функцією Лагранжа
|
(3) |
яка дозволяє задачу з обмеженнями звести до задачі без обмежень. Цілком очевидно, що на обмеженнях (6)
і
.
Необхідні умови
оптимальності точки
функції
мають вигляд:
|
(4) |
або в розгорнутій формі
|
(5) |
З системи
рівнянь
(5) видно,
що для її побудови достатньо взяти
частинні похідні по
x
від функції Лагранжа, прирівняти їх до
нуля і додати до них систему обмежень
(2).
Характер оптимальності
точки визначаємо за допомогою достатніх
умов.
Причому
застосовуємо їх лише до функції
,
оскільки
4.Постановка завдання:
Вихідні дані обираються за варіантами:
1. Мінімізувати функцію
за умови
2. Знайти умовний екстремум функції
z(x,y)=x+3y
за умови x 2 +y 2 =10. .
3.Знайти умовний екстремум функції
за умови
4. Знайти умовний екстремум функції
z(x,y)=x2-4y
за умови x - y =1
5. Знайти умовний екстремум функції
z(x,y)=2x+4y
за умови x 2 +4y 2 =8..
6. Знайти умовний екстремум функції
z(x,y)=x+2y
за умови x 2 +y 2 =5.
7. Знайти умовний екстремум функції
z(x,y)=6 - 4x - 3y
за умови x 2 +y 2 =1.
8. Знайти умовний екстремум функції
z(x,y)=4x + x 2 + 8y +y 2
за умови x +y =200.
9. Знайти умовний екстремум функції
z(x,y)=2 x 2 + xy +y 2
за умови 2x +3y =5.
10. Знайти умовний екстремум функції
z(x1,x2,x3)= x1 – 2x2 + 2x3
за умови x12+ x22 + x32 =5.
11. Знайти умовний екстремум функції
z(x1,x2)= x1 x2
за умови x12+ x22 =2.
12. Знайти умовний екстремум функції
z(x,y)=xy
за умови 2x +3y =1.
Питання до захисту :
Якою літерою позначено множник Лагранжу?
Відповідь:________________________________________
_________________________________________________
Чи може множник Лагранжа приймати від’ємне значення?
Відповідь:________________________________________
_________________________________________________
В яких випадках екстремуму не існує?
Відповідь:________________________________________
_________________________________________________
Які умови перетворення умовний екстремуму в безумовний екстремум ?
Відповідь:________________________________________
_________________________________________________
Роботу виконав Роботу перевірив
Додаток А
Зразок титульного листа
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКИЙ КОМПЮТЕРНО-ТЕХНОЛОГІЧНИЙ
КОЛЕДЖ НТУ «ХПІ»
ЖУРНАЛ
ЗВІТІВ ПРО ВИКОНАННЯ
ПРАКТИЧНИХ РОБІТ
з дисципліни
«Математичні методи дослідження операцій»
Студента Перевірив
_________________ викладач
Шварц О.А.
Харків 2016
Додаток Б
Зразок титульного листа
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКИЙ КОМПЮТЕРНО-ТЕХНОЛОГІЧНИЙ
КОЛЕДЖ НТУ «ХПІ»
ЗВІТ
ПРО ВИКОНАННЯ
ПРАКТИЧНОЇ РОБОТИ №____
з дисципліни
«Математичні методи дослідження операцій»
Варіант №__
Студента Перевірив
_________________ викладач
Шварц О.А.
Харків 2016