- •Практична робота №1 «Графічний метод розв’язання злп»
- •3 Теоретичний матеріал
- •4 Постановка завдання:
- •Питання до захисту :
- •Практична робота №2 «Розв’язання задач лінійного програмування симплекс-методом »
- •3 Теоретичний матеріал.
- •Алгоритм симплекс-методу
- •4 Постановка завдання:
- •Питання до захисту :
- •Практична робота №3 «Розв’язання задач лінійного програмування двійковим симплекс-методом»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
- •Практична робота №4 «Розв’язання транспортних задач методом потенціалів»
- •3 Теоретичний матеріал
- •4 Постановка завдання:
- •Питання до захисту :
- •Практична робота №5 «Розв’язання задач лінійного програмування параметричним методом»
- •3 Теоретичний матеріал
- •4. Постановка завдання:
- •Питання до захисту :
- •Практична робота №6 «Розв’язання задач цілочисельного програмування»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
- •Практична робота №7 «Розв’язання задач дрібно-лінійного програмування»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
- •Практична робота №8 «Графічний метод розв’язання задач нелінійного програмування»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
- •Практична робота №9 «Знаходження екстремуму функції двох змінних»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
- •Практична робота №10 «Розв’язання задач нелінійного програмування методом множників Лагранжа»
- •3 Теоретичний матеріал
- •4.Постановка завдання:
- •Питання до захисту :
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКИЙ КОМП’ЮТЕРНО-ТЕХНОЛОГІЧНИЙ КОЛЕДЖ НТУ «ХПІ»

Методичні рекомендації
щодо виконання практичних робіт
з дисципліни
«Математичні методи дослідження
операцій»
Харків 2016
Методичні рекомендації щодо виконання лабораторних робіт з дисципліни «Математичні методи дослідження операцій» для студентів ХКТК НТУ «ХПІ» спеціальності: 5.05010101 “Обслуговування програмних систем і комплексів” та 5.05010301 “Розробка програмного забезпечення”.
Розроблена викладачем Шварц О.А.
Розглянута і затверджена на засіданні циклової комісії компютерних та інформаційних дисциплін
Протокол № 1 від « 1 » вересня 2015 р.
Голова комісії _________________ О.І. Ігнатенко
Заступник директора
з навчальної роботи _______________ О.І. Ігнатенко
Практична робота №1 «Графічний метод розв’язання злп»
1 Тема роботи: Графічний метод розв’язання ЗЛП.
2 Мета роботи: Вивчити графічний метод розв’язання ЗЛП на найпростіших прикладах.
3 Теоретичний матеріал
Графічний метод доцільно застосовувати для розв'язування задач лінійного програмування із двома змінними. Обмежене використання даного методу зумовлене складністю побудови багатокутника розв'язків для задач з трьома змінними, а графічне зображення де кількість змінних перевищує число три, взагалі неможливе.
Розглянемо задачу лінійного програмування:
![]() при
обмеженнях:
при
обмеженнях:
![]()
![]()
Згідно даному
методу, кожна нерівність системи (2)
визначає півплощину з граничною прямою![]() і серед всіх цих півплощин можна вибрати
спільну частину, або переріз усіх
зазначених півплощин, тобто множину
точок, координати яких задовільняють
усі обмеження задачі — багатокутник
розв'язків.
і серед всіх цих півплощин можна вибрати
спільну частину, або переріз усіх
зазначених півплощин, тобто множину
точок, координати яких задовільняють
усі обмеження задачі — багатокутник
розв'язків.
Звідси випливає, що розв'язати задачу лінійного програмування графічним методом, означає знайти таку вершину багатокутника розв'язків, у результаті підстановки координат якої в (1) функція мети набуває свого максимального або мінімального значення.
Алгоритм графічного методу складається з таких етапів:
Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях (2) знаків нерівностей на знаки рівностей.
Визначаємо півплощини, що відповідають кожному обмеженню задачі.
Знаходимо багатокутник розв'язків задачі лінійного програмування.
Будуємо вектор
 ,
який задає напрямок зростання значення
цільової функції.
,
який задає напрямок зростання значення
цільової функції.Будуємо пряму
 ,
перпендикулярну до вектора
,
перпендикулярну до вектора
 .
.Рухаючи пряму в напрямку вектора ( для задачі на знаходження максимуму ) або в протилежному напрямку ( для задачі на знаходження мінімуму ), знаходимо вершину багатокутника розв'язків, де цільова функція набуває свого екстремального значення.
Визначаємо координати точки, в якій функція мети набирає свого максимального чи мінімального значення і обчислюємо значення даної функції в цій точці.
При використанні графічного методу для знаходження розв'язку задачі лінійного програмування можливі такі випадки:
1. Функція мети є необмеженою на множині розв'язків. В такому випадку задача лінійного програмування не має оптимальних планів.

2. Система обмежень є несумісною. Функція мети оптимальних планів не має також.

4. Цільова функція набуває максимального значення в єжиній точці A багатокутника розв'язків.

4. Цільова функція набуває максимального значення в будь-якій точці відрізка AB.

4 Постановка завдання:
Вихідні дані обираються за варіантами
Мінімізувати функцію
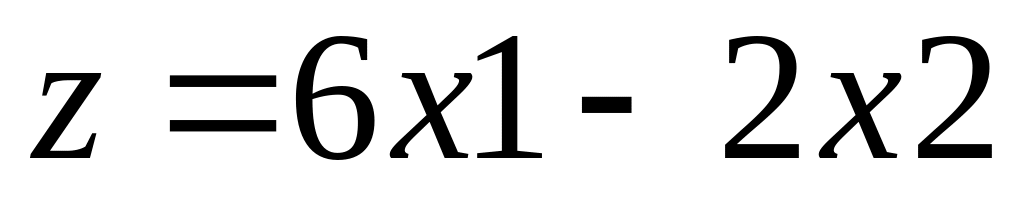
при обмеженнях
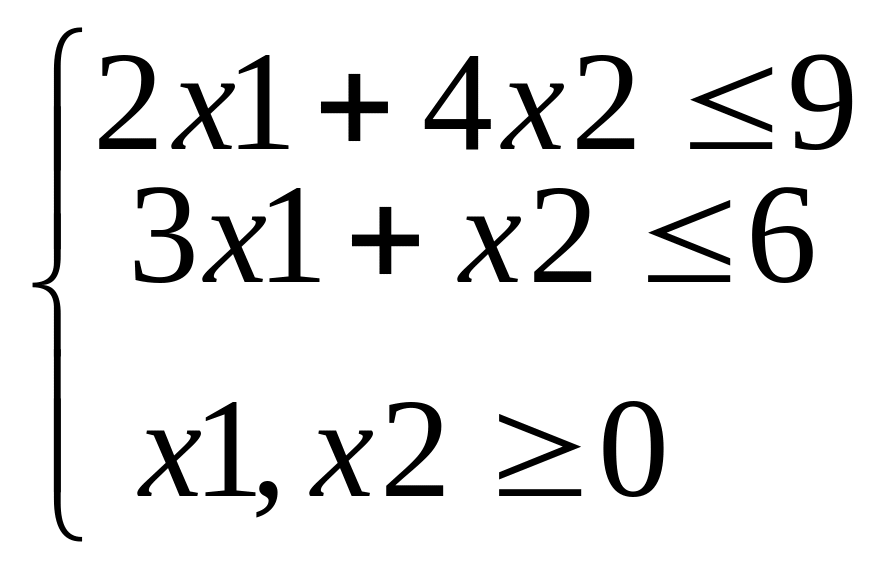
Мінімізувати функцію
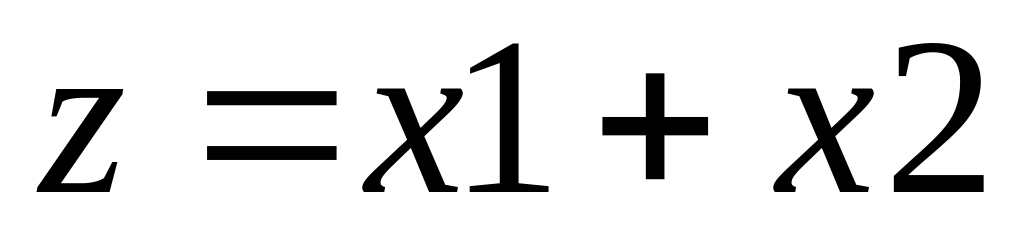
при обмеженнях
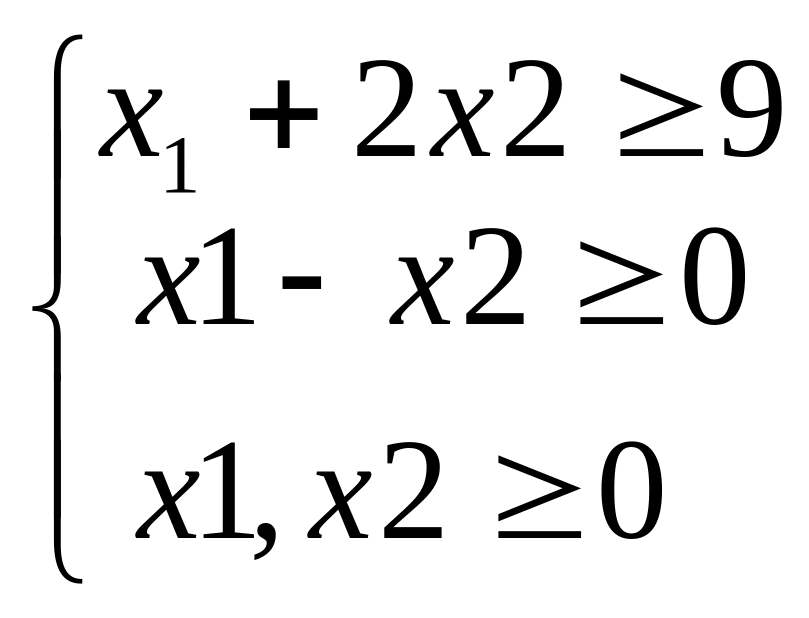
Мінімізувати функцію

при обмеженнях
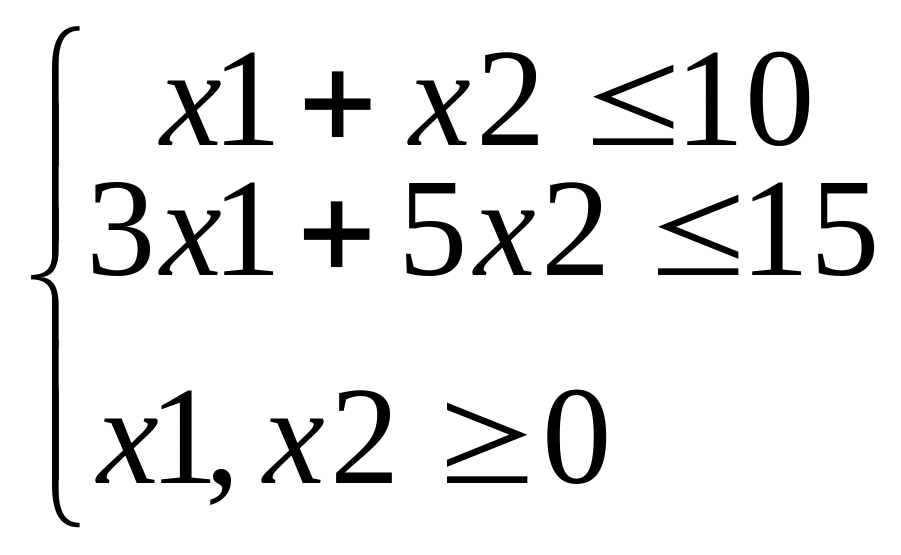
f(x) = 2x1+3x2 max,
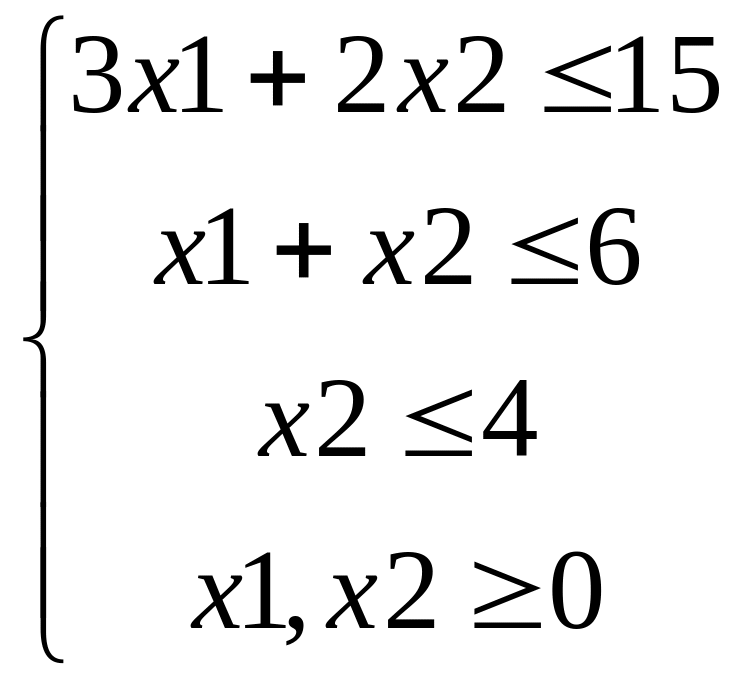 .
.
.f(x)=2x1−3x2 min,
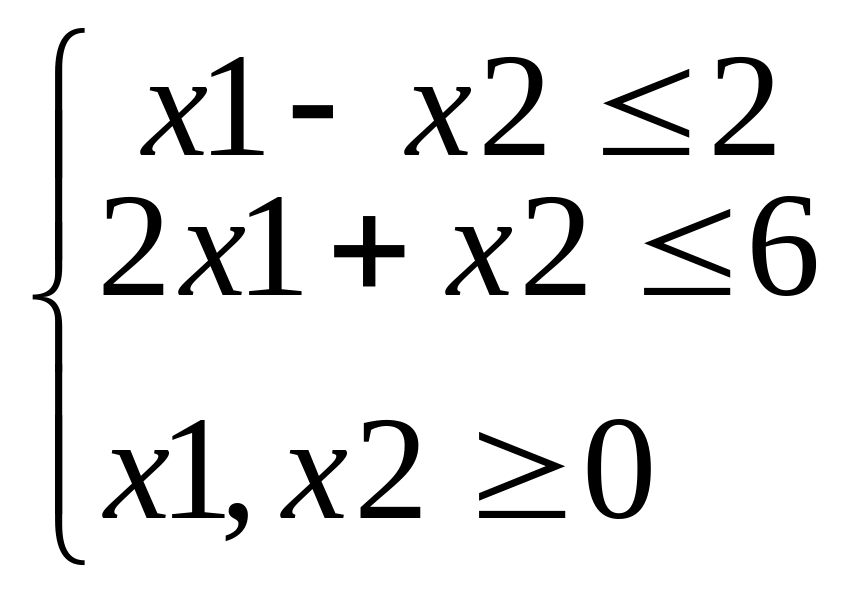
f(x) = −3x1+4x2 min,
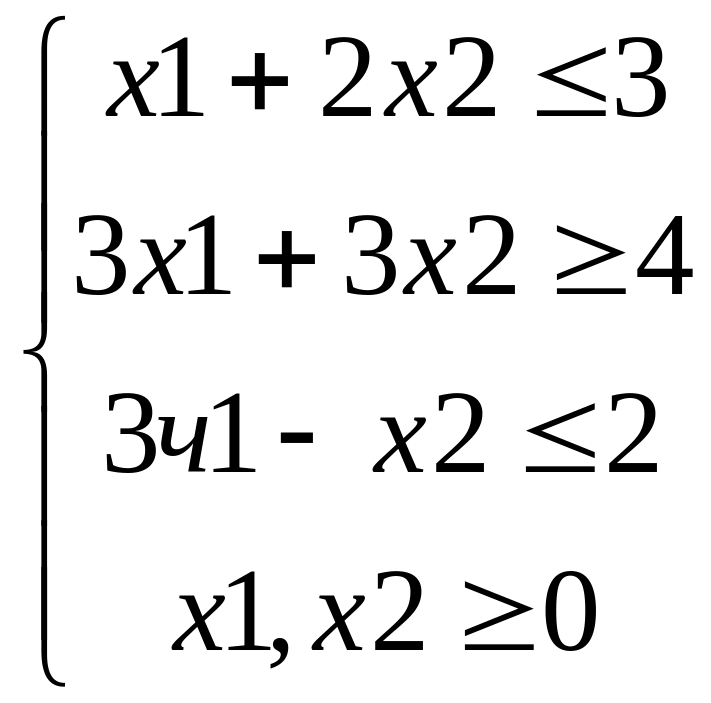
7.
Мінімізувати функцію
![]()
при обмеженнях
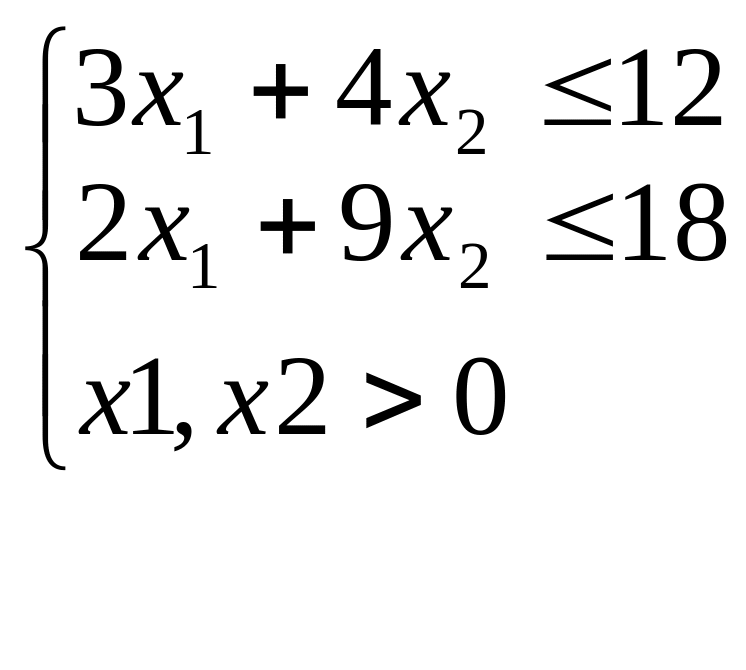
Максимізувати функцію
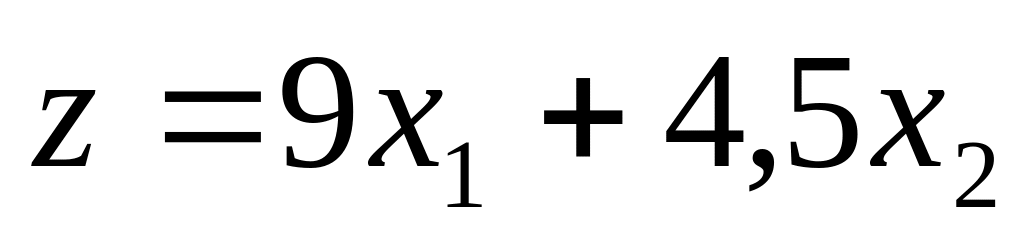
при обмеженнях
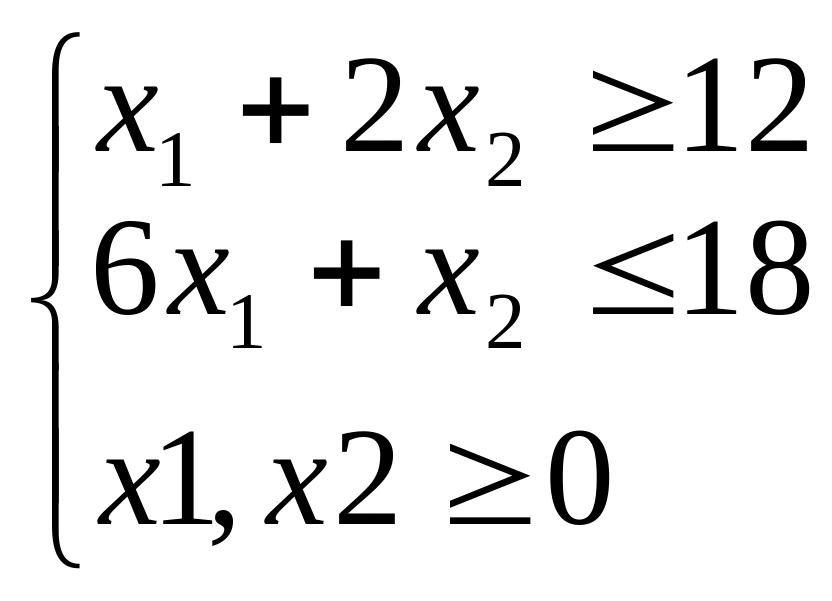
Мінімізувати функцію
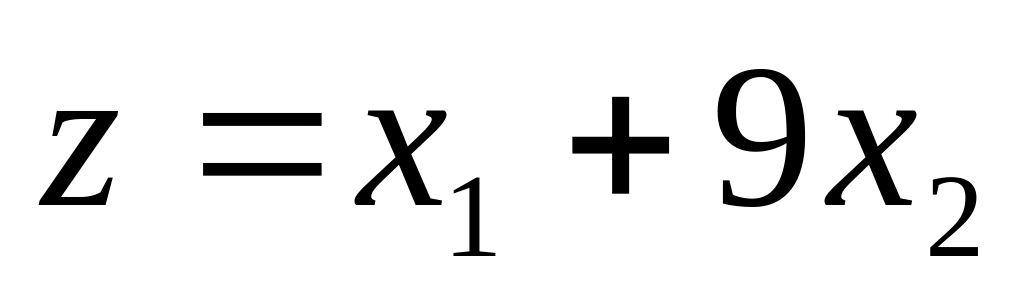
при обмеженнях
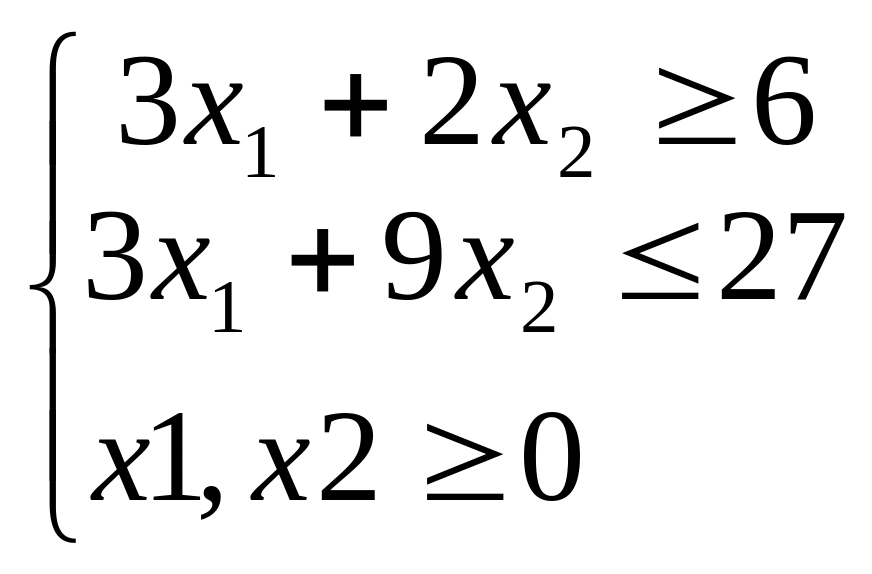
Максимізувати функцію
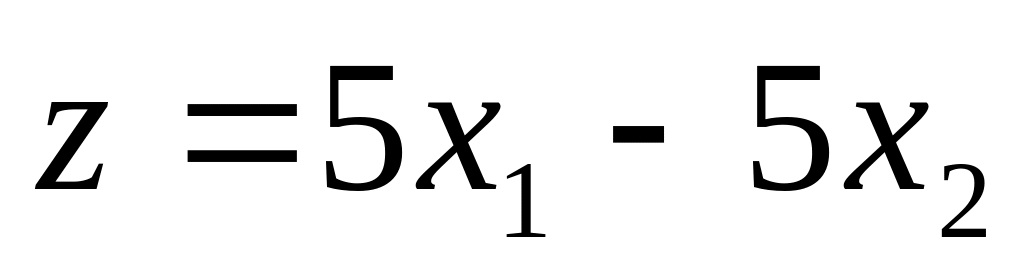
при обмеженнях