5 Хід виконання практичної роботи

Завдання математичного програмування вирішуються за допомогою вбудованих функцій

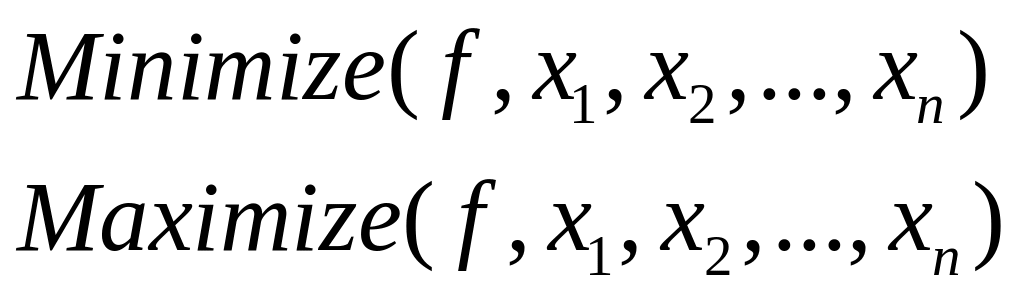
1. Запустимо програму, перед нами з'явиться робоче вікно зі всіма вбудованими функціями. Всі вони прості у вживанні і представлені на панелі інструментів:

2. Занесемо первинні дані: нашу цільову функцію, яка залежить від змінних і значення самих змінних:

2. Для того, щоб внести до програми існуючі обмеження нам знадобиться функція:

4. Тепер залишається лише задати функцію і запустити програму:

Рішення задачі перед нами.

Питання до захисту :

В якому вигляді виводяться змінні даної задачи?

Відповідь:________________________________________

_________________________________________________

Чі можливо використовувати функції Min, Max для розв’язання даної задачи?

Відповідь:________________________________________

_________________________________________________

Якій роздільник використовується між дрібною та цілою частиною в пакеті Mathcad?

Відповідь:________________________________________

_________________________________________________

Що таке оптимальне рішення задач лінійного програмування?

Відповідь:________________________________________

_________________________________________________

Роботу виконав Роботу перевірив

Лабораторна робота №3 «Розв’язання задач цілочисельного програмування в пакеті Mathcad»

1 Тема роботи: Цілочисельне програмування.

2 Мета роботи: Вивчити методи розв’язання задач цілочисельного програмування в пакеті Mathcad.

3 Теоретичний матеріал

Значна частина економічних завдань, в тому числі й в галузі стратегічного менеджменту, потребує за своїм змістом цілочисельного рішення, коли змінні величини визначають кількість неподільних одиниць продукції, устаткування, заготовок тощо. В багатьох випадках такі завдання вирішуються звичайними методами, наприклад, симплексним, з наступним приведенням до цілих чисел. Але такий підхід виправданий, коли одиниця невимірно мала порівняно з усім обсягом (наприклад, товарних запасів); в іншому випадку цей підхід може суттєво спотворити дійсно оптимальне рішення.

Метод Гоморі для лінійних завдань цілочисельного програмування заснований на понятті конгруентності дійсних чисел. Будь-яке дійсне число можна представити у вигляді суми його цілої та дробової частини: х=[х]+{х}, де квадратні дужки означають цілу частину, а фігурні - дробову. Наприклад, 7,5 = [7,5]+{7,5}=7+0,5.Якщо позначити конгруентність чисел символом є, то, наприклад, 7,5 є 0,5; 6,3 є 0,3.

За методом Гоморі розв'язок цілочисельних задач на першому етапі нічим не відрізняється від простого розрахунку за симплексним алгоритмом. Якщо серед значень змінних в оптимальному плані є дроби, то складається додаткове обмеження, що відсікає частину рішення, але залишаються всі інші умови, які повинен задовольняти оптимальний план. Це додаткове обмеження приєднується до вихідних обмежень задачі, та знову застосовується процедура симплексного методу. Алгоритм Гоморі дозволяє прийти до оптимального цілочисельного рішення за кінцеву кількість кроків.