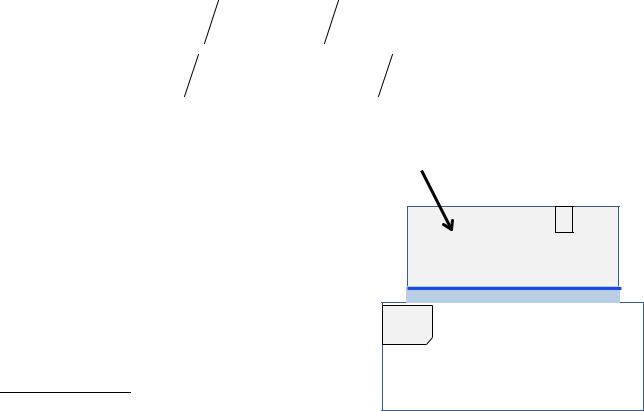
Point of Zero Charge
|
|
|
|
|
H |
+ |
|
Ka |
− Kb |
H |
+ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Q = 0 = qN0 |
|
|
|
|
|
|
|
S |
|
|
|
|
|
S |
|
|
|
|
1 |
+ K |
|
H+ |
|
+ H+ |
|
K |
|
|
|||||||||
|
|
|
b |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
S |
|
S |
|
|
a |
|
||
|
+ 2 |
= |
|
|
|
+ 2 |
|
|
|
|
|
pH |
|
|||||
Ka Kb = H |
|
S |
H |
B |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ka =10− pKa , Kb =10− pKb
ID
pzc = pKa + pKb
2
pKa = −2, pKb = 6
For SiO2
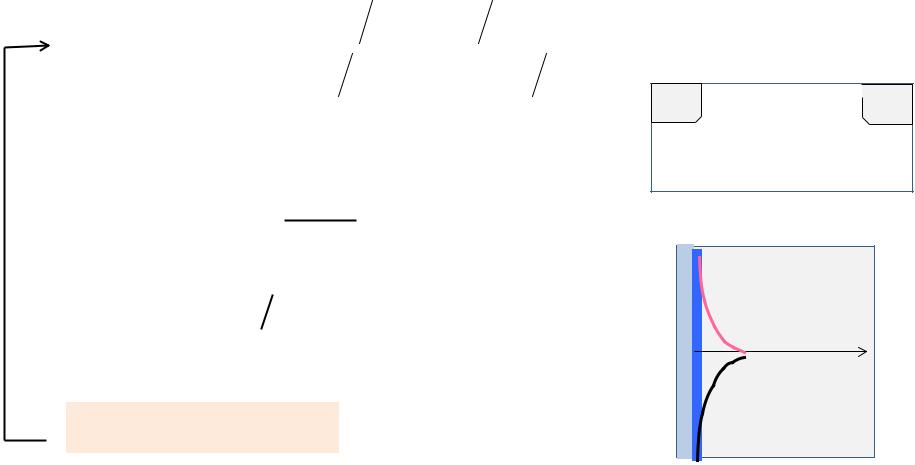
Self-consistent surface charge
|
|
|
H |
+ |
|
Ka |
− Kb |
H |
+ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Q( pH ) = qN0 |
|
|
|
|
|
S |
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
+ K |
b |
|
H+ |
|
+ H+ |
|
K |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
S |
|
S |
|
|
a |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Q =QDL +QMOS
~QDL =Q0 exp zqψ0
kBTL
ψ |
0 |
= kBTL ln Q Q |
pH |
|
|
zq |
0 |
|
|
|
|
|
|
|
[H+ ]S =[H+ ]Be−qψ0 /kBT
|
|
|
|
|
δQ |
≡ −qβint |
Intrinsic buffer capacity |
|
δ (pHs ) |
||
|
|
|
Aside: Surface potential and Buffer capacity
[H+ ]S =[H+ ]Be−qψ0 /kBT
pH
pHs = pHB + qψ0 
2.3kBT
|
δψ0 |
= |
|
|
|
δψ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
δ pHs |
|
|
δ (pHB )+δ (qψ0 |
2.3kBT ) |
|
|
|
|
|
|
|
|
|||||||||
|
δψ0 |
= |
δψ0 |
× |
|
δQ |
|
= |
1 |
×(−qβint ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
δ (pHs ) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
δ pHs |
|
|
δQ |
|
|
CDL |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
δψ0 |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= −2.3 kT |
1+ |
2.3kBTCDL |
|
|
|
|
|
|
|
|
|
|||||||||
|
δ pHB |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
q |
|
q2 βint |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12
Outline
1)How to calculate pH
2)pH and surface charge
–Surface binding model
3)Nernst Limit of an ISFET
4)Conclusions
Alam, Principles of Nanobiosensors, 2013 |
13 |
|