Principles of Electronic Nanobiosensors
Unit 2: Settling Time
Lecture 2.2: Classical Sensors I
By Muhammad A. Alam
Professor of Electrical and Computer Engineering Purdue University
alam@purdue.edu
1
Outline
•Introduction
•So many sensors ... How to classify them
•Geometry of diffusion defines response time
–Approach based on ‘diffusion triangle’
–Approach based on ‘diffusion capacitance’
•Conclusion
|
Alam, Principles of Nanobiosensors, 2013 |
2 |
|
Nanobiosensors are highly sensitive
aM |
fM |
|
|
pM |
|
|
|
|
|
|
|
|
nM |
µM |
|
|
|
|
|
|
|
|
mM |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Is there something fundamental about the geometry?
Alam, Principles of Nanobiosensors, 2013 |
3 |
|
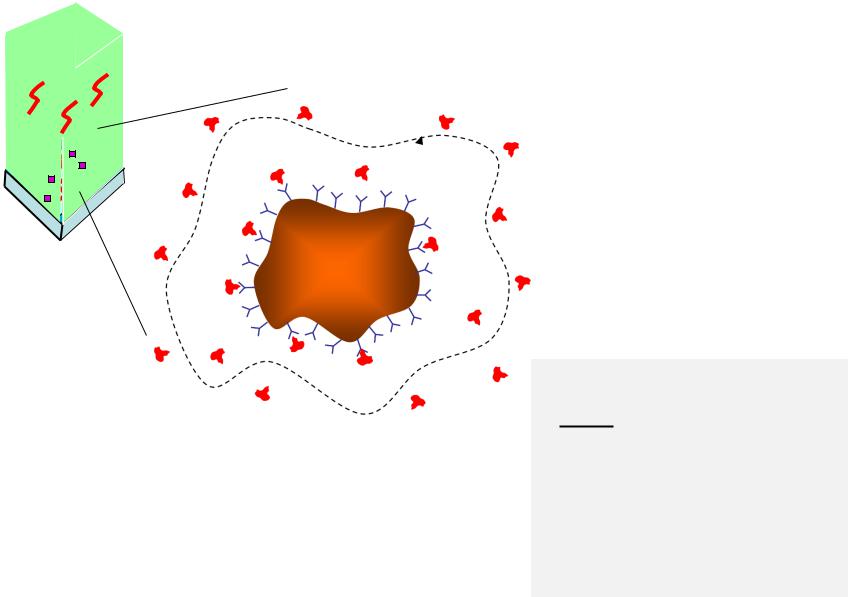
Settling time for biosensors
W
ddtρ = D 2 ρ
The diffusion-capture problem |
dN |
= kF (N0 − N)ρs |
is very challenging, especially for |
||
complex capture surfaces |
dt |
|
|
|
Alam, Principles of Nanobiosensors, 2013 |
4 |