Exact solutions in 3D
d ρ = 2 ρ |
|
|
Dρ |
|
|
a |
|
|
|
|
|
|||||
dt |
D |
|
J (t) = |
|
0 |
1 |
+ |
|
0 |
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
6Dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dN |
= kF (N0 − N)ρs |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
dt |
|
N(t) = 4πa02 ∫0 |
J (t ')dt ' |
|
|
|
|
|
||||||||
|
|
N(t) = 4πρ0 Da0 t +(a0 |
|
) |
|
|
||||||||||
kF →∞, ρs = 0 |
|
6D |
t |
|||||||||||||
|
|
|
N(t) ~ 4πρ |
Da t1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Alam, Principles of Nanobiosensors, 2013 |
9 |
Summary: For integer sensors
|
3−D |
|
|
|
F |
|
(1 ≤ DF ≤ 2) |
N (t) ρ0ts |
2 |
|
DF = 2 |
DF = 1 |
|
N (t) ρ0t1s |
(0 ≤ DF ≤1) |
DF = 0
Alam, Principles of Nanobiosensors, 2013 |
10 |
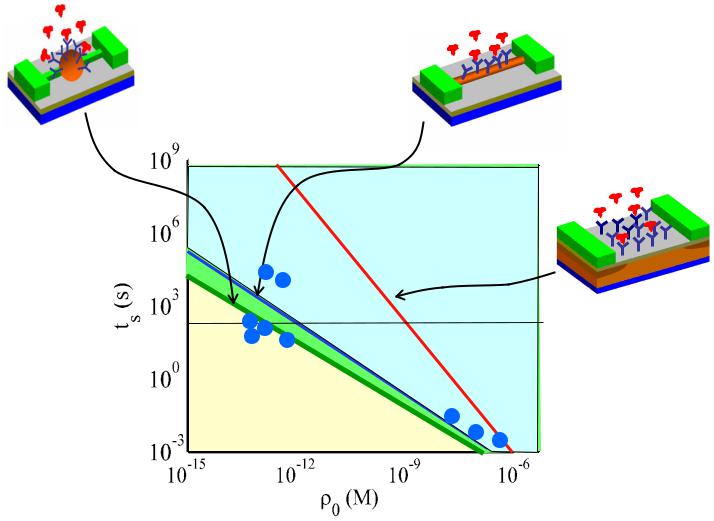
Performance limit of biosensors
Nanodot |
Nanowire |
|
|
|
100s |
Planar
Hahm et al., 2004, Zheng et al., 2005, Li et al., 2005, Kuznesow et al., 2006,
Gao et al., 2007, Stern et al., 2007
Nanodots sensor offer no significant additional advantage!
11
Conclusions
•Settling time defines the average time needed for a sensor to capture the minimum number of molecules required for definitive response.
•This time defines a fundamental limit to detection limit – almost analogous to the Heisenberg uncertainly principle.
•Size of the biomolecule is hidden in diffusion coefficient.
•Geometry of diffusion determines the response time.
Alam, Principles of Nanobiosensors, 2013 |
12 |