Principles of Electronic Nanobiosensors
Unit 2: Settling Time
Lecture 2.5: Beating the Limits – Barcode Sensors
By Muhammad A. Alam
Professor of Electrical and Computer Engineering Purdue University
alam@purdue.edu
1
A ‘fundamental’ relationship of biosensor
D=1 |
1<D<2 |
D=2 |
|
|
3−D |
|
− |
F |
|
|
ρ0 = Ns ×ts |
|
2 |
|
… not as fundamental as the uncertainty principle!
Alam, Principles of Nanobiosensors, 2013 |
2 |
Outline
•Three approaches to beat the diffusion limit
•Technique of distributed sensors: Biobarcode
•Physics of biobarcode operation
•Enhancement of detection limits by biobarcode and closely related approaches
•Conclusion
|
Alam, Principles of Nanobiosensors, 2013 |
3 |
A ‘Mendeleev table’ for biosensors
|
aM |
fM |
|
|
pM |
|
|
|
|
|
|
|
|
|
|
nM |
µM |
|
|
|
|
|
|
mM |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Alam, Principles of Nanobiosensors, 2013 |
4 |
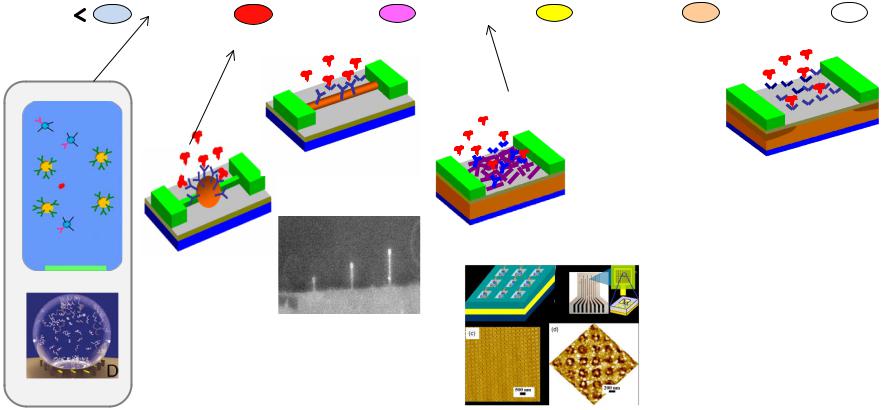
Strategies to beat the diffusion limit
|
τ ~ L2 |
|
|
D |
|
Fragment |
Reduce |
Generate |
the space |
the space |
locally |
Magnetic |
Droplet |
Ion torrent |
biobarcode |
evaporation |
approach |
All can achieve sub-fM detection in reasonable time |
5 |