4.2. Решение примера
Для точки на плоскости заданы законы изменения во времени ее координат:
.
Найти
траекторию точки; для момента времени
определить
ее положение, вычислить скорость и
ускорение, а так же их проекции на оси
декартовой и естественной координатных
систем, радиус кривизны траектории;
все вычисленные величины нанести на
рисунок.
Решение. Для получения уравнения траектории исключим время из заданных уравнений
.
Полученное
выражение описывает параболу с
направленными вниз ветвями, вершина
параболы сдвинута вдоль оси y
вверх на единицу. Однако анализ выражений
для координат показывает, что
,
в этом случае траекторией точки является
только часть параболы (см. рисунок 6).
Определим положение точки в заданный момент времени:
.
Найдем проекции скорости на оси декартовой координатной системы:
;
В
декартовой координатной системе вектор
скорости записывается как
,
где
- единичные орты координатных осей x
и y,
а в естественной координатной системе
как
,
где
и
- единичные орты касательной и главной
нормали к траектории в рассматриваемой
точке. Очевидно, что в таком случае
.
Найдем проекции ускорения на оси декартовой координатной системы и его величину:
;
.
При
этом
.
Найдем проекции ускорения на оси естественной координатной системы как
При
этом
.Нанесем
вычисленные величины на рисунок; при
этом выберем масштаб для скорости: в 1
– 1.5
,
а масштаб для ускорения: в 1
– 4
.
Вычислим радиус кривизны траектории в рассматриваемой точке как
.
С решением подробных примеров можно ознакомиться, например, в [2,4,5].
Задание 5. Кинематика плоского движения тела
5.1. Краткие сведения из курса механики
Движение твердого тела называется плоскопараллельным (плоским), если все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Частными случаями плоского движения являются поступательное плоское движение и вращение вокруг неподвижной оси.
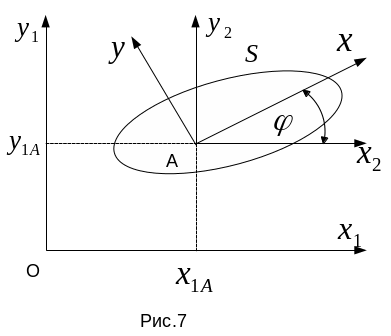
Для
описания (задания) движения плоской
фигуры в неподвижной системе отсчета
введем жестко связанную с фигурой
координатную систему
,
а так же полусвязанную поступательно
движущуюся координатную систему
,
оси которой параллельны соответствующим
осям неподвижной системы отсчета (см.
рисунок 7).
Тогда
положение фигуры
на неподвижной плоскости
определяется функциями
(27)
которые называются уравнениями движения плоской фигуры или уравнениями плоскопараллельного движения твердого тела.
Наиболее
распространено рассмотрение плоского
движения как результат сложения двух
более простых движений. Первое из них
происходит вместе с полусвязанной
системой
(поступательное движение с кинематическими
характеристиками точки
,
называемой в этом случае полюсом),
а второе представляет собой вращение
вместе с осями связанной системы
относительно полусвязанной (вращение
вокруг полюса). В такой трактовке,
называемой методом
полюса,
первое уравнение в (27) определяет движение
полюса, а второе описывает вращение
плоской фигуры вокруг полюса (точнее,
вокруг оси
).
Выбор в качестве полюса другой точки
изменяет поступательное движение
полусвязанной координатной системы;
при этом глобальные кинематические
характеристики вращательного движения
остаются прежними (инвариантными
относительно выбора полюса).
Выражение
для расчета скорости любой точки
(например, точки
)
методом полюса:
,
(28)
Выражение для расчета ускорения точки методом полюса:
.
(29)
Второе
и третье слагаемые являются, соответственно,
вращательной (
) и осестремительной (
)
составляющими ускорения точки
при вращении плоской фигуры вокруг
полюса А .
Тогда формулу (29) можно записать так
.
(30)
В
том случае, когда за полюс выбрана точка
,
скорость которой равна нулю, выражение
(28) приобретает наиболее простой и
удобный для расчета вид:
.
(31)
Это означает, что скорости точек при плоскопараллельном движении тела можно определять так же, как и в случае вращения тела вокруг неподвижной оси. Однако при этом ось вращения движется; в каждый момент времени она перпендикулярна плоскости фигуры и проходит через точку . Она называется мгновенной осью вращения тела, а точка - мгновенным центром скоростей (м.ц.с.) плоской фигуры. В некоторых случаях существование и положение такой точки очевидно. Так, если колесо катится без скольжения по горизонтальной поверхности, то равна нулю скорость той точки колеса, которая соприкасается с неподвижной поверхностью.
В некоторых случаях удобно использовать следующее полезное свойство: проекции скоростей точек твердого тела на прямую, проходящую через эти точки, равны между собой.
Более подробно с материалом можно ознакомиться, например, в [1,4,5].