Задание 2. Применение теоремы об изменении кинетического момента для определения угловой скорости вращающегося тела
2.1. Краткие сведения из курса механики
2.1.1. Понятие кинетического момента
Момент количества движения материальной точки массы относительно выбранного центра называется ее кинетическим моментом
(4)
здесь
– радиус-вектор точки относительно
неподвижного центра О,
– скорость точки.
Кинетическим
моментом
механической системы относительно
центра О называется геометрическая
сумма (главный момент) количеств движения
составляющих эту систему материальных
точек относительно этого же центра О:
(5)
Проецируя (5) на
оси неподвижной декартовой системы
координат
,
получим выражения для соответствующих
проекций (иногда их называют моментами
количеств движения относительно
соответствующих осей):
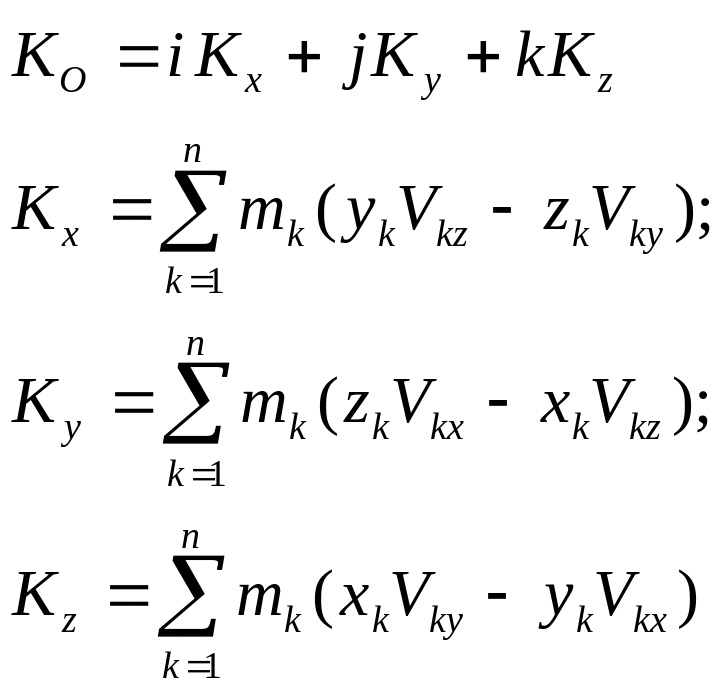(6)
Для механических систем с непрерывным распределением массы в выражениях (5, 6) суммирование следует заменить интегрированием.
Кинетический момент системы, вычисленный относительно неподвижного центра О (его проекция на ось, проходящую через точку О), является векторной мерой, характеризующей вращение механической системы относительно неподвижного центра (оси).
В качестве примера запишем кинетический момент тела при его вращении вокруг неподвижной точки.
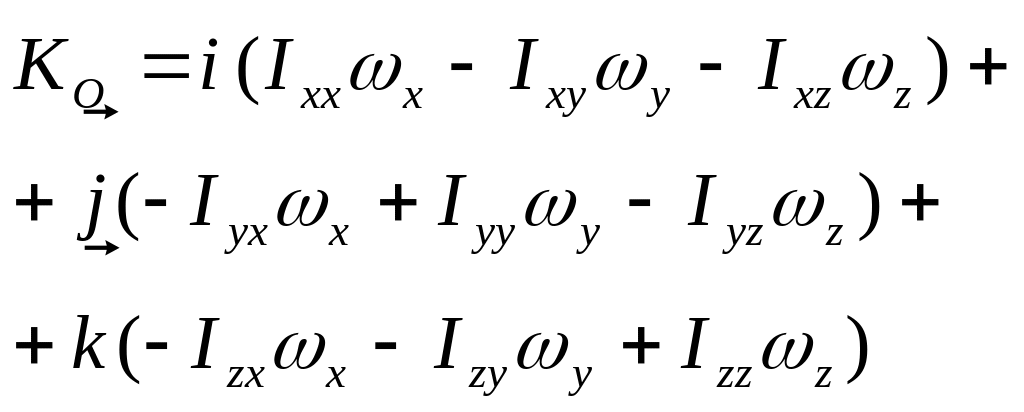(7)
Величины
;
;
называются
моментами инерции тела
относительно осей
,
и
,
или осевыми моментами инерции,
соответственно, а
;
;
– центробежными
моментами инерции твердого тела. Все
эти величины характеризуют инерционные
свойства тела при вращении. Они являются
характеристиками распределения массы
в твердом теле. Для однородных тел, у
которых плотность
постоянна, соотношения между моментами
инерции определяются только формой
тела и расположением координатных осей
.
Более подробные сведения о моментах
инерции изложены в [1, 3, 4] .
В частном случае,
когда тело вращается вокруг неподвижной
оси
и
,
кинетический момент тела определяется
выражением
(8)
2.1.2. Теорема об изменении кинетического момента относительно неподвижного центра.
Выражение
(9)
является математической записью теоремы об изменении кинетического момента механической системы относительно неподвижного центра О: производная по времени от кинетического момента механической системы, вычисленного относительно неподвижного центра, равна главному моменту внешних сил относительно этого центра.
Проецируя (9) на оси декартовой координатной системы , получим
,
,
(10)
Из формулы (10) следует, что если главный момент внешних сил окажется равным нулю, то на рассматриваемом интервале времени кинетический момент механической системы не изменяется.
Если окажется, что равна нулю проекция на какую-либо координатную ось главного момента внешних сил, то будет постоянной проекция на эту ось вектора кинетического момента механической системы.
2.1.3. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Пусть твердое тело
вращается вокруг неподвижной оси
;
закон изменения во времени угла поворота
задан. Из (8) найдем проекцию вектора
кинетического момента на ось вращения
и подставим ее в третье уравнение из
(10). Окончательно имеем:
или
(11)
где
и
– угловое ускорение и угловая скорость
вращения. Выражение (11) является
дифференциальным уравнением первого
порядка относительно угловой скорости
вращения, либо дифференциальным
уравнением второго порядка относительно
угла поворота тела.
Более подробно с материалом можно ознакомиться, например, в [1, 3, 4].