
- •Порядок и правила выполнения контрольных работ
- •В арианты контрольных работ, выполняемые на первом курсе
- •Контрольная работа № 1 «Элементы алгебры и геометрии»
- •Контрольная работа № 2 «Производная и дифференциал»
- •Контрольная работа № 3 «Техника интегрирования и приложения определенного интеграла»
- •Перечень вопросов, выносимых на экзамен
- •Рекомендуемая литература
Контрольная работа № 1 «Элементы алгебры и геометрии»
В
задачах 1 –
20 найти
матрицу
![]() .
.
1. 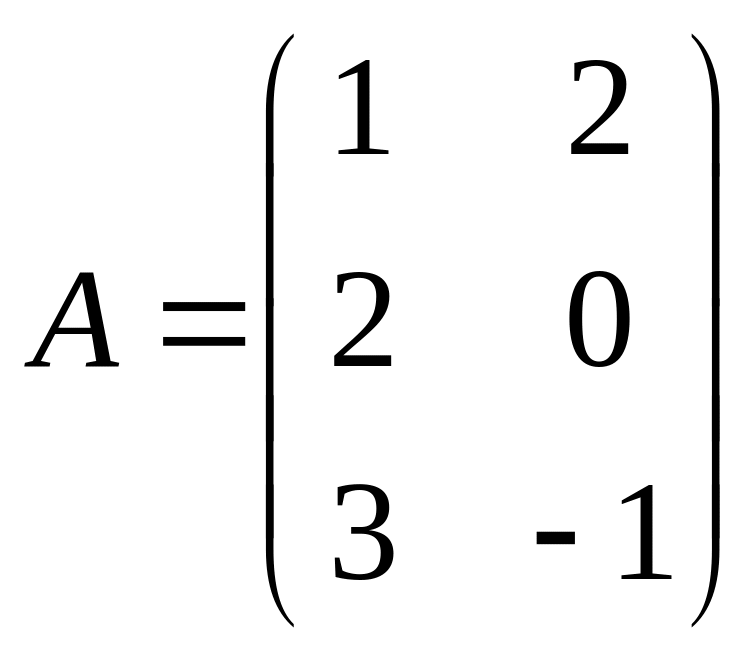 ,
,
![]() ,
,
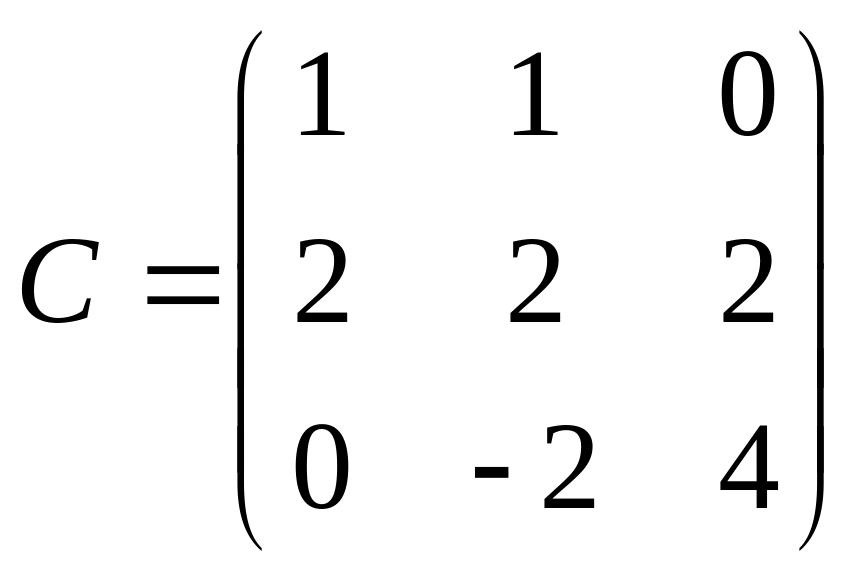 .
.
2. 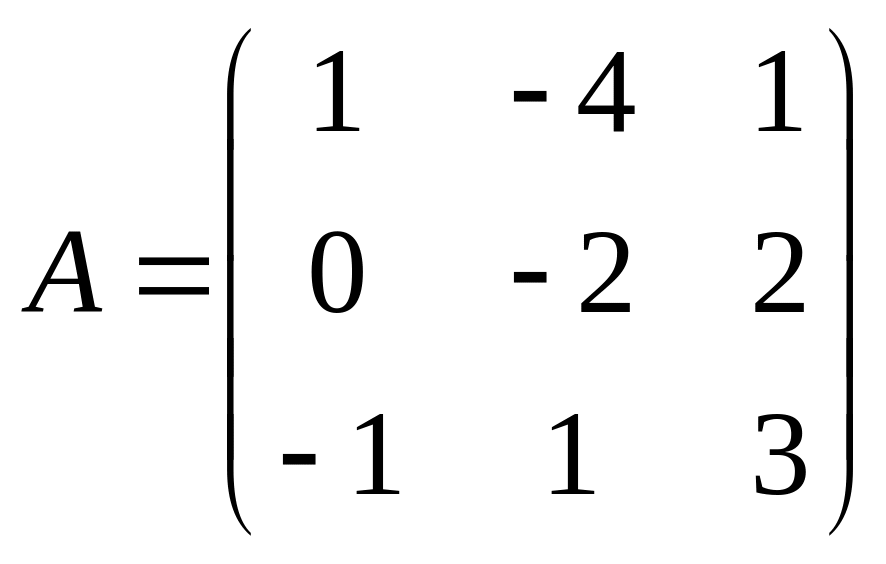 ,
,
 ,
,
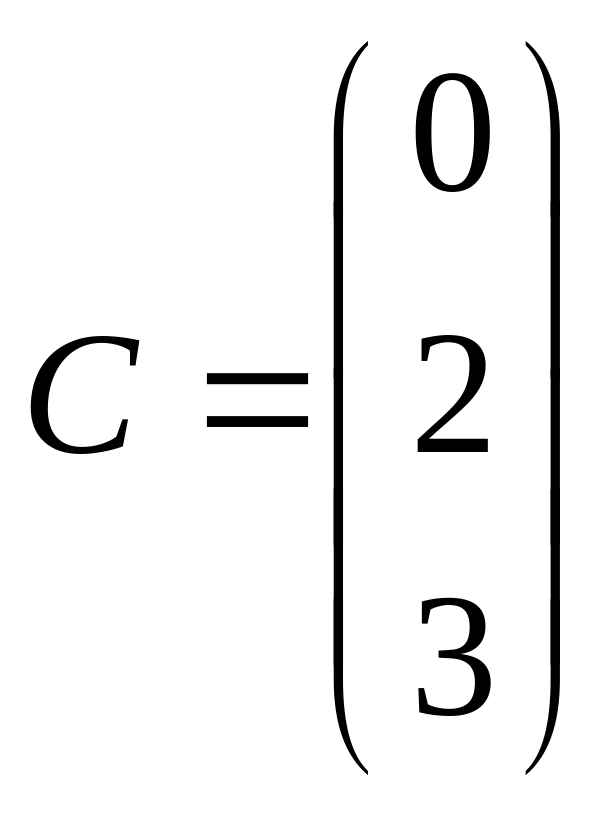 .
.
3. ![]() ,
,
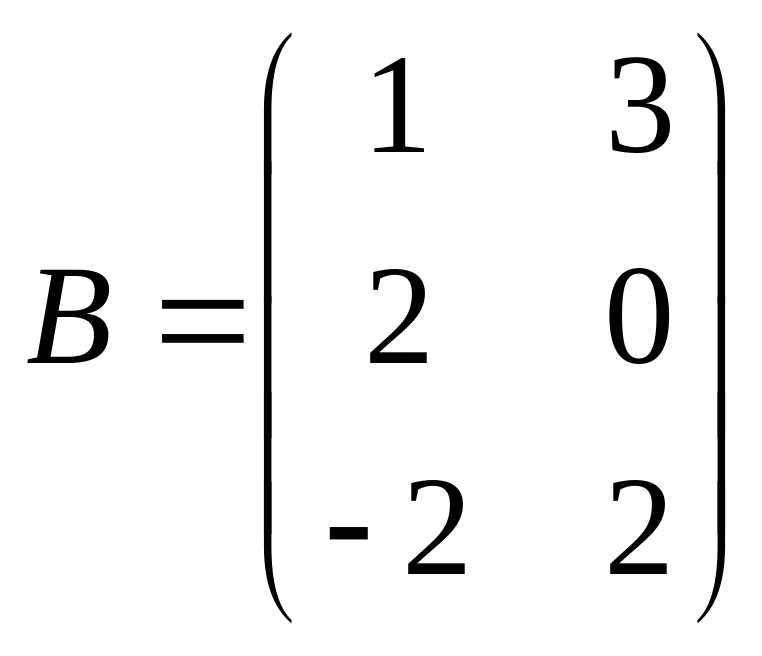 ,
,
![]() .
.
4. ![]() ,
,
![]() ,
,
![]() .
.
5. 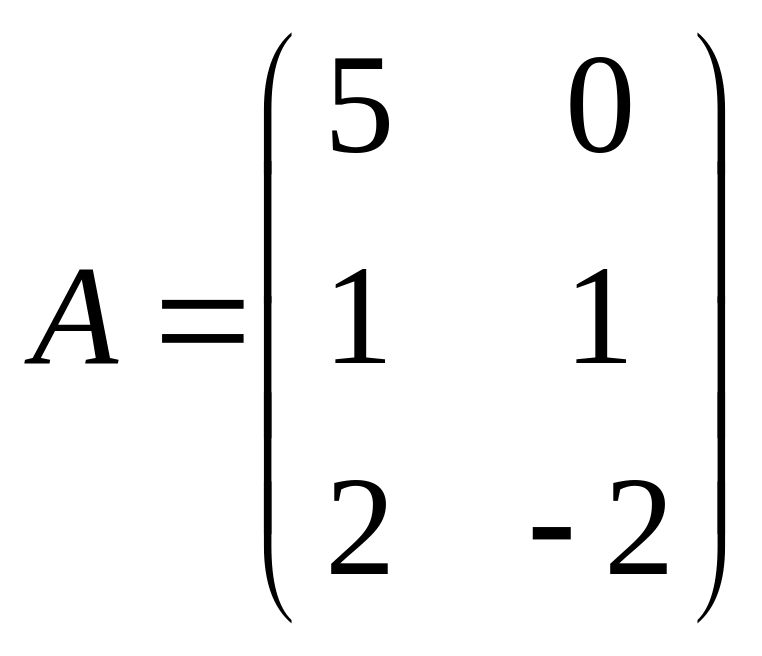 ,
,
![]() ,
,
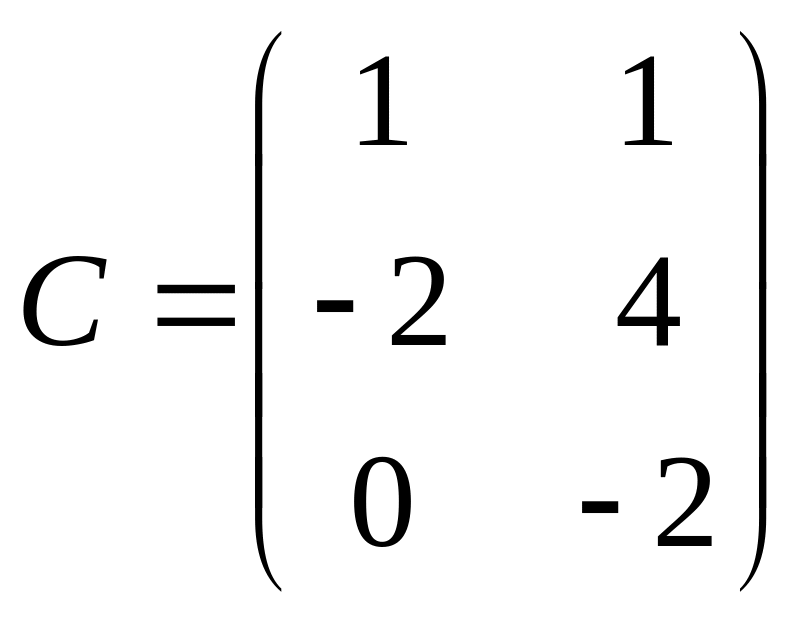 .
.
6. 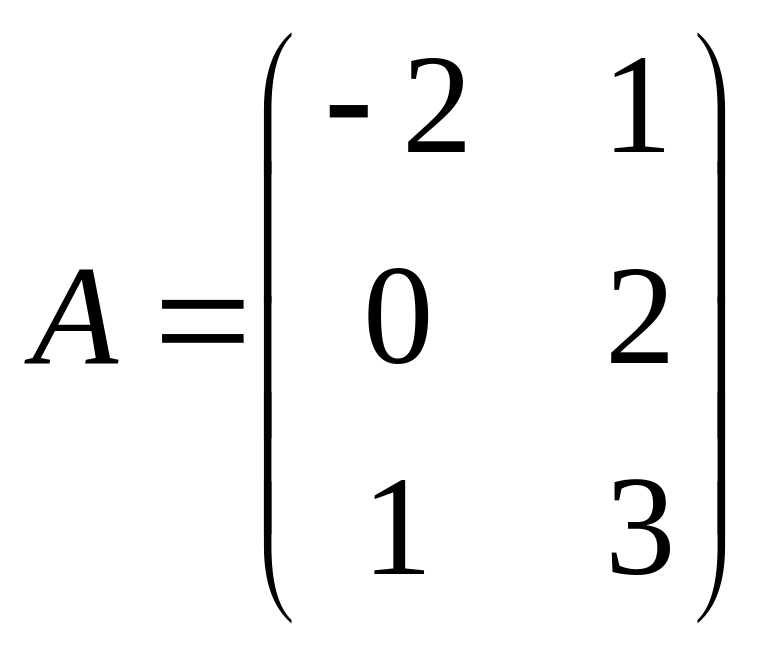 ,
,
![]() ,
,
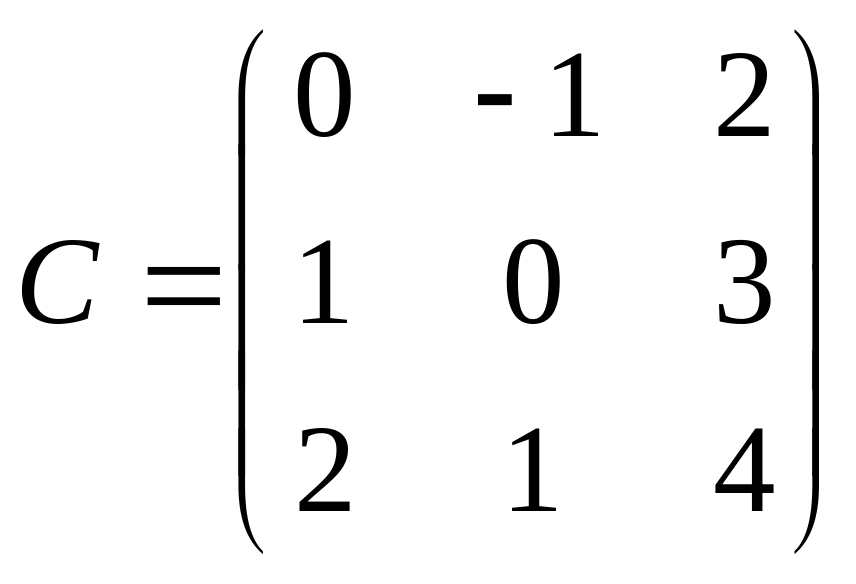 .
.
7. 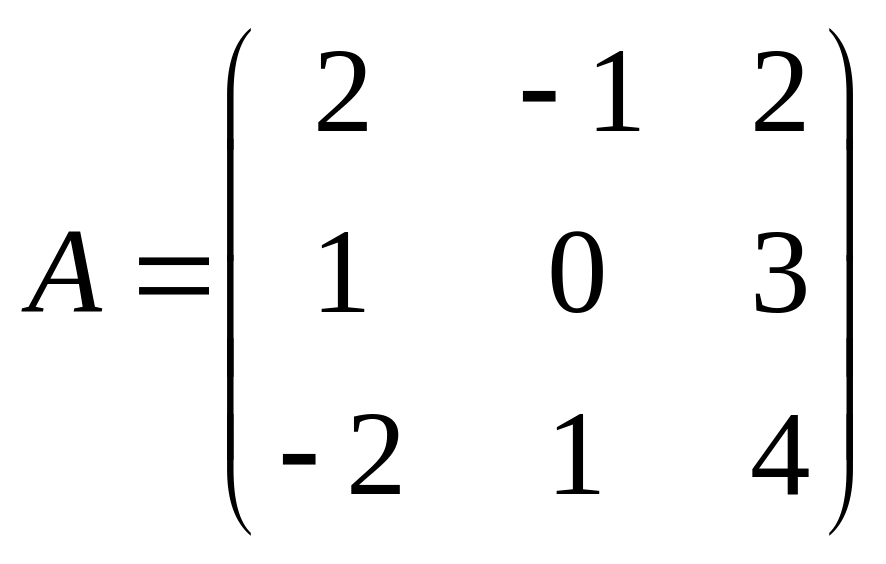 ,
,
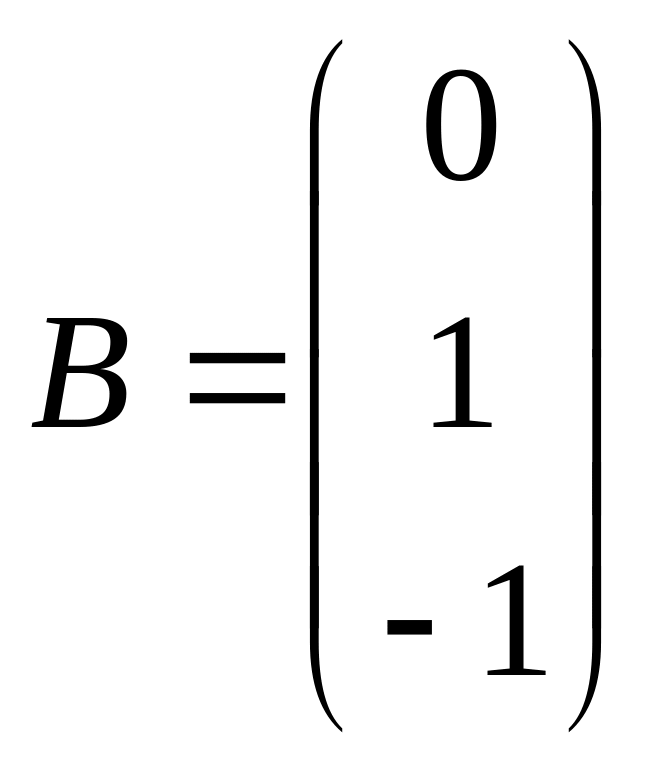 ,
,
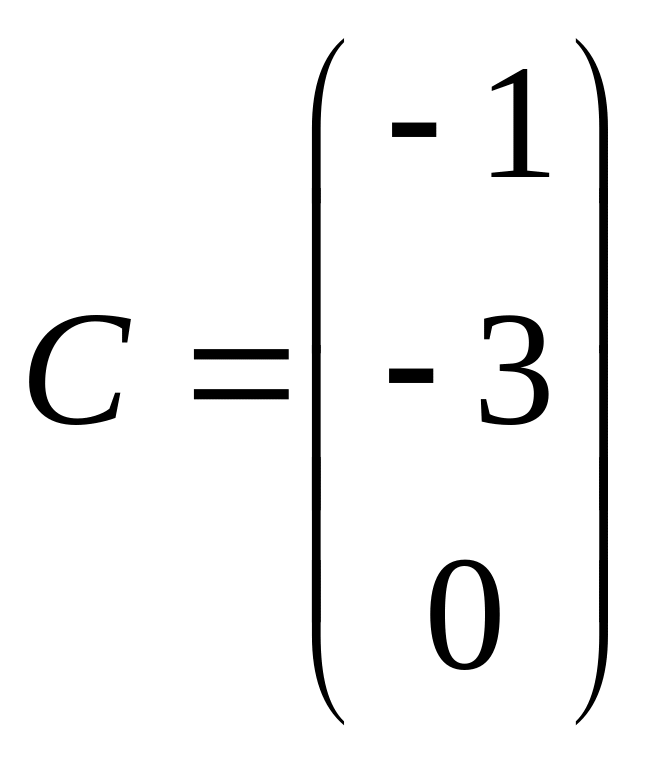 .
.
8. ![]() ,
,
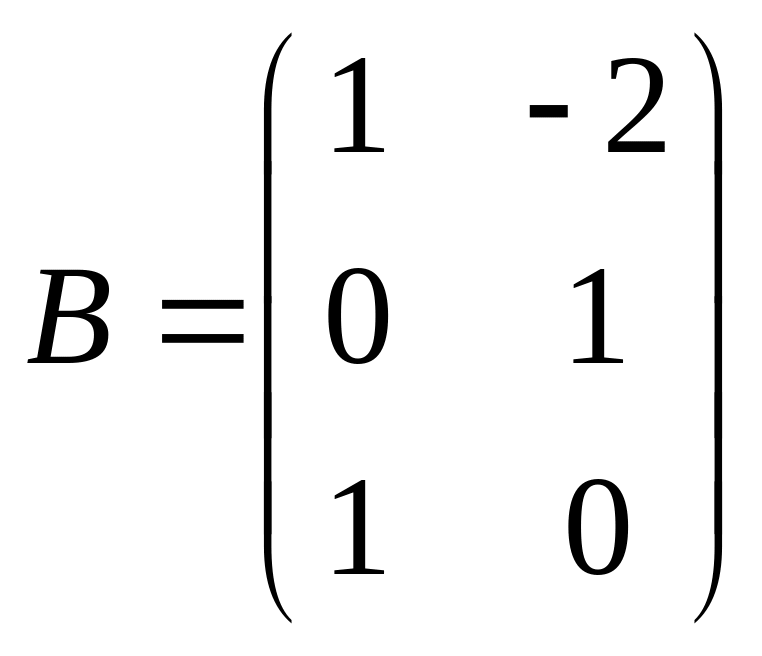 ,
,
![]() .
.
9. ![]() ,
,
![]() ,
,
![]() .
.
10. 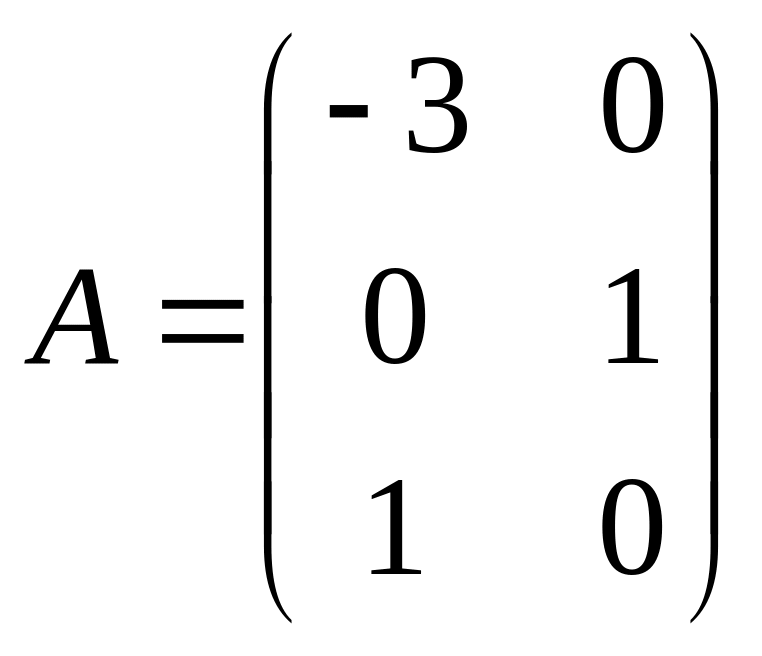 ,
,
![]() ,
,
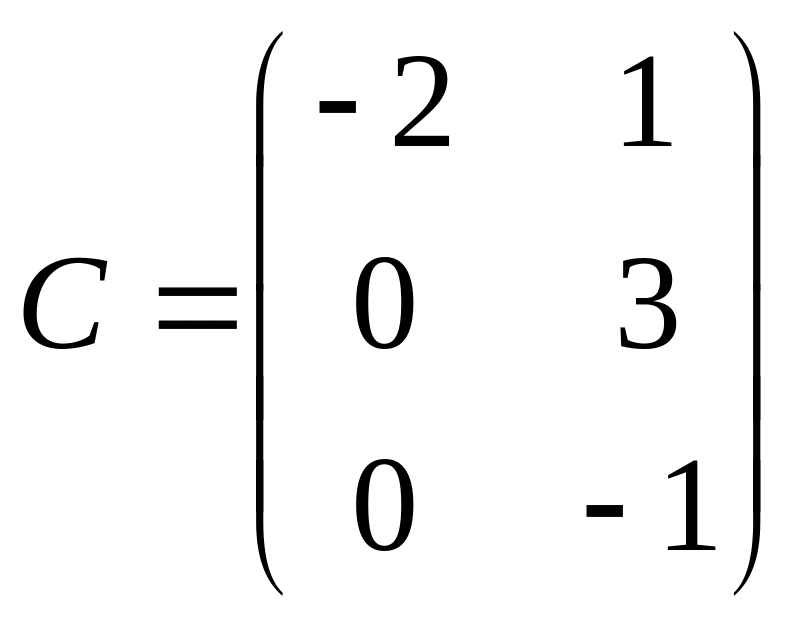 .
.
11. 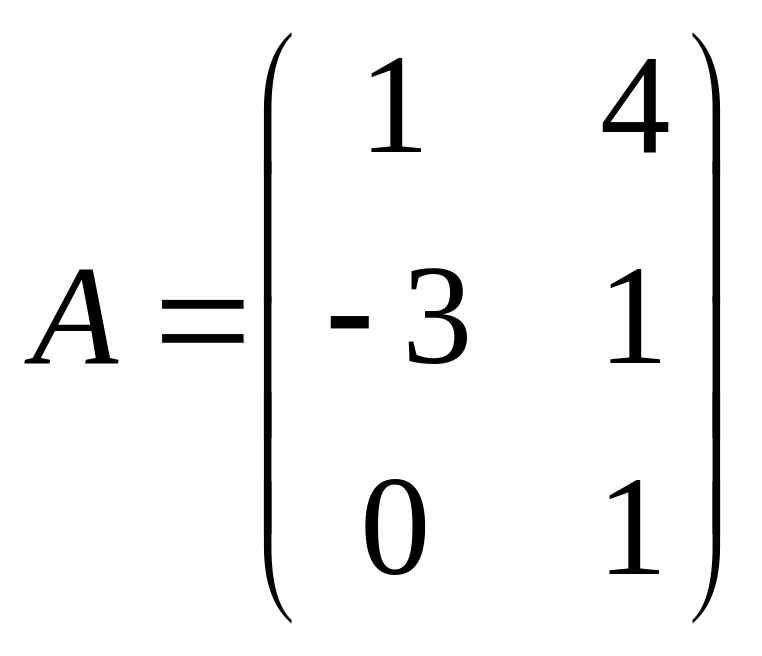 ,
,
![]() ,
,
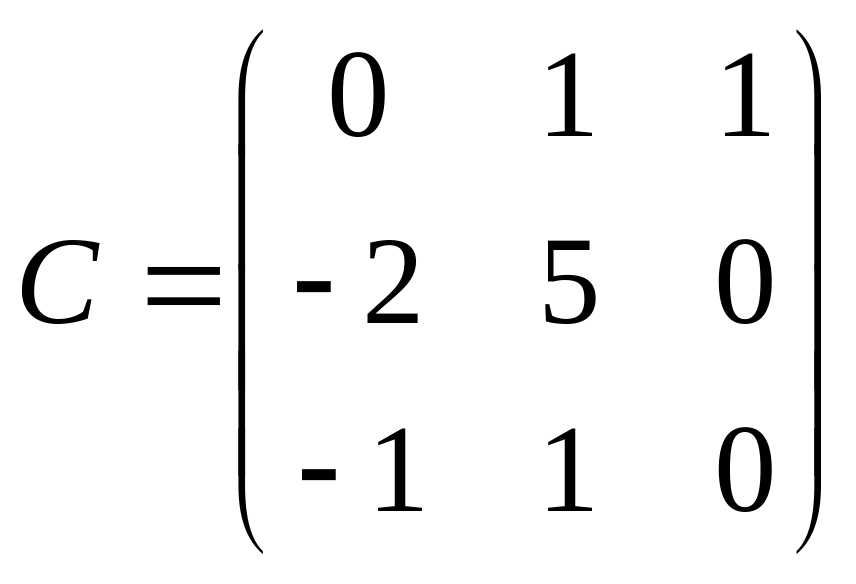 .
.
12. 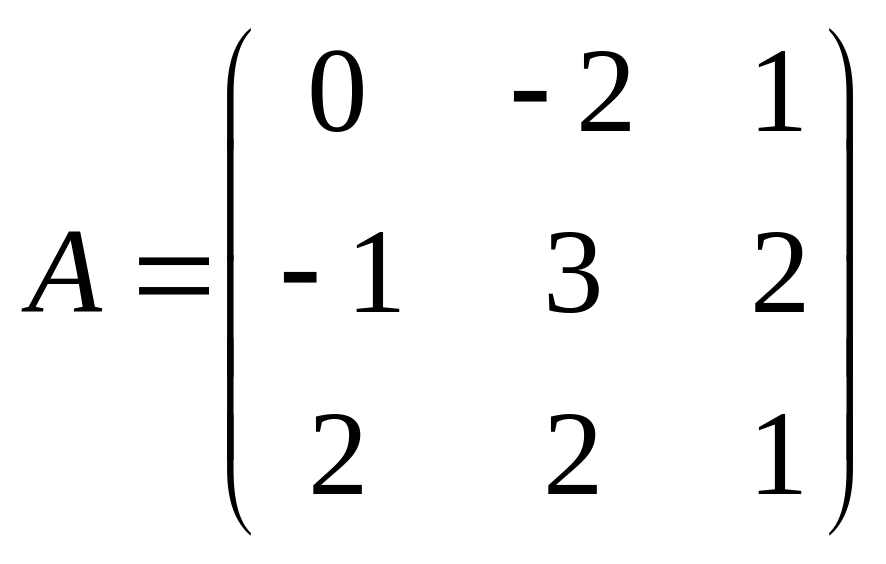 ,
,
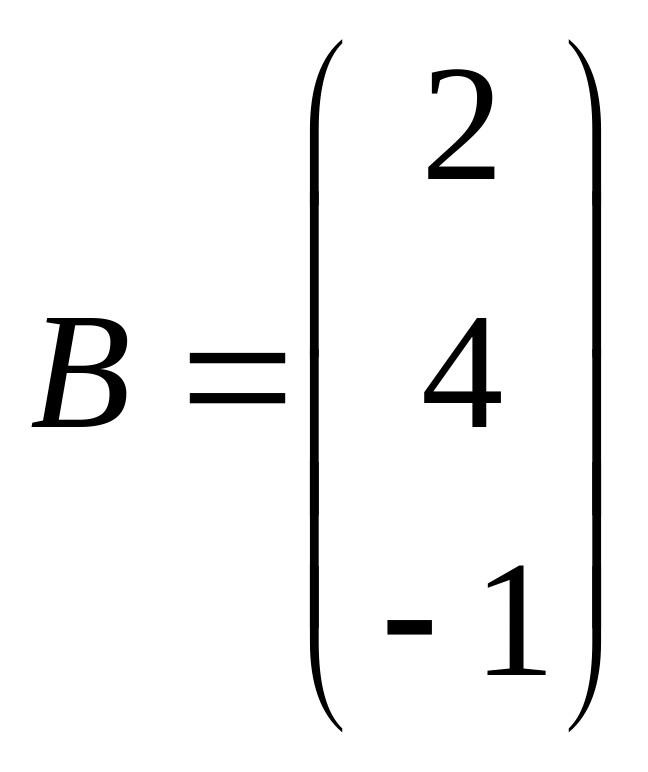 ,
,
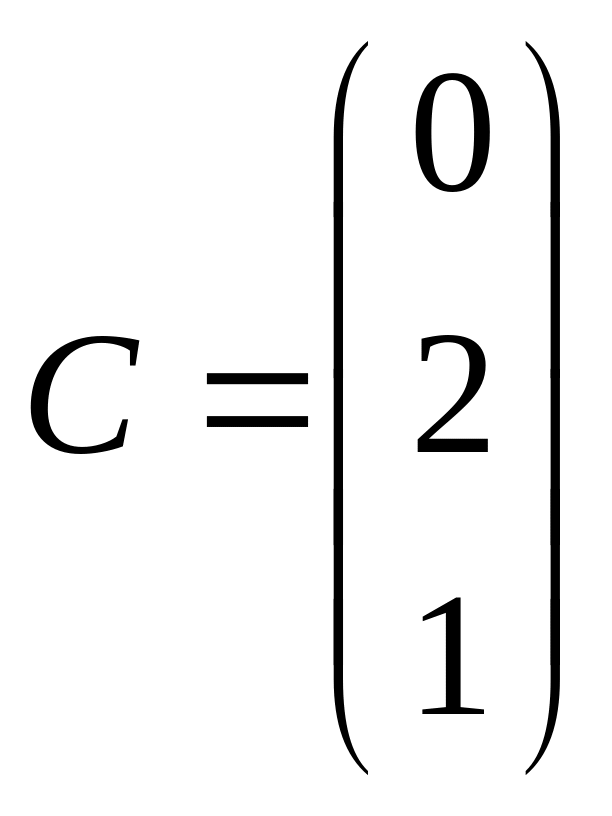 .
.
13. ![]() ,
,
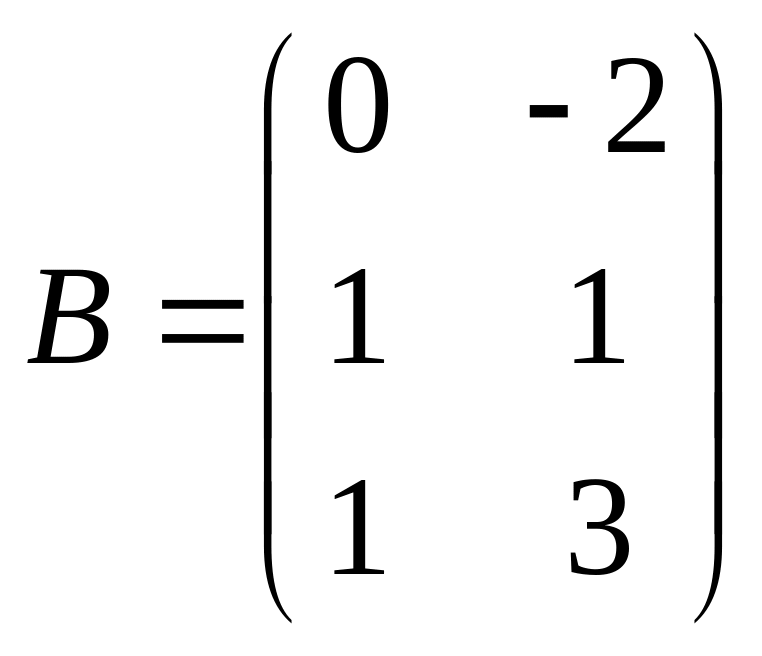 ,
,
![]() .
.
14. ![]() ,
,
![]() ,
,
![]() .
.
15. 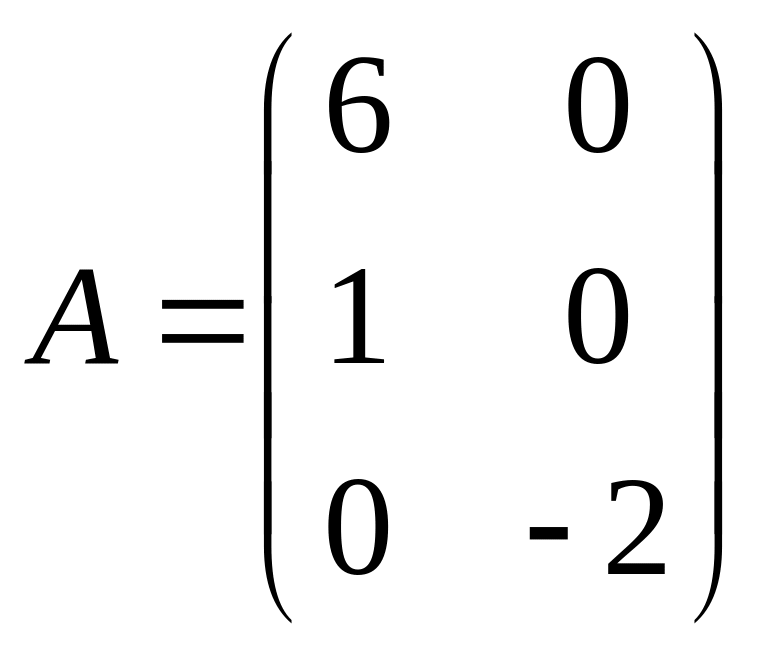 ,
,
![]() ,
,
 .
.
16. 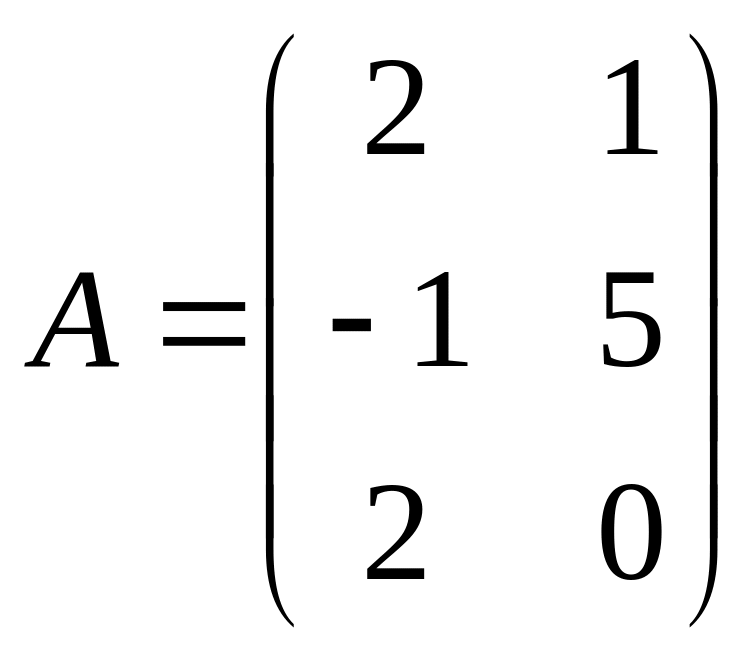 ,
,
![]() ,
,
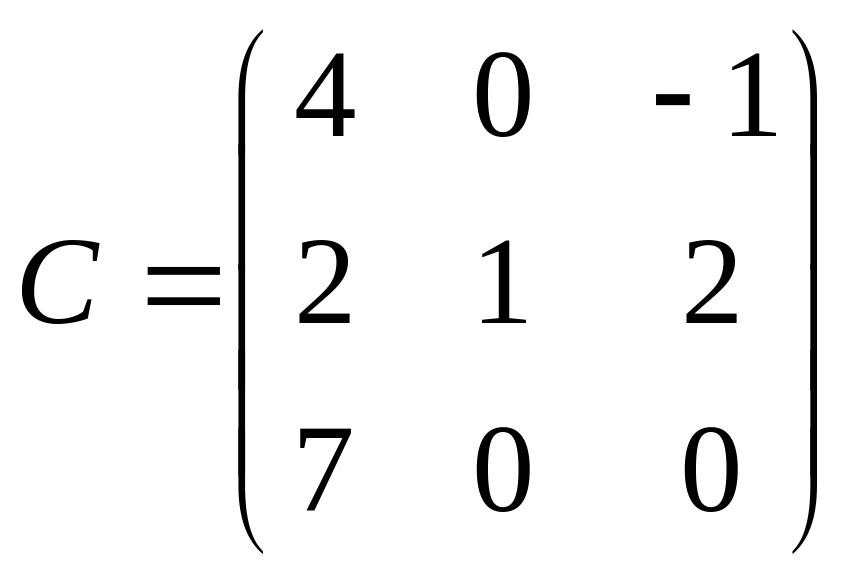 .
.
17. 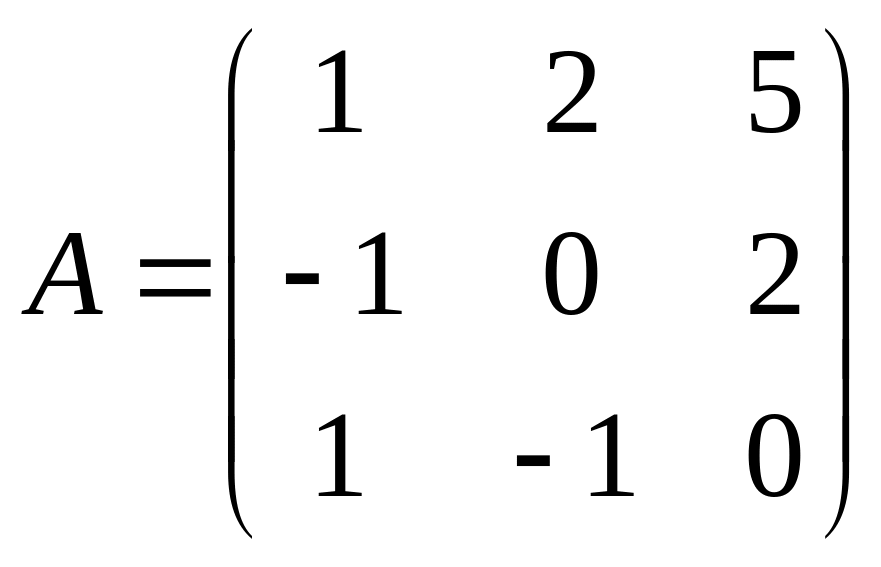 ,
,
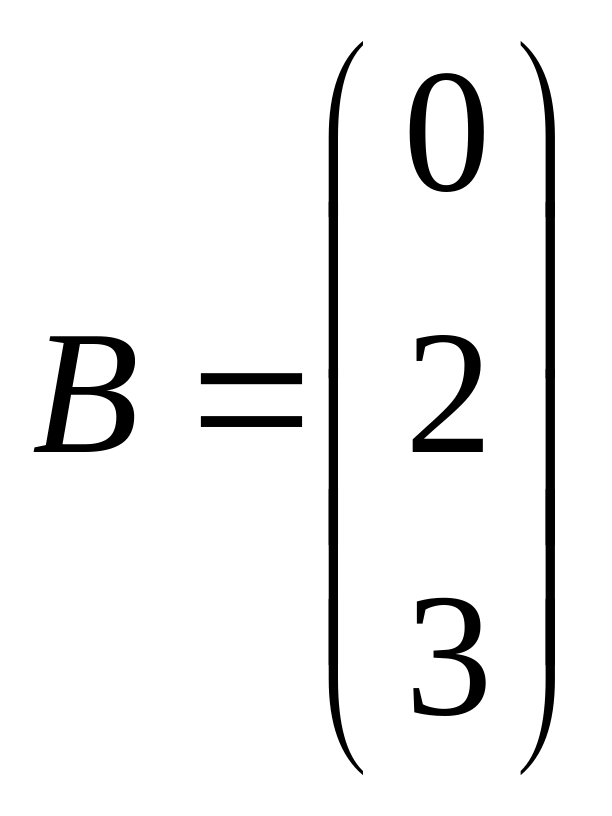 ,
,
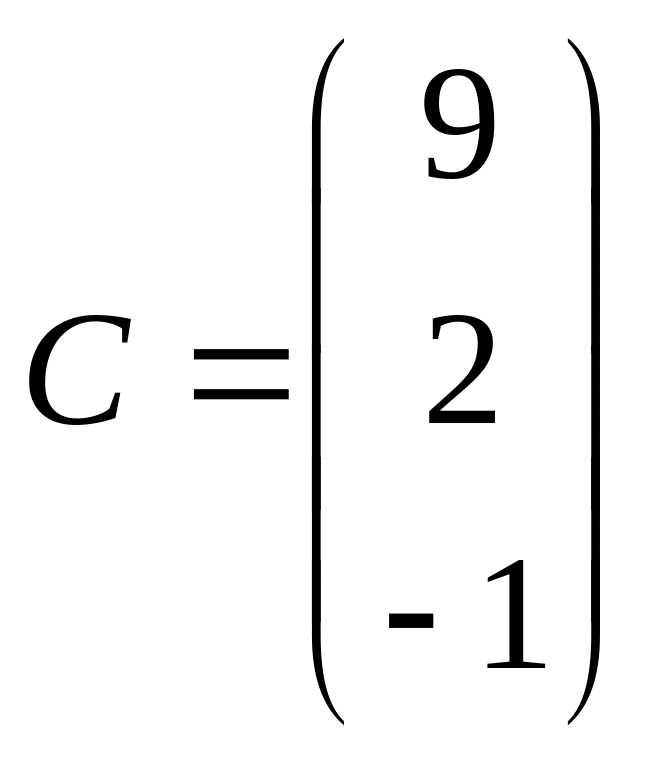 .
.
18. ![]() ,
,
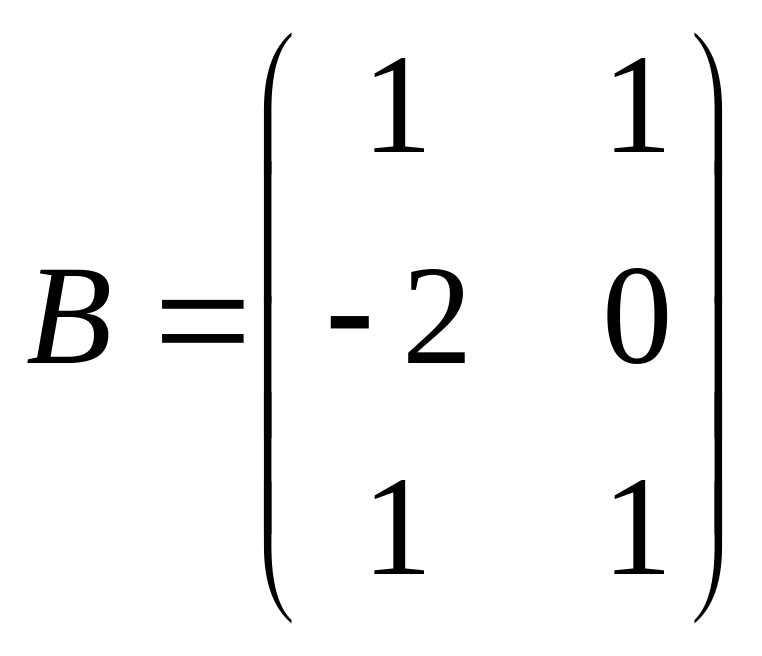 ,
,
![]() .
.
19. ![]() ,
,
![]() ,
,
![]() .
.
20. 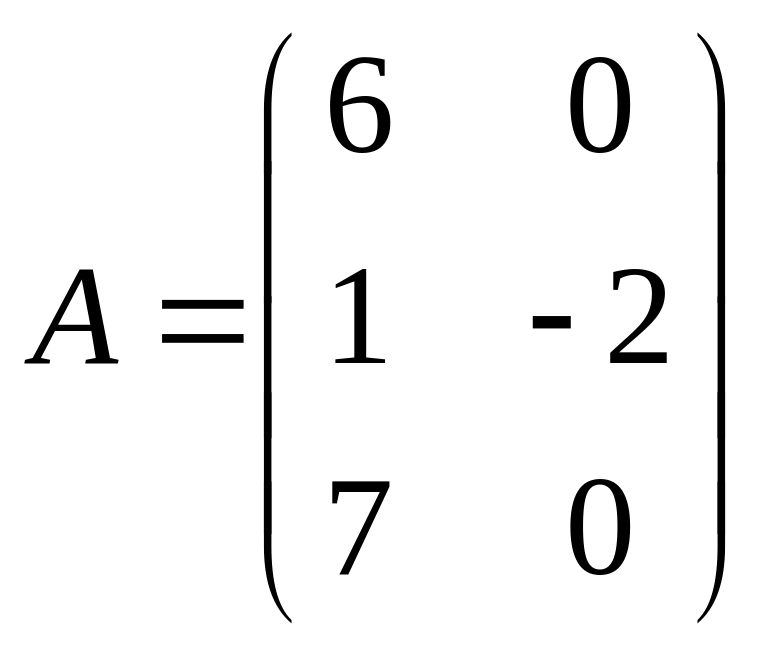 ,
,
![]() ,
,
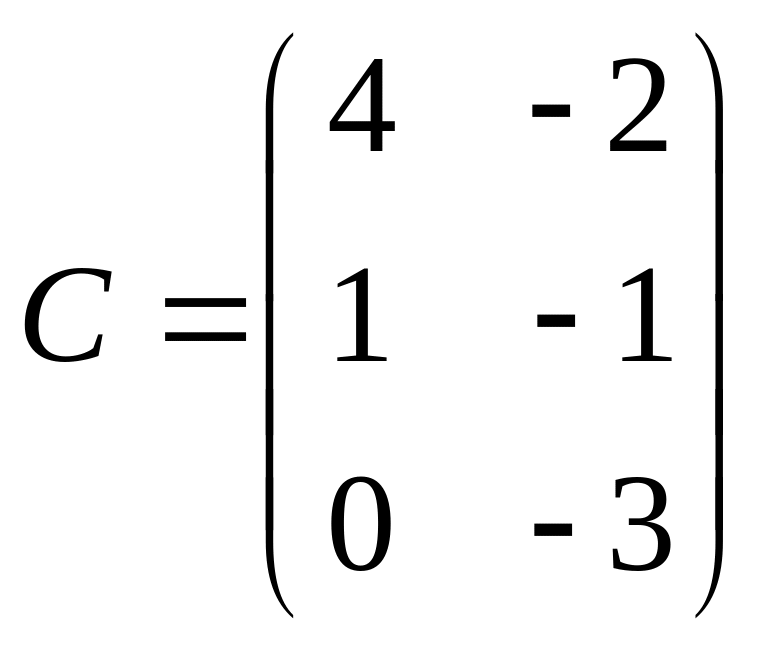 .
.
В
задачах 21 –
40 дана
невырожденная матрица
![]() .
Найти обратную матрицу
.
Найти обратную матрицу
![]() и пользуясь правилом умножения матриц,
показать, что
и пользуясь правилом умножения матриц,
показать, что
![]() ,
где
,
где
![]() – единичная матрица.
– единичная матрица.
21. 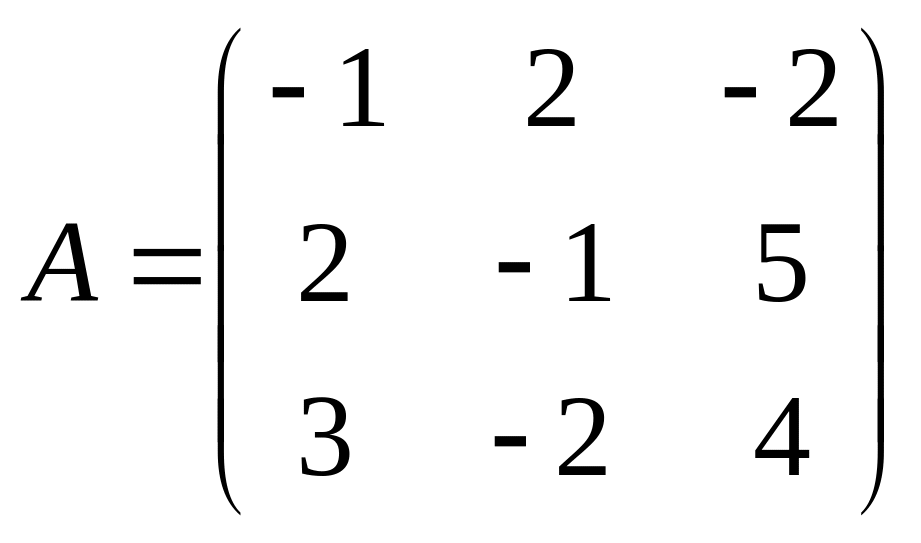 . 22.
. 22. 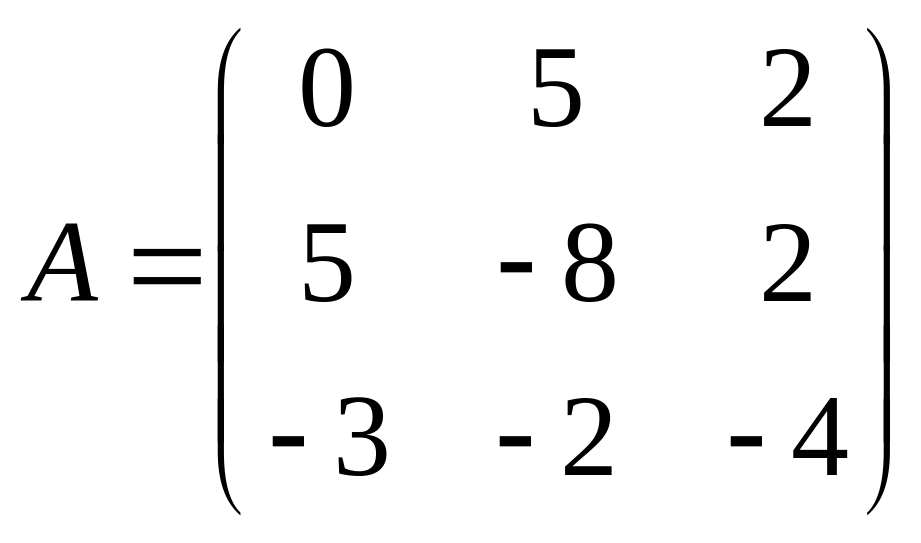 . 23.
. 23. 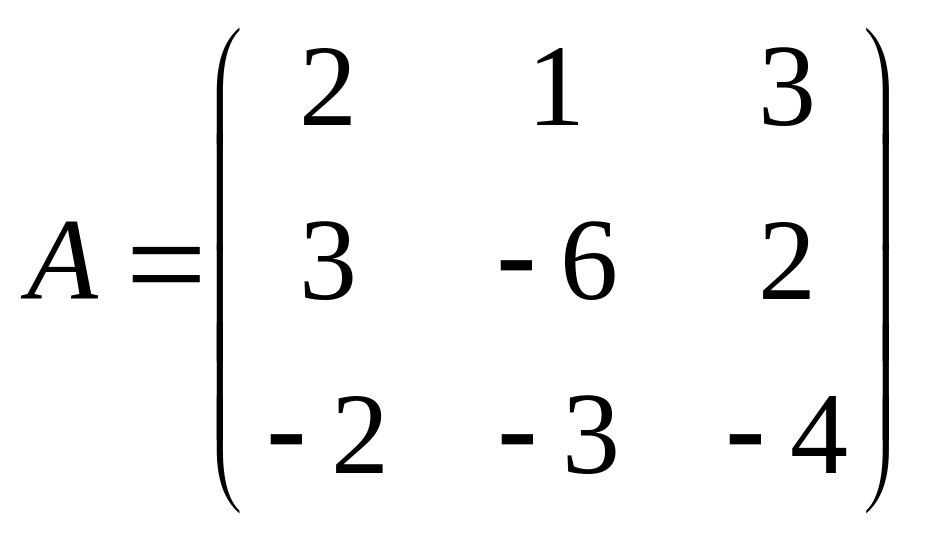 .
.
24. 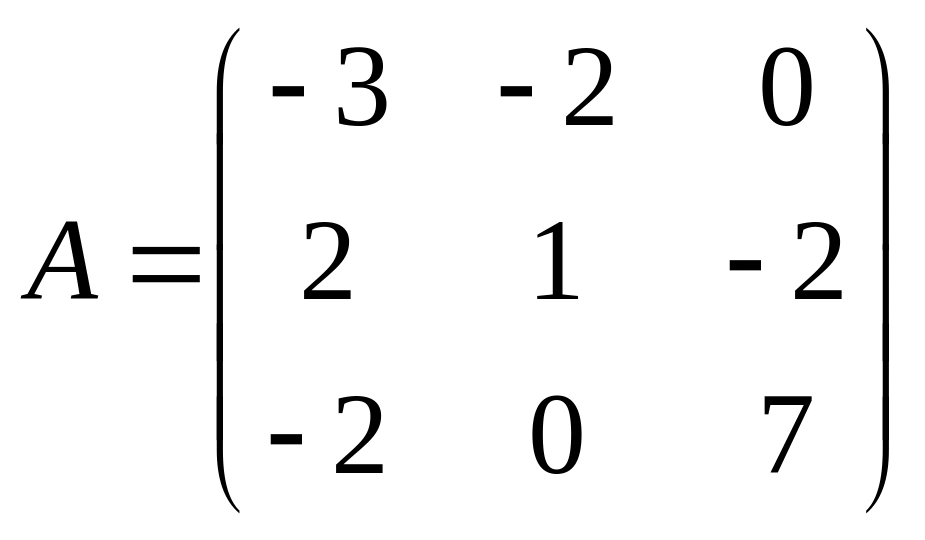 . 25.
. 25. 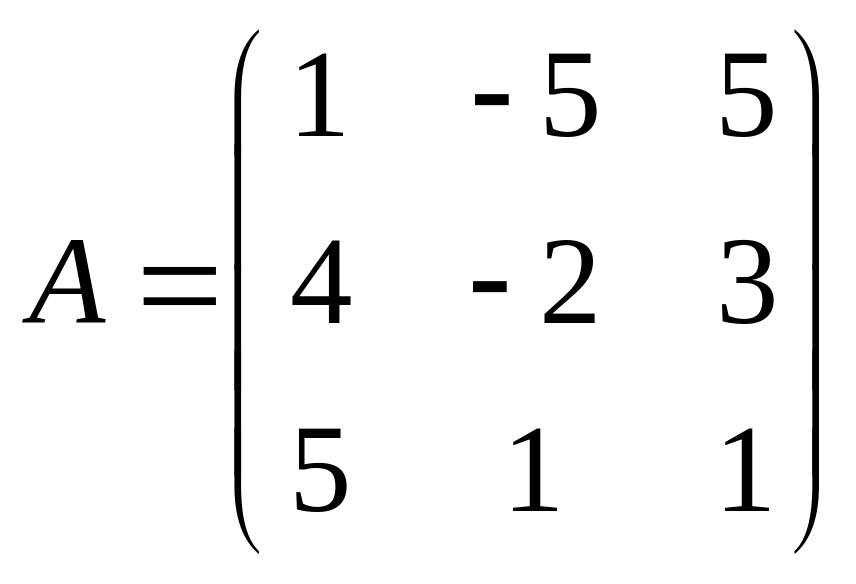 . 26.
. 26. 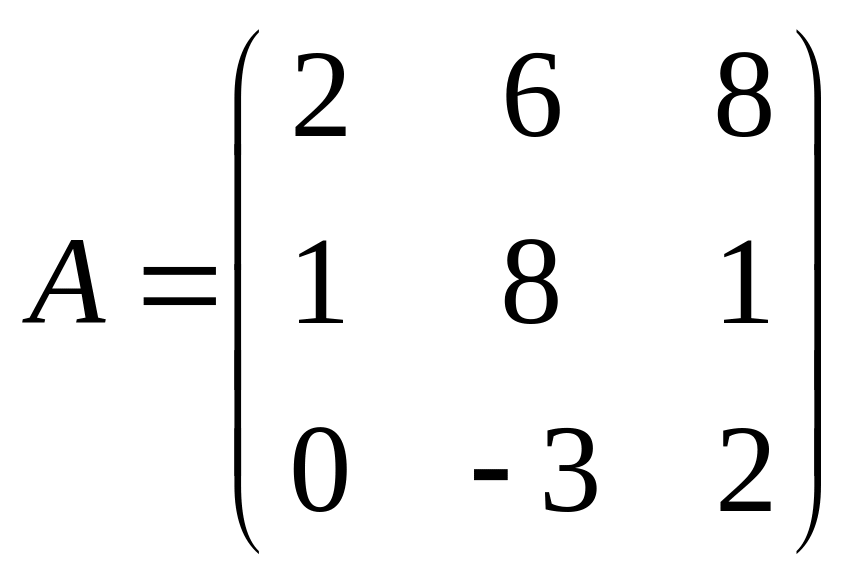 .
.
27. 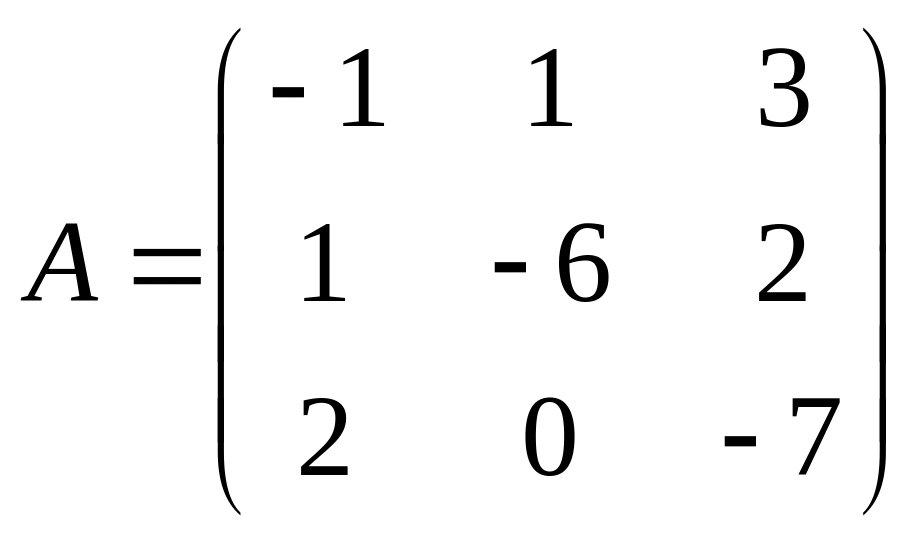 . 28.
. 28. 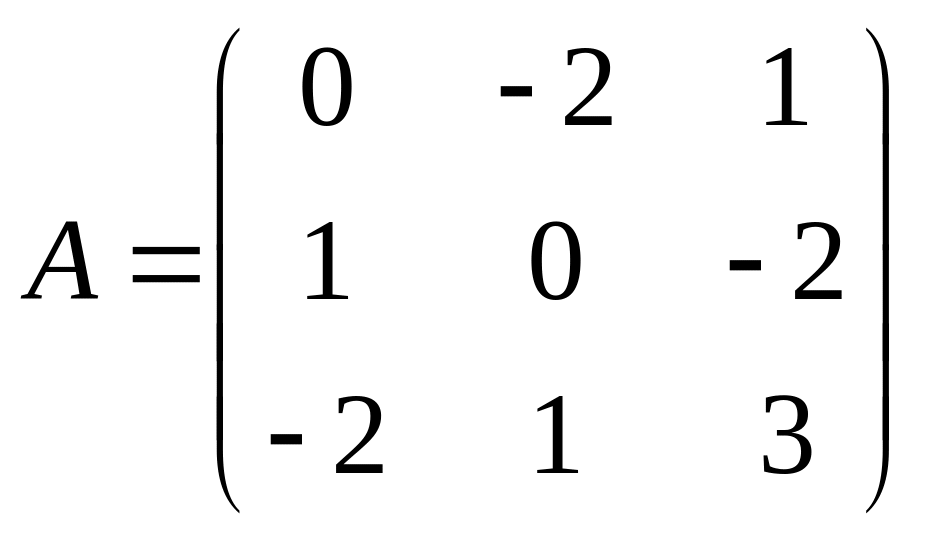 . 29.
. 29. 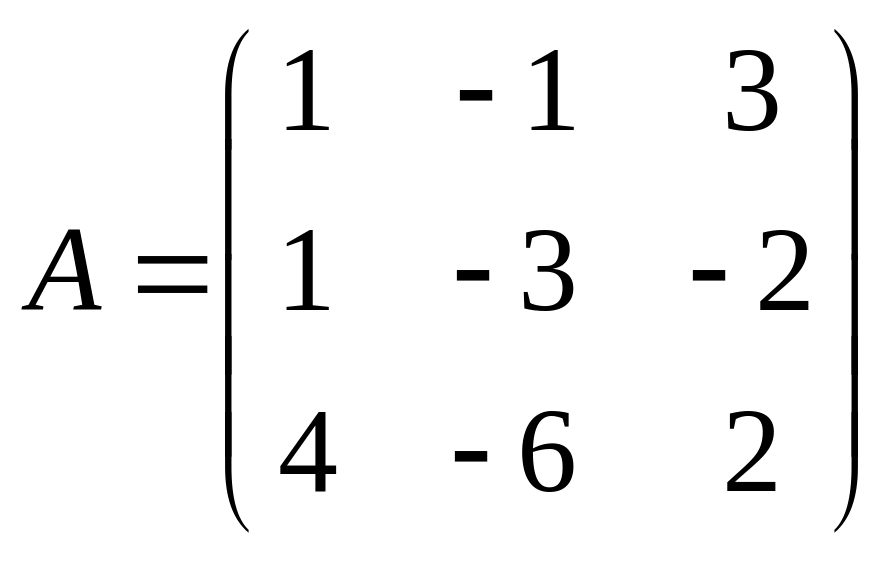 .
.
30. 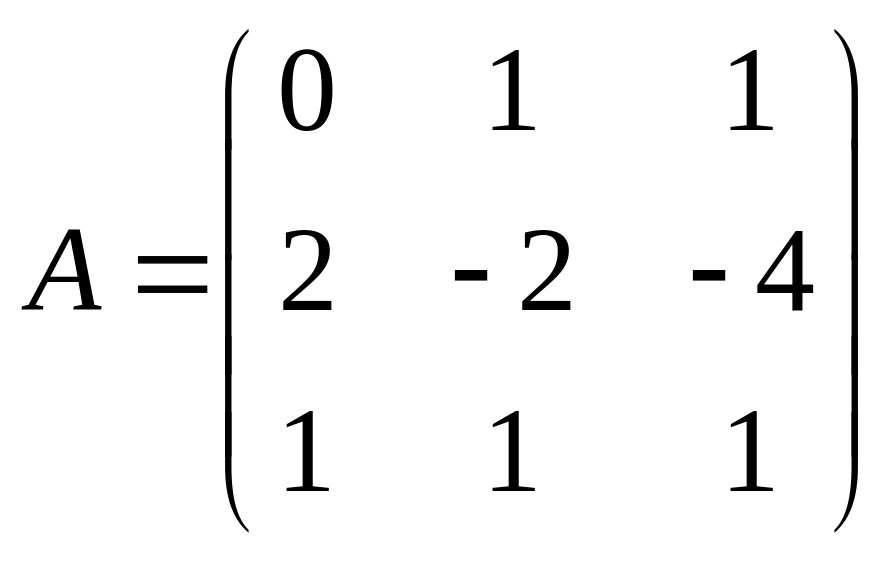 . 31.
. 31. 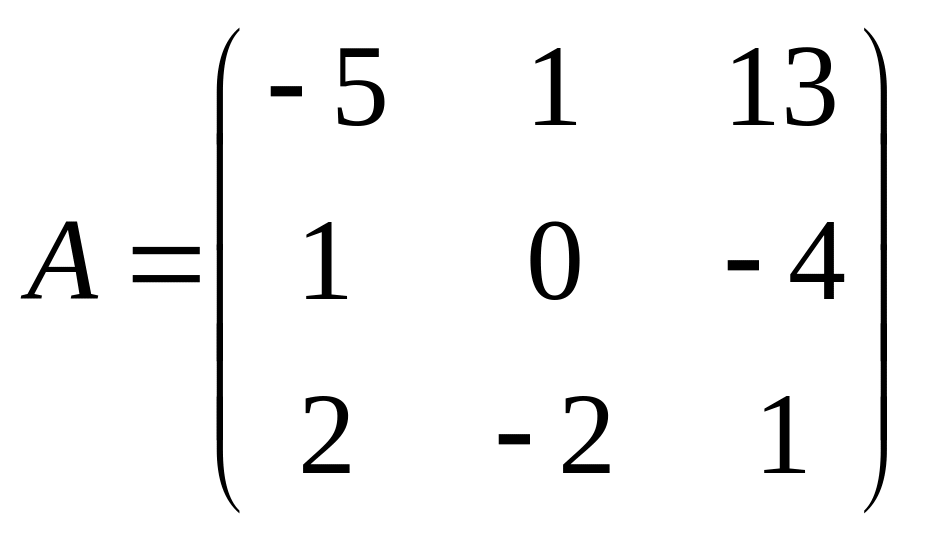 . 32.
. 32.  .
.
33. 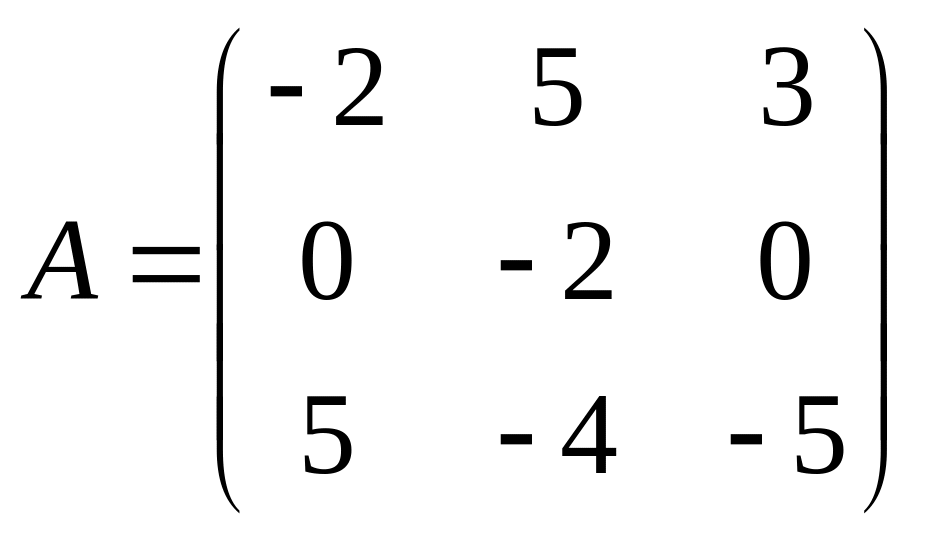 . 34.
. 34. 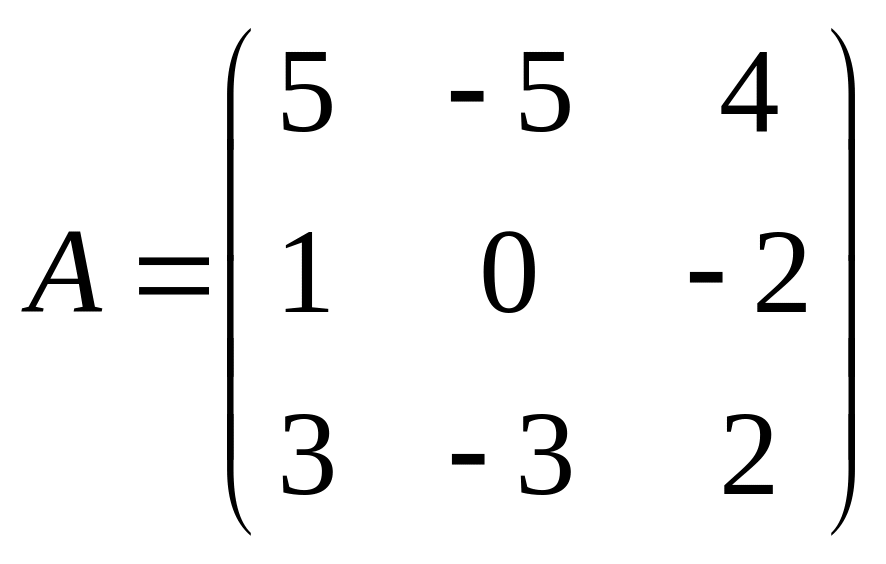 . 35.
. 35. 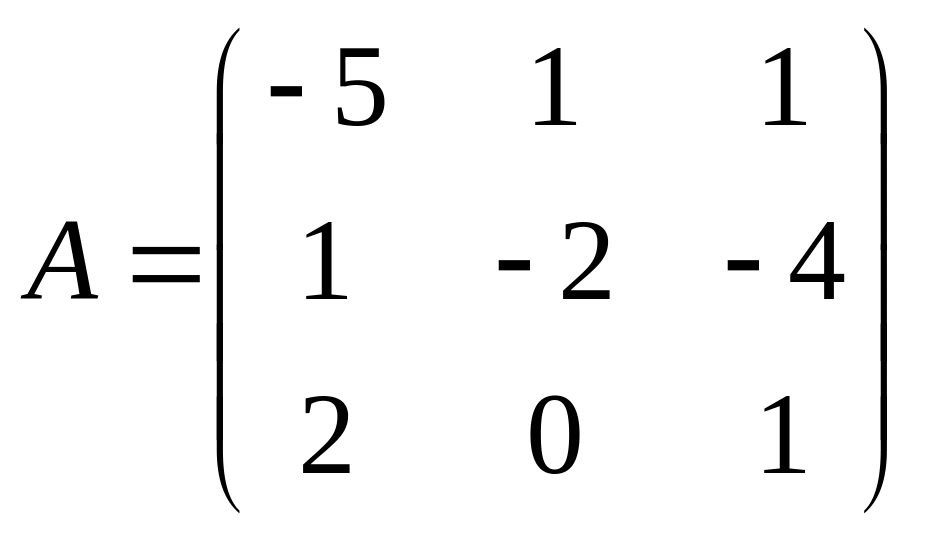 .
.
36. 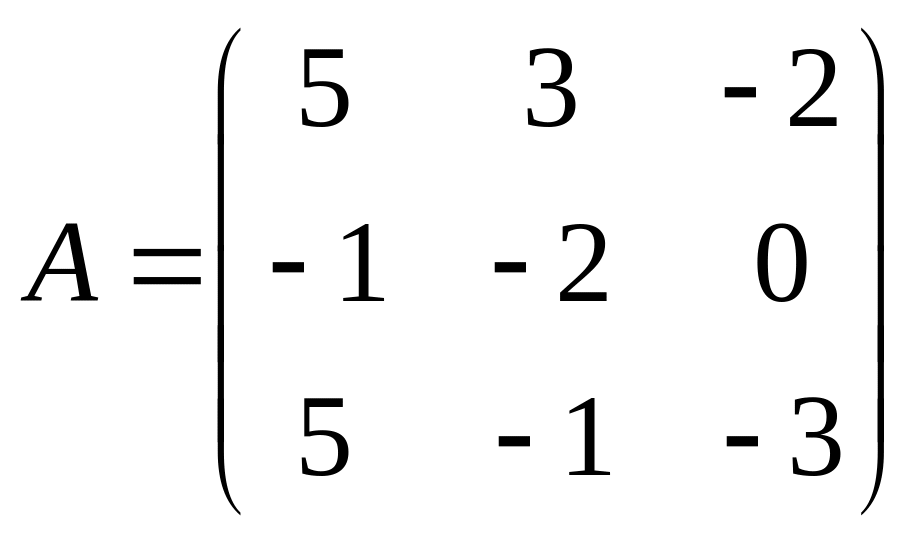 . 37.
. 37. 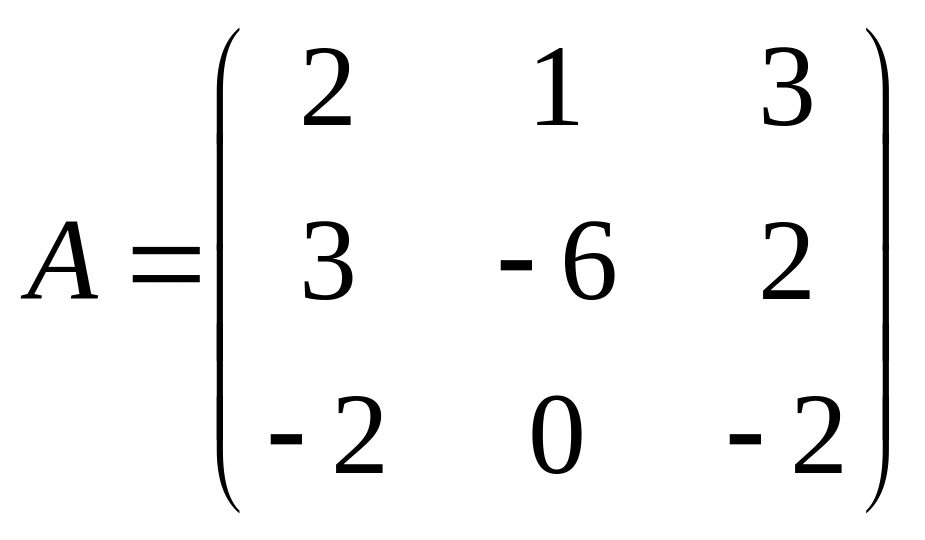 . 38.
. 38. 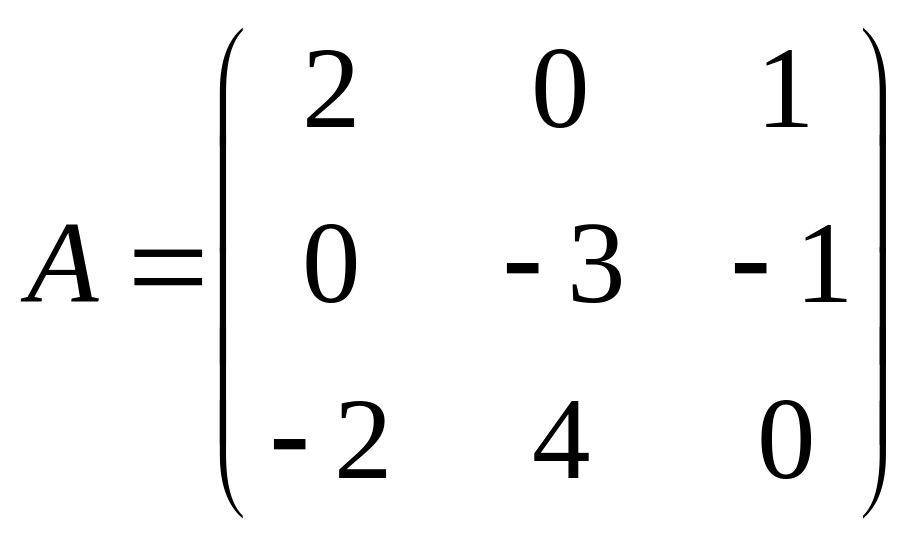 .
.
39. 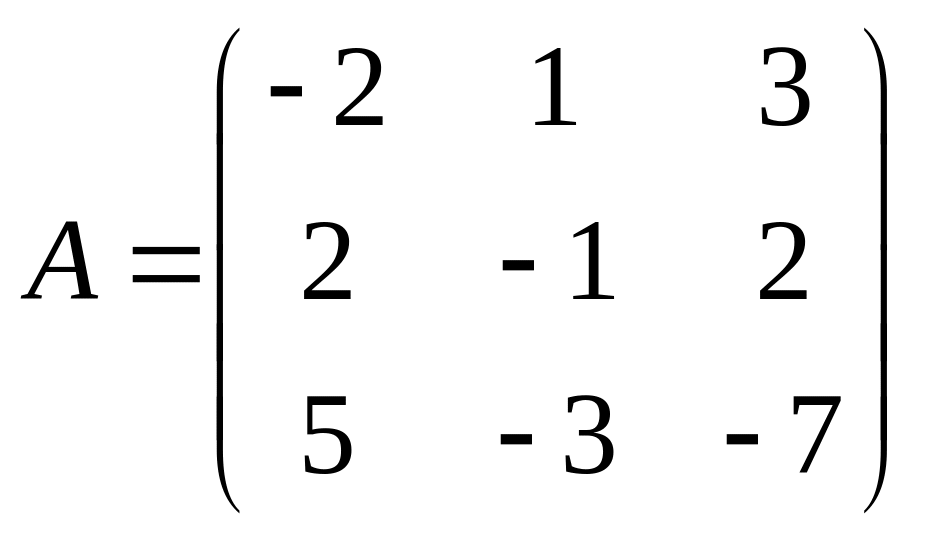 . 40.
. 40.  .
.
В задачах 41 – 60 решить системы линейных уравнений с тремя неизвестными.
41. 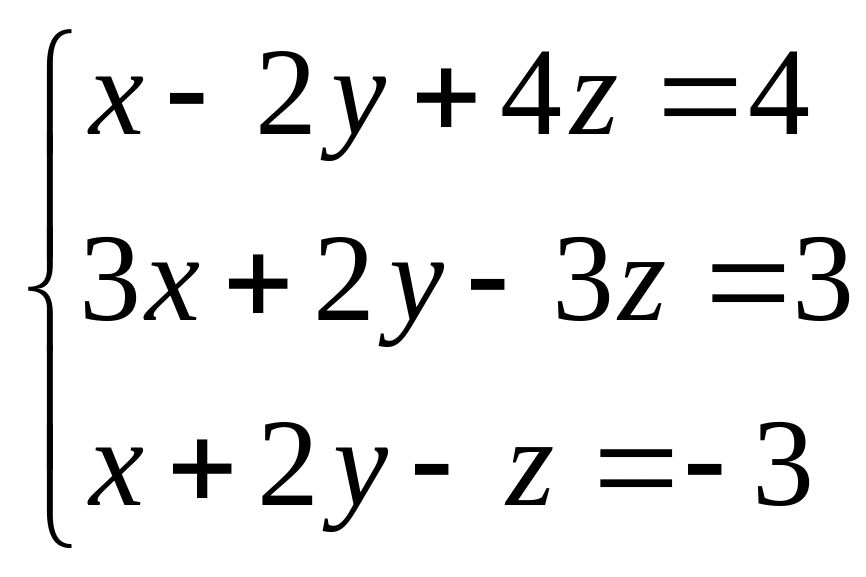 . 42.
. 42.  . 43.
. 43. 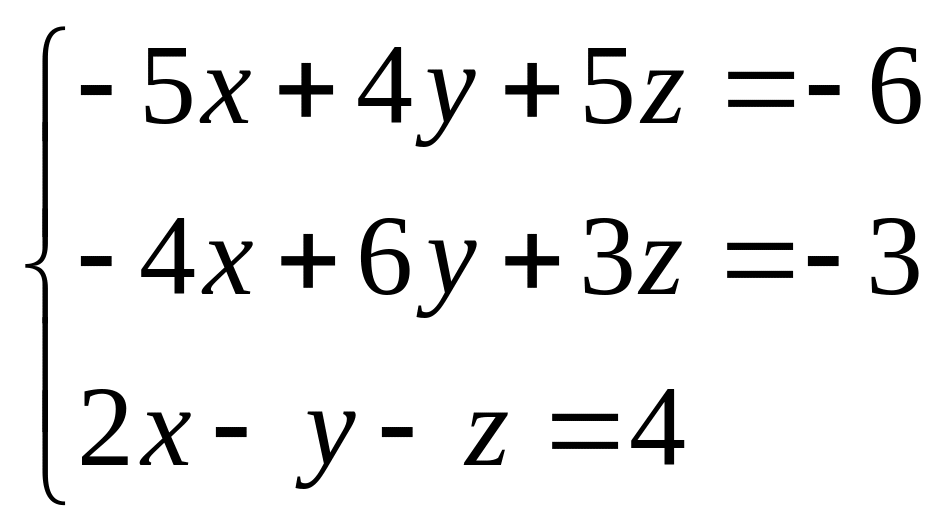 .
.
44.  . 45.
. 45. 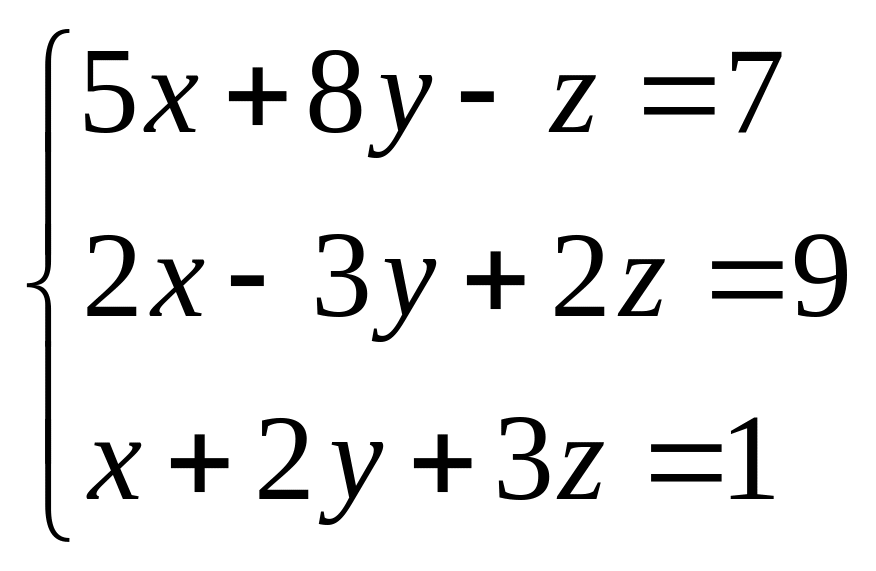 . 46.
. 46. 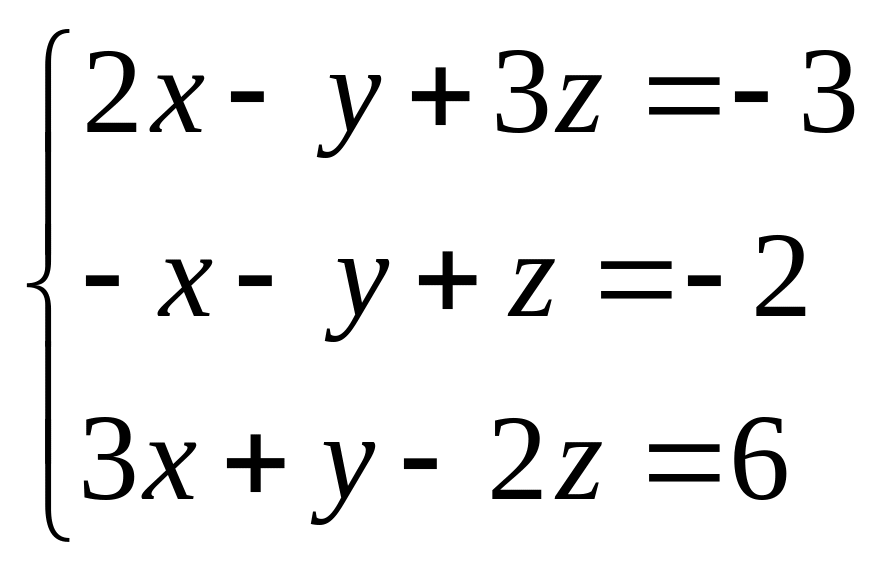 .
.
47. 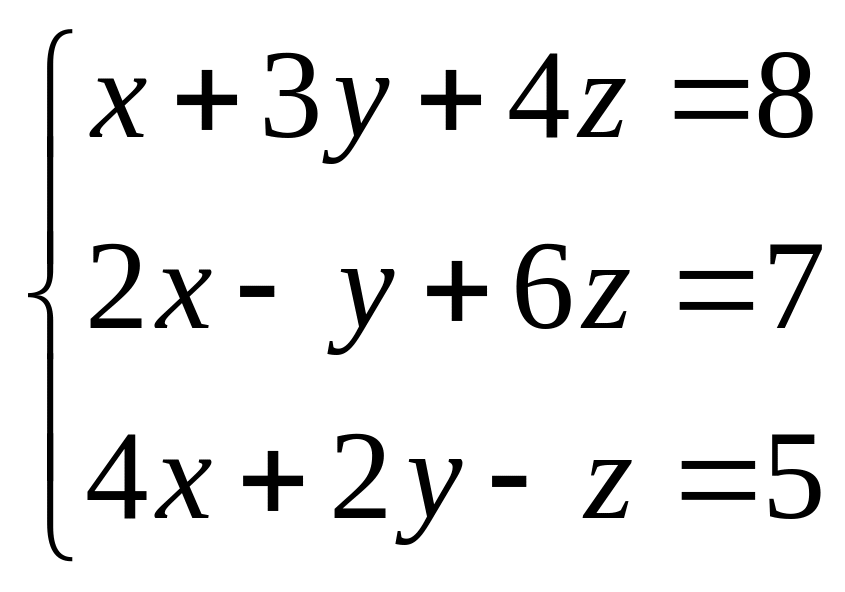 . 48.
. 48. 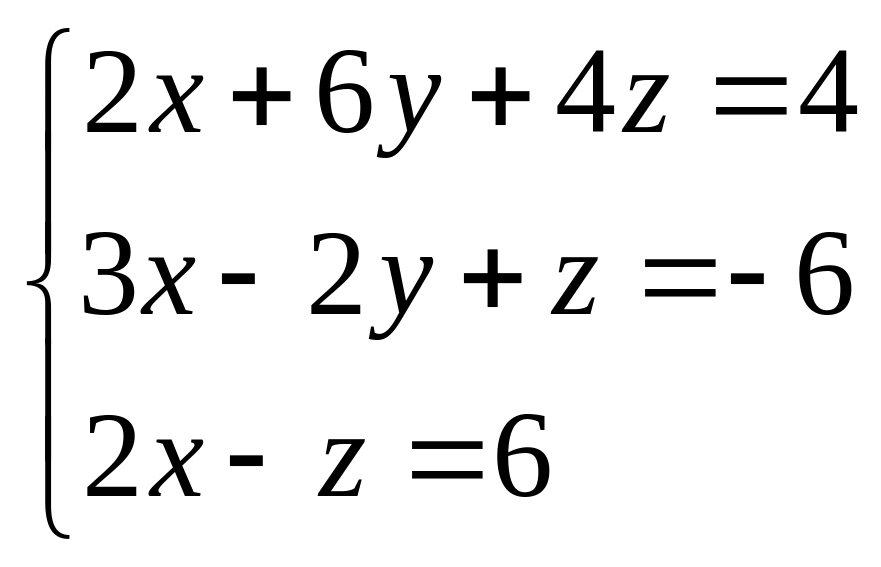 . 49.
. 49. 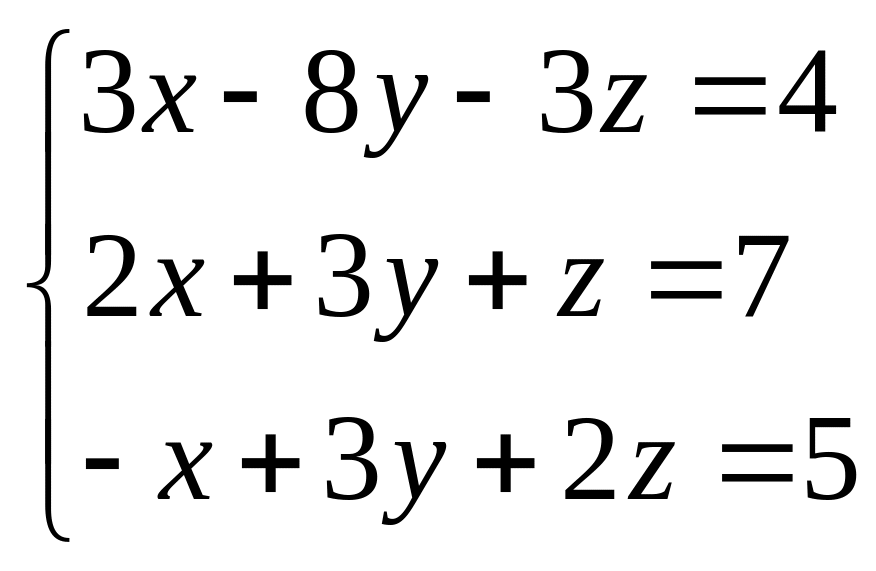 .
.
50. 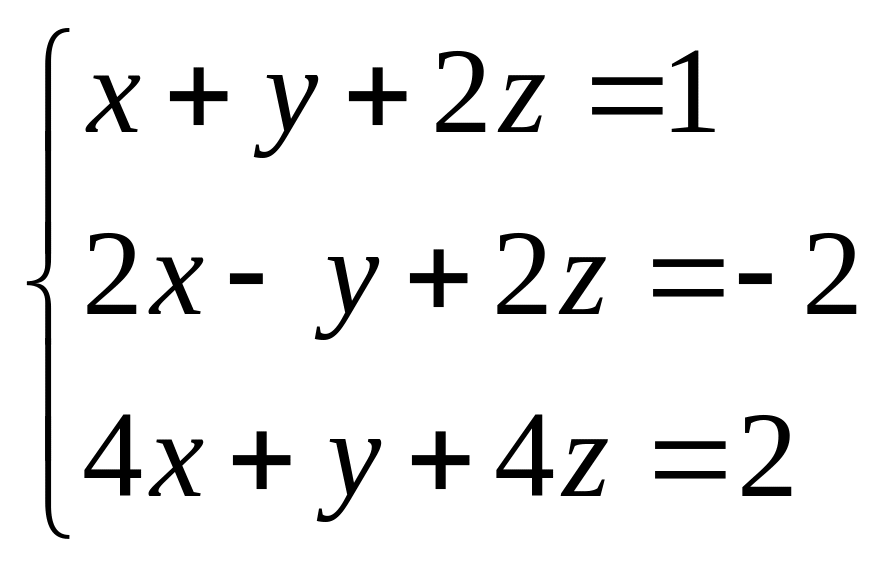 . 51.
. 51. 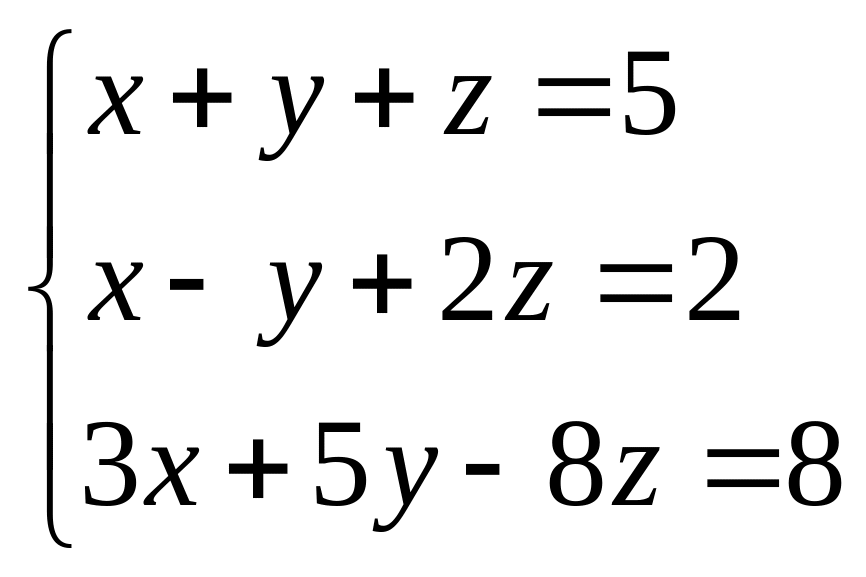 . 52.
. 52. 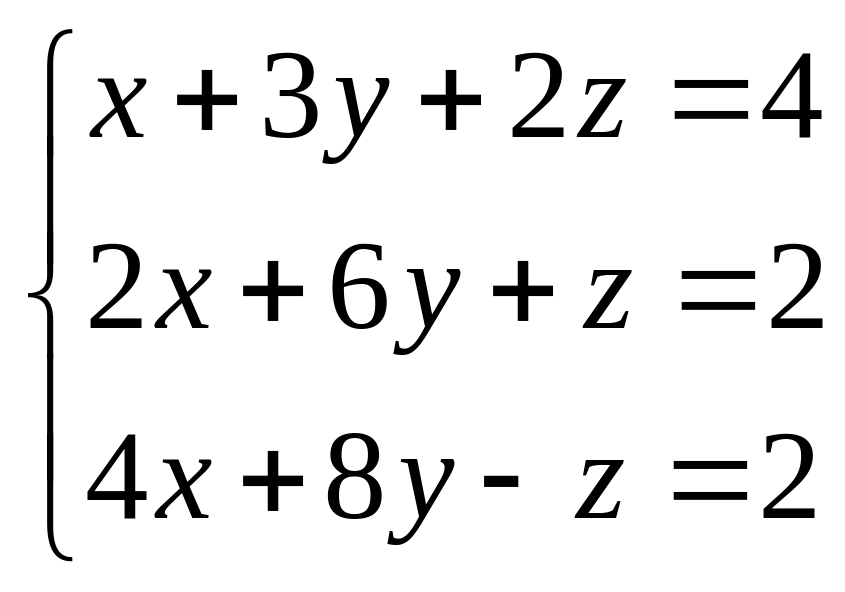 .
.
53.  . 54.
. 54. 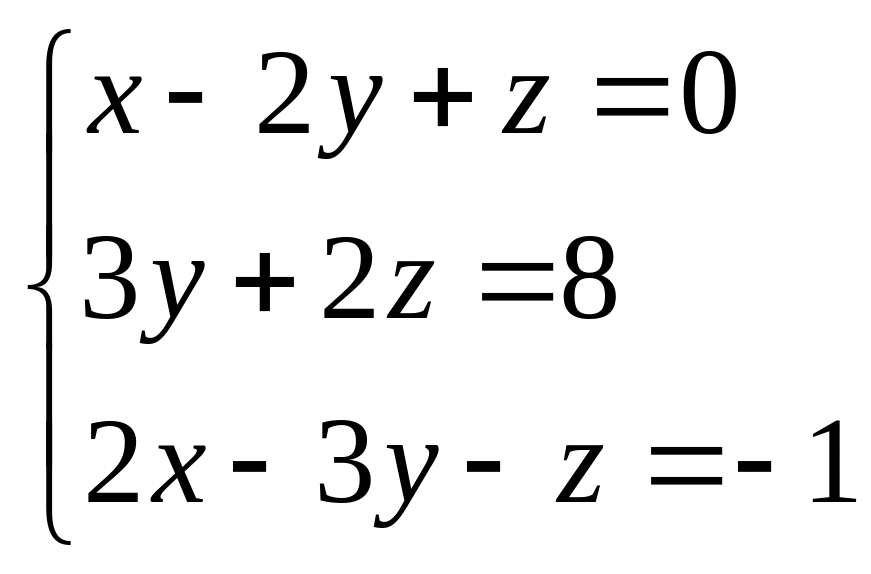 . 55.
. 55.  .
.
56. 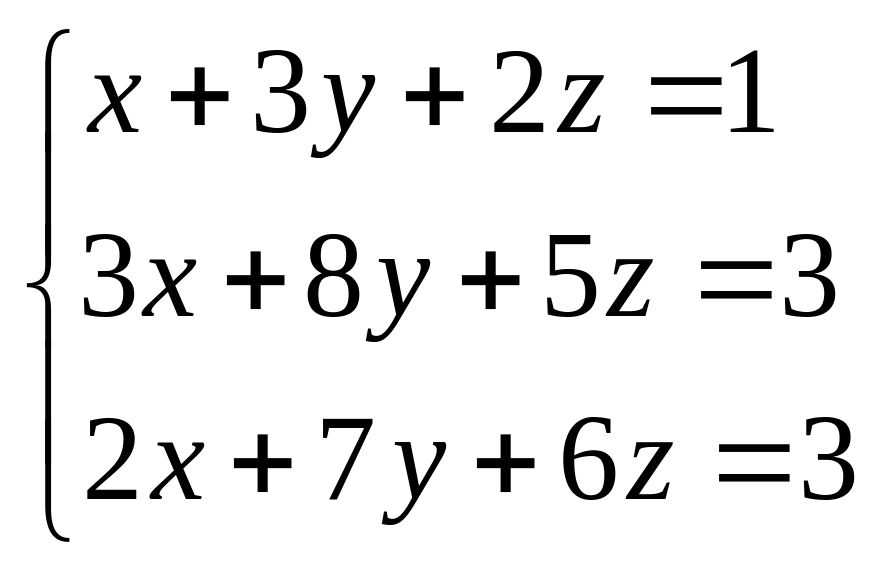 . 57.
. 57. 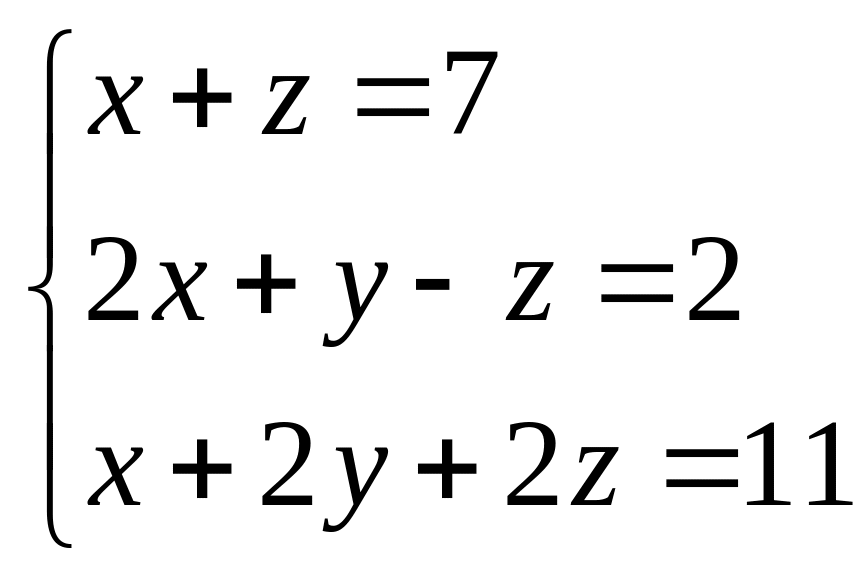 . 58.
. 58. 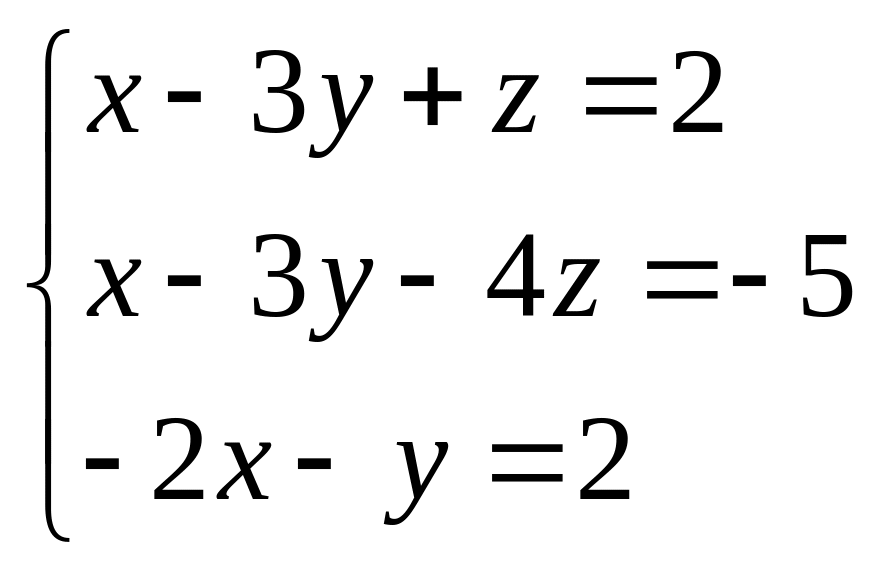 .
.
59. 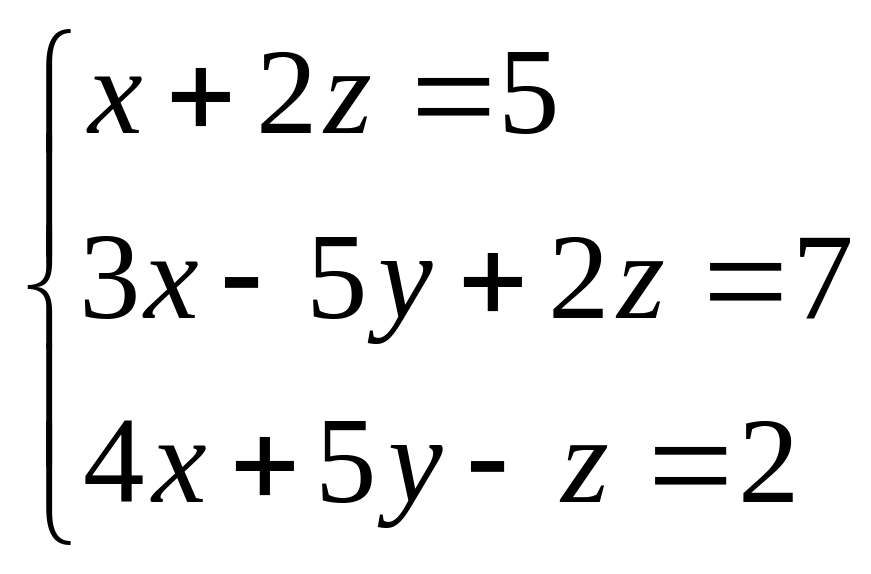 . 60.
. 60.  .
.
В
задачах 61 –
80 построить
треугольник, вершины которого находятся
в точках
![]() ,
,
![]() ,
,
![]() .
Найти:
.
Найти:
1. уравнения
сторон треугольника
![]() ;
;
2. координаты точки пересечения медиан;
3. длину и уравнение высоты, опущенной из вершины ;
4. площадь треугольника.
61. ![]() ,
,
![]() ,
,
![]() . 62.
. 62. ![]() ,
,
![]() ,
,
![]() .
.
63.
,
![]() ,
,
![]() . 64.
. 64. ![]() ,
,
![]() ,
,
![]() .
.
65. ![]() ,
,
![]() ,
,
![]() . 66.
. 66. ![]() ,
,
![]() ,
,
![]() .
.
67. ![]() ,
,
![]() ,
,
![]() . 68.
. 68. ![]() ,
,
![]() ,
.
,
.
69. ![]() ,
,
![]() ,
,
![]() . 70.
. 70. ![]() ,
,
![]() ,
,
![]() .
.
71. ![]() ,
,
![]() ,
,
![]() . 72.
. 72. ![]() ,
,
,
,
![]() .
.
73. ![]() ,
,
![]() ,
,
![]() . 74.
. 74. ![]() ,
,
![]() ,
,
![]() .
.
75.
,
,
![]() . 76.
,
. 76.
,
![]() ,
,
![]() .
.
77. ![]() ,
,
,
,
![]() . 78.
. 78. ![]() ,
,
![]() ,
,
![]() .
.
79. ![]() ,
,
,
,
![]() . 80.
. 80. ![]() ,
,
![]() ,
,
![]() .
.
В
задачах 81 –
100 даны
координаты точек
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Найти:
.
Найти:
1. найти
длину ребра
![]() ;
;
2. уравнение
плоскости, проходящей через точки
,
![]() и
и
![]() ;
;
3. уравнение
высоты опущенной из точки
![]() на плоскость
на плоскость
![]() ;
;
4. площадь грани ;
5. объем
пирамиды
![]() .
.
81. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
82. ![]() ,
,
![]() ,
,
![]() ,
,
![]()
83. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
84. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
85. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
86. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
87. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
88. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
89. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
90. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
91. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
92. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
93. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
94. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
95. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
96. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
97. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
98. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
99. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
100. ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Контрольная работа № 2 «Производная и дифференциал»
В задачах 101 – 120 найти указанные пределы.
101. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
102. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
103. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
104. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
105. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
106. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
107. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
108. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
109. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
110. а) ![]() б)
б) ![]() ; в)
; в) ![]() .
.
111. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
112. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
113. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
114. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
115. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
116. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
117. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
118. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
119. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
120. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
В задачах 121 – 140 для каждой из заданных функций найти точки разрыва и исследовать их характер.
121. ![]() 122.
122. 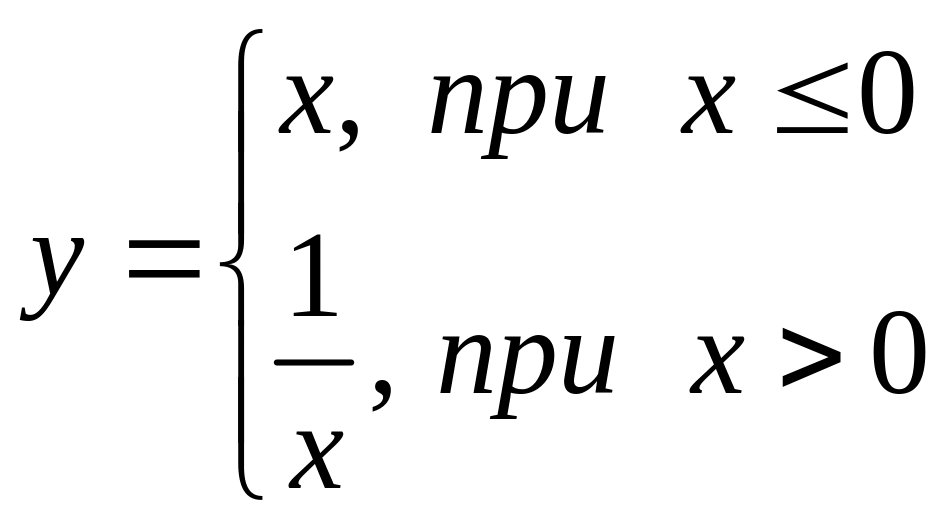 . 123.
. 123. ![]() .
.
124. ![]() . 125.
. 125. 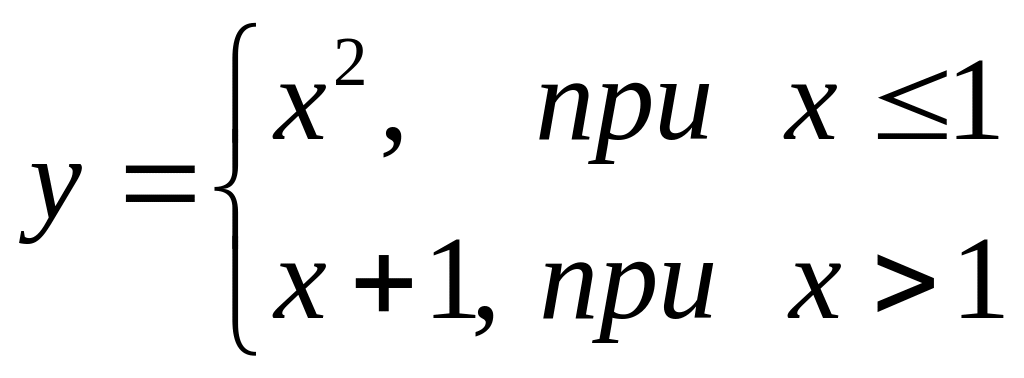 . 126.
. 126. ![]() .
.
127. ![]() . 128.
. 128.  . 129.
. 129. ![]() .
.
130. ![]() . 131.
. 131. 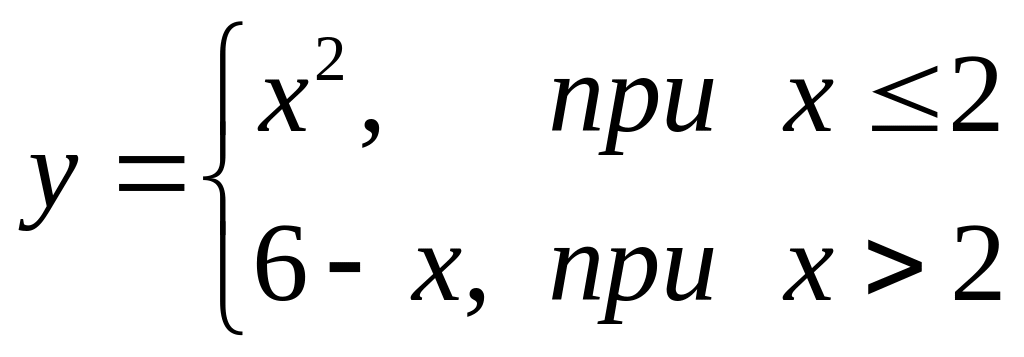 . 132.
. 132. ![]() .
.
133. ![]() . 134.
. 134. 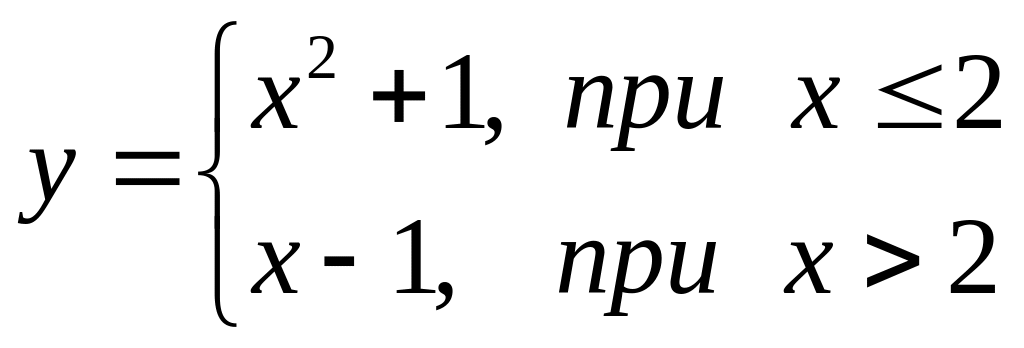 . 135.
. 135. ![]() .
.
136. ![]() . 137.
. 137. 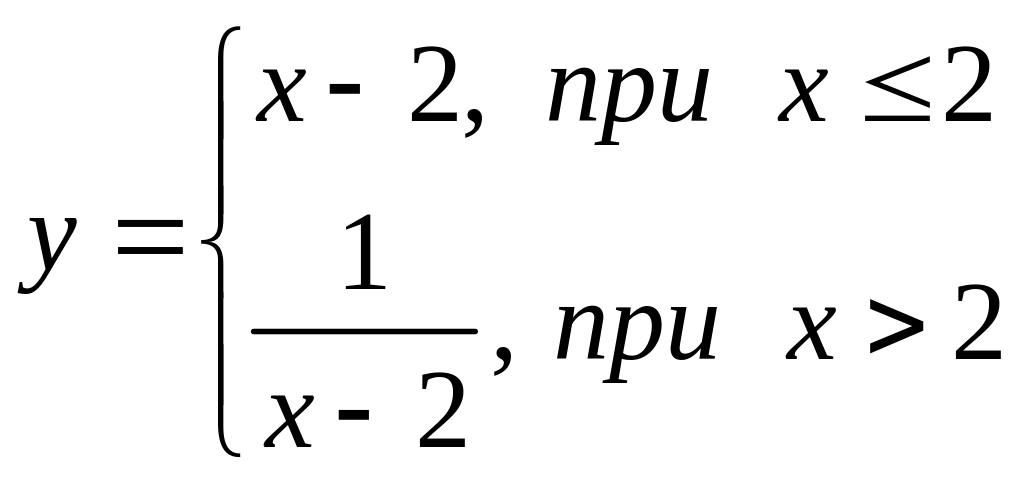 . 138.
. 138. ![]() .
.
139. ![]() 140.
140. 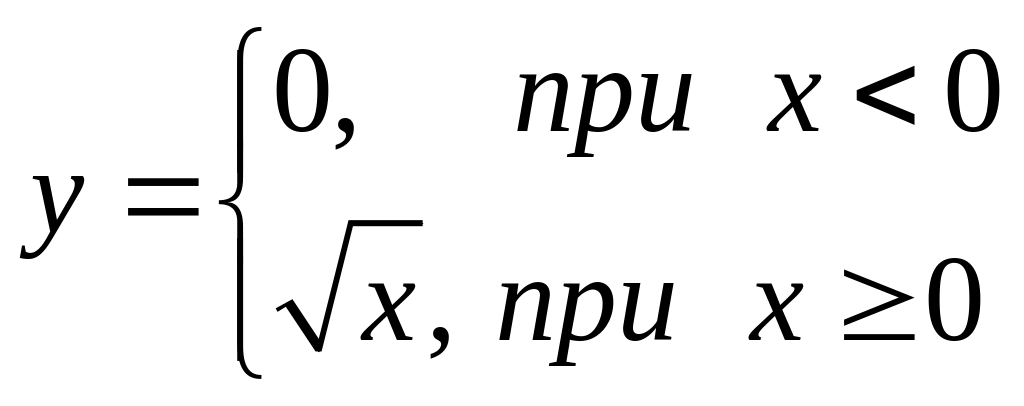 .
.
В задачах 141 – 160 найти производные заданных функций.
141. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
142. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
143. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
144. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
145. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
146. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
147. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
148. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
149. а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() .
.
150. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
151. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
152. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
153. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
154. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
155. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
156. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
157. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
158. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
159. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
160. а) ![]() ; б)
; б) ![]() ; в)
; в)  .
.
В задачах 161 – 180 найти дифференциалы второго порядка.
161. ![]() . 162.
. 162. ![]() . 163.
. 163. ![]() .
.
164. ![]() . 165.
. 165. ![]() . 166.
. 166. ![]() .
.
167.
. 168. ![]() . 169.
. 169. ![]() .
.
170. ![]() . 171.
. 171. ![]() . 172.
. 172. ![]() .
.
173. ![]() . 174.
. 174. ![]() . 175.
. 175. ![]() .
.
176. ![]() . 177.
. 177. ![]() . 178.
. 178. ![]() .
.
179. ![]() . 180.
.
. 180.
.
В задачах 181 – 200 исследовать данные функции методами дифференциального исчисления и построить их графики.
181. 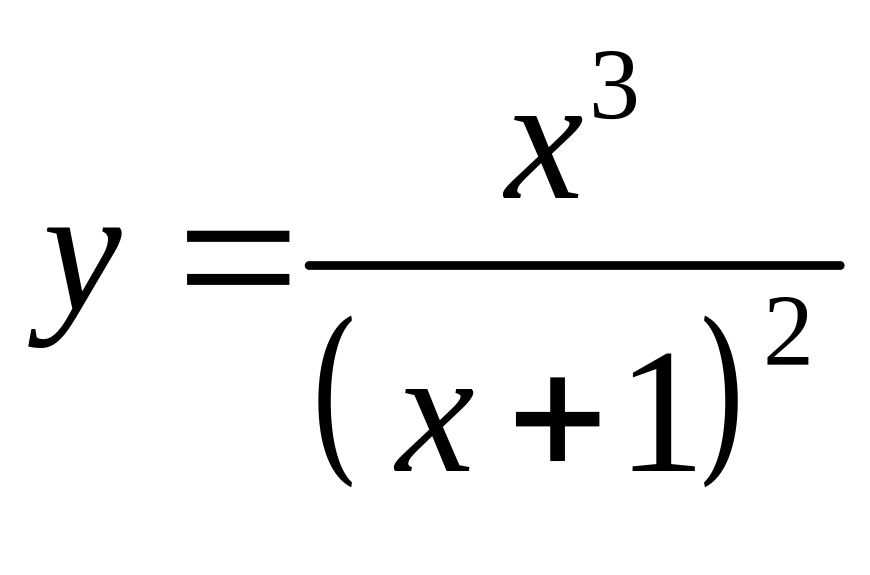 . 182.
. 182. ![]() . 183.
. 183. ![]() .
.
184. ![]() . 185.
. 185. ![]() . 186.
. 186. ![]()
187. ![]() . 188.
. 188. ![]() . 189.
. 189. ![]() .
.
190. ![]() . 191.
. 191. ![]() . 192.
. 192. ![]() .
.
193. ![]() . 194.
. 194. ![]() . 195.
. 195. ![]() .
.
196. ![]() . 197.
. 197. ![]() . 198.
. 198. ![]() .
.
199. ![]() . 200.
. 200. ![]() .
.
