Лабораторная работа № 5 / Лабораторная работа 5

Лабораторная работа № 5

ИССЛЕДОВАНИЕ ПРИНЦИПОВ ОРГАНИЗАЦИИ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА В МВС С ТОПОЛОГИЕЙ ГИПЕРКУБА

Цель работы: изучение способов организации вычислительного процесса в МВС с топологией гиперкуба; сравнение полученных характеристик с аналогичными характеристиками для МВС с распределенной памятью, исследованной в лабораторной работе №4.

В данной работе исследуется МВС, в которой процессоры (вычислительные модули) располагаются в вершинах гиперкуба. На рисунке приведены гиперкубы размерности 3 и 4.

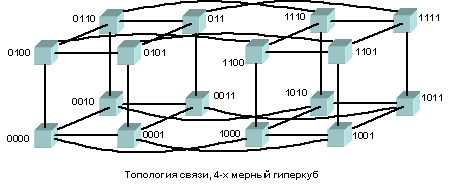
Гиперкуб, состоящий из одной вершины, будем считать гиперкубом нулевой размерности (0-мерный). Две вершины, соединенные ребром образуют 1-мерный гиперкуб. Соединив попарно вершины двух 1-мерных гиперкубов, получим двумерный гиперкуб. Аналогично, соединив два n-мерных гиперкуба, получим (n+1)- мерный гиперкуб. Очевидно, что увеличение на 1 размерности гиперкуба, увеличивает число вершин в два раза. Такая топология обладает рядом достоинств. Между любыми двумя вершинами существует путь длины не более, чем размерность гиперкуба. Так, в МВС с такой топологией из 4096 процессоров (12-мерный гиперкуб) самый длинный путь имеет длину 12. Кроме того, при занятости линии коммутации между двумя вершинами всегда есть альтернативный путь, что делает МВС с такой архитектурой достаточно гибкой.

Домашняя подготовка

Изучить соответствующий раздел лекционного курса и настоящее описание лабораторных работ.

Лабораторное задание

1. Получить у преподавателя исходные данные для исследования – граф задачи из папки Варианты графов для лаб_5.

2. Промоделировать граф, выбранный в соответствии с вариантом с использованием программы Csmodel.exe.

3. Проанализировать временные диаграммы решения задачи в МВС с топологией гиперкуба.

4. Построить зависимости времени решения задачи и ускорения от размерности гиперкуба при различных стратегиях назначения узлов и разных способах передачи данных.

5. Проанализировать полученные результаты. Выбрать конфигурацию системы со средней загруженностью процессоров.

6. Промоделировать решение этой же задачи на МВС с распределенной памятью с аналогичными характеристиками. Проанализировать и объяснить полученные результаты.

Отчет должен содержать:

1. Граф решаемой задачи.

2. Пример временной диаграммы решения задачи.

3. Таблицы результатов и графики, полученных в процессе моделирования.

4. Результаты сравнения систем: МВС с топологией гиперкуба и МВС с распределенной памятью.

Контрольные вопросы

1. Определить число узлов в архитектуре n – мерный гиперкуб и максимальное расстояние между двумя узлами.

2. Перечислить основные свойства архитектуры МВС с топологией типа n – мерный гиперкуб.

3. Какие способы передачи информации существуют в МВС с топологией гиперкуба?

4. Чем объясняется изменение времени решения различных классов задач на МВС с топологией гиперкуба по сравнению с МВС с распределенной памятью?