Упражнение

1.9.4. Используя теорему умножения (см. (3.1.6)) и формулу полной вероятности (1.9.1), докажите формулу Байеса.

Замечание

Вероятности гипотез обычно называют априорными (известными «до опыта»), а вероятности - апостериорными (полученными «после опыта» с появлением события ). Поскольку появление события обычно несёт дополнительную информацию о возможности появления гипотез , апостериорные вероятности являются, как правило, более точными характеристиками этих гипотез, чем априорные вероятности .

Только в случае, когда все условные вероятности равны друг другу, т.е. , , формула (1.9.3) даёт: , , т.е. информация о появлении события не представляет интереса при уточнении априорных вероятностей гипотез.

Пример 1.9.3.

В электронном устройстве, состоящем из двух блоков, возникла неисправность. Предварительный анализ возможных её причин привёл к такой оценке возможностей локализации неисправности: вероятности отказов в первом и втором блоках равны 0,4 и 0,6 соответственно (возможность отказов в обоих блоках исключается). Для уточнения причины неисправности на вход устройства был подан тестовый сигнал, который не проходит на выход с вероятностью 0,2, если неисправен первый блок, и с вероятностью 0,9 при неисправности во втором блоке. Сигнал на выходе не появился. Найти вероятности причин неисправности устройства.

◄Введём обозначения событий: {сигнал на выходе не появился}, {неисправен первый блок}, {неисправен второй блок}.

По условию задачи , , , .

По формуле Байеса находим: , .

Итак, априорные вероятности причин неисправности и близки друг к другу, а апостериорные вероятности и позволяют с большой уверенностью считать, что причина неисправности находится во втором блоке.►

Контрольные вопросы

1. Что называется полной группой попарно несовместных событий?

2. Запишите формулу полной вероятности.

3. Запишите формулу Байеса.

4. В каком случае при расчётах по формулам полной вероятности и Байеса можно использовать неполную группу гипотез?

Задание для самостоятельной работы

1. Решите задачи: [1], №№ 18.242 – 18.244, 18.246, 18.247, 18.251 –18.254, 18.255.

1.10. Вероятности сложных событий

Сложным событием будем называть случайное событие, которое выражено через другие события, происходящие в том же случайном опыте.

Пример 1.10.1.

◄Рассмотрим прохождение сигнала в схеме, составленной из четырёх элементов, см рис. 1.10.1.

2

1 4

3

Рис. 1.10.1. К примеру 1.10.1.

Если элемент схемы исправен, то он пропускает сигнал, в противном случае не пропускает. Обозначим события: {сигнал прошёл от входа до выхода схемы}, { -й элемент исправен}, . Тогда (убедитесь!)

,

т.е. - сложное событие.►

Перечислим основные формулы, используемые при расчётах вероятностей сложных событий.

Вероятность суммы событий:

А) для двух событий

;

б) в частности, если события и несовместны то

;

в) для трёх событий

;

г) для событий

.

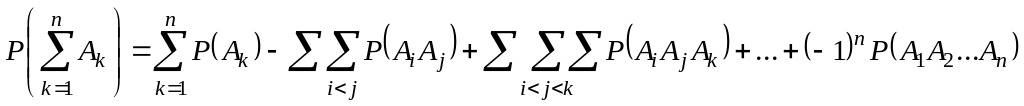д) в частности, если события , попарно несовместны, то

;

е) если же события , независимы в совокупности, то

. (1.10.1)

Вероятность произведения событий:

а) для двух событий

;

б) в частности, если события и независимы, то

.

г) для событий

.

д) в частности, если события , независимы в совокупности, то

. (1.10.2)

Формулы полной вероятности и Байеса:

а) ;

б) .

Формула Бернулли:

вероятность появления ровно успехов в серии из испытаний по схеме Бернулли с вероятностью успеха равна

, где .

Пример 1.10.2.

Убедимся в справедливости равенства (1.10.1).

◄Используя правило де Моргана (1.2.5) с учётом (1.10.2) имеем:

.►

Пример 1.10.3.

Вероятность безотказной работы в течение времени -го элемента в схеме примера 1.10.1. равна , . Отказы элементов являются независимыми в совокупности событиями. Найти вероятность прохождения сигнала на выход схемы в течение этого времени.

◄События {сигнал проходит на выход схемы в течение времени }, { -й элемент исправен течение времени }, связаны соотношением , см пример 1.10.1. Очевидно, . В силу независимости отказов имеем: , .

Окончательно, .►

Контрольные вопросы

1. Что называется сложным событием?

2. Запишите формулы вероятности суммы событий.

3. Запишите формулы вероятности произведения событий.

4. Запишите формулы полной вероятности и Байеса.

5. Запишите формулу Бернулли.

Задание для самостоятельной работы

1. Решите задачи: [1], №№ 18.187, 18.190 – 18.192, 18.196 - 18.203, 18.208 –18.212, 18.219, 18.222 – 18.224.

2. Ознакомьтесь с теоретическим материалом: [2], с. 17 – 22.