1.6. Схема Бернулли

Многие математические модели случайных явлений связаны со случайным опытом, который называется «схемой Бернулли».

Повторные испытания – это последовательное проведение раз одного и того же опыта или одновременное проведение одинаковых опытов.

Схемой Бернулли называют случайный опыт, состоящий в повторных испытаниях, удовлетворяющих следующим условиям:

1) в каждом испытании различают только два исхода: появление определённого события (его называют «успехом») или противоположного события («неудачи»);

2) испытания являются независимыими, т.е. вероятность успеха в каждом испытании не зависит от исходов в других испытаниях;

3) вероятность успеха во всех испытаниях одна и та же: (соответственно, ).

Пример 1.6.1.

Следующие случайные опыты с той или иной степенью приближения вписываются в рамки модели испытаний по схеме Бернулли:

1. Последовательное подбрасывание правильной монеты раз и наблюдение выпадающих сторон монеты. Успехом можно считать событие {выпал герб}, вероятность успеха .

2. Одновременное подбрасывание игральных костей. Успехом считаем, например, событие {выпало 6 очков}, вероятность успеха .

3. Последовательность выстрелов стрелка' по мишени. Успех - {попадание в мишень}. Этот опыт лишь приближённо можно назвать схемой Бернулли, т.к. вероятность успеха может изменяться от испытания к испытанию из-за «пристрелки» или утомления стрелка'.

4. Проверка исправности изделий, произведённых в одинаковых условиях. Успех - {изделие исправно}.

5. Опыт состоит в наблюдении радиоактивного распада определённого количества радиоактивного изотопа. Зная массу радиоактивного вещества, можно определить число содержащихся в нём атомов и, наблюдая распад в течение заданного промежутка времени длительности , рассматривать опыт как последовательность испытаний по схеме Бернулли, считая успехом в -ом «испытании» событие {распад ядра -го атома в течение промежутка времени }.

Пример 1.6.2.

Опишем пространство элементарных исходов случайного опыта – схемы Бернулли.

◄Элементарными исходами серии из испытаний является всевозможные последовательности длины , состоящие из событий и , различающиеся составом (т.е. числом событий и числом событий , ) и порядком следования и . Например, при элементарными исходами будут: , , , и т. п.

Число элементарных исходов равно числу размещений из двух элементов ( и ) по с повторениями, см. (1.2.7), т.е. .►

Упражнения

1.6.1. Для схемы Бернулли при :

а) перечислите все элементарные исходы;

б) найдите количества элементарных исходов, составляющих события {появилось ровно успехов}, .

Пример 1.6.3.

Найдём вероятность того, что в испытаниях по схеме Бернулли с вероятностью успеха произойдёт ровно успехов.

◄Событие {в испытаниях появилось ровно успехов} происходит тогда и только тогда, когда реализуется какой-либо из элементарных исходов (последовательностей событий и ), содержащих событий и событий . Вероятность любого такого исхода в силу независимости испытаний Бернулли равна .

Число таких исходов равно числу способов выбора мест для событий из общего числа мест в последовательности событий и (на остальных местах будут стоять события ). Поэтому число элементарных исходов, составляющих событие , равно см. (1.2.3). Окончательно,

(1.6.1)

Равенство (1.6.1) называют формулой Бернулли.►

Упражнения

1.6.2. Для испытаний по схеме Бернулли найти вероятности событий:

а) {не появилось ни одного успеха};

б) {появился хотя бы один успех};

в) {успех появился не менее раз и не более раз}.

1.6.3. Монету подбрасывают 10 раз. Найти вероятность выпадения герба:

а) ровно 5 раз;

б) не более 5 раз;

в) хотя бы один раз.

Пример 1.6.3.

Вероятность выигрыша на один лотерейный билет . Сколько билетов нужно купить, для того, чтобы вероятность хотя бы одного выигрыша была не меньше, чем ?

◄Предположим, что куплено билетов и обозначим число выигрышей через . Используя формулу (1.6.1.), получим:

, откуда . Таким образом, нужно купить не менее 230 билетов.►

Пример 1.6.4.

Найдём рекуррентную формулу для вероятностей и появления ровно и ровно успехов в серии из испытаний по схеме Бернулли с вероятностью успеха .

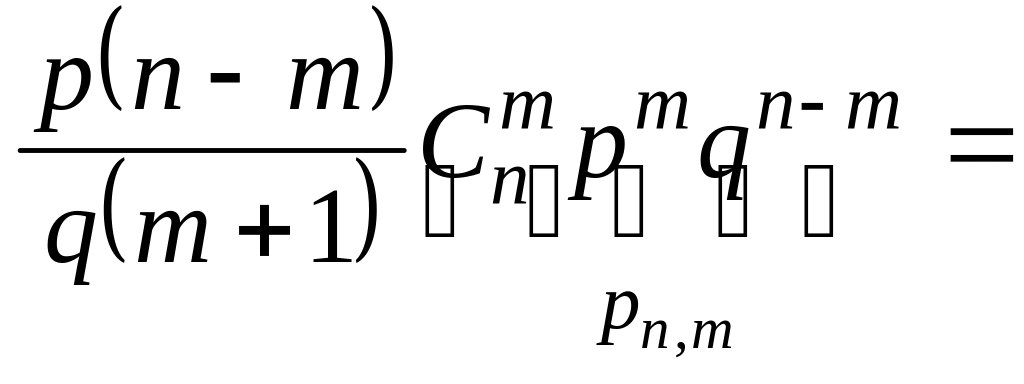
◄С помощью формулы Бернулли (1.6.1) находим: . Итак,

(1.6.2)

- искомая рекуррентная формула.►

Пример 1.6.5.

Пусть - наиболее вероятное число успехов в серии из испытаний по схеме Бернулли с вероятностью успеха . Покажем, что

. (1.6.3)

◄По условию задачи и . Запишем формулу (1.6.2) для и : ,

Запишем формулу (1.6.2) для : . По условию , откуда получаем: или , т.е. . Первое из неравенств (1.6.3) доказано.

Запишем теперь формулу (1.6.2) для : , откуда . По условию , поэтому или , откуда получаем второе неравенство из (1.6.3). ►

Упражнение

1.6.4. Процент брака при изготовлении приборов составляет 5%. Для продажи взяли партию из 200 приборов. Найти наиболее вероятное число бракованных приборов в партии.

Ответы к упражнениям

1.6.1. а) ,

, , , ,

, , , , , ,

, , , ,

б) , , , , .

1.6.2. а) ; б) ; в) .

1.6.3. а) ; б) ; в) .

1.6.4. .

Контрольные вопросы

1. Какой случайный опыт называют схемой Бернулли?

2. Запишите формулу Бернулли для вероятности появления ровно успехов в серии из испытаний.

Задание для самостоятельной работы

Решите задачи: [ ], №№ 18.312 - 18.316, 18.322, 18.325, 18.328.