2.4 Методические указания к решению задач №6

Каналы различного живого сечения будут гидравлически наивыгоднейшими при определенных значениях относительной ширины канала .

Для гидравлически наивыгоднейшего трапецеидального сечения соотношения ширины канала к глубине (β _г.н.) зависят от коэффициента заложения откосов m:

.

(12)

Для прямоугольного сечения (m = 0) 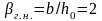, т.е. .

Для решения задачи можно использовать метод подбора (см. задачу №4) или «показательный закон» (см. задачу №5). Предварительно следует рассчитать относительную ширину канала β по формуле (12), тогда ширина канала будет определяться, как .

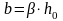2.5 Методические указания к решению задач №7

Канализационные коллекторы относятся к каналам замкнутого поперечного профиля. Эти трубопроводы работают как безнапорные, поэтому с гидравлической точки зрения ничем не отличаются от открытых каналов.

При равномерном движении расчеты ведутся по формуле Шези с учетом особенностей, присущих только руслам замкнутого сечения.

При расчете каналов замкнутого профиля вводится понятие степени наполнения трубы

.

(13)

где h – высота (глубина) слоя воды в трубе, м;

d – полная высота трубы (диаметр), м.

Расход и средняя скорость в каналах замкнутого сечения определяются по формулам

			(14)
				(15)

где 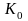и - расходная, м³/с, и скоростная, м/с, характеристики, соответствующие полному заполнению трубы (при а = 1). В таблице (Приложение Б) приведены величины и для круглых труб в зависимости от диаметра.

А и В – коэффициенты.

Величины А и В практически не зависят от размеров рассматриваемой трубы, а зависят только от формы поперечного профиля и от степени наполнения трубы а. Для труб круглого сечения коэффициенты А и В определяются по графику (Приложение В).

2.6 Методические указания к решению задач №8

Для того чтобы определить тип кривой свободной поверхности потока в русле, необходимо знать уклон дна русла i, критический уклон i_кр, глубину равномерного движения h₀, критическую глубину h_кр и глубину потока в расчетном створе h.

Критическая глубина для русел прямоугольного сечения определяется по формуле

.

(16)

Критическим называется уклон, при котором при равномерном движении воды в русле нормальная глубина равна критической (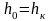 ). Для заданного расхода Q критический уклон определяется по формуле

.

(17)

В открытых призматических руслах при неравномерном движении, в зависимости от уклона дна и условий протекания потока в начале и в конце рассматриваемого участка, может образовываться ряд форм кривых свободной поверхности потока.

Пять возможных случаев кривых свободной поверхности

I случай. Уклон дна меньше критического (i < i_k), при этом h₀ > h_k, (рисунок 3). Неравномерное движение может устанавливаться в трех зонах, и возможны три вида кривых свободной поверхности: 1) в зоне а, при h > h₀, - кривая подпора Iа; 2) в зоне b, при h₀ > h > h_k, - кривая спада Ib; 3) в зоне с, при h < h_к, - кривая подпора Iс.

Рисунок 3 – Кривые свободной поверхности при i < i_k

В зоне а глубина может изменяться от нормальной глубины h₀ до весьма большой (теоретически бесконечно большой). Вначале кривая свободной поверхности асимптотически приближается к линии нормальных глубин, а в конце при больших глубинах стремиться стать горизонтальной.

В зоне b глубина вдоль движения уменьшается от нормальной глубины h₀ до критической глубины h_k.

В зоне c глубина вдоль движения возрастает от какой-то начальной h < h_k до критической глубины.

II случай. Уклон дна больше критического (i > i_k), при этом h₀ < h_k, (рисунок 4). Неравномерное движение может устанавливаться в трех зонах, и возможны три вида кривых свободной поверхности: 1) в зоне а, при h > h_к, - кривая подпора IIа, которая подходит под крутым углом к линии критических глубин и стремится стать горизонтальной при больших глубинах; 2) в зоне b, при h_k > h > h₀, - кривая спада IIb, глубины уменьшаются от h_к, асимптотически приближаясь к значению нормальной глубины h₀; 3) в зоне с, при h < h₀, - кривая подпора IIс, глубины возрастают вдоль движения, асимптотически приближаясь к значению нормальной глубины h₀.

.

Рисунок 4 - Кривые свободной поверхности при i > i_k

III случай. Уклон дна равен критическому (i = i_k), h₀ = h_k, (рисунок 5). Неравномерное движение может происходить в двух зонах а и с. В зоне а устанавливается кривая подпора типа IIIa, а в зоне с кривая подпора типа IIIс. Кривые подпора IIIa и IIIc по своей форме близки к горизонтальным прямым.

Рисунок 5 – Кривые свободной поверхности при i = i_k

IV случай. Уклон дна русла i = 0. В горизонтальном канале не может быть равномерного движения и, следовательно, нормальной глубины. Поэтому неравномерное движение может быть только в двух зонах b и с (рисунок 6).

Рисунок 6 – Кривые свободной поверхности при i = 0

В зоне b, при h > h_к, устанавливается кривая спада типа IVb. В зоне с, при h < h_к, устанавливается кривая подпора типа IVc.

V случай. Русло имеет обратный уклон (i < 0). Как и в предыдущем случае, здесь не может быть нормальной глубины и неравномерное движение рассматривается в двух зонах b и с (рисунок 7).

Рисунок 7 – Кривые свободной поверхности при i < 0

В зоне b, при h > h_к, устанавливается кривая спада типа Vb. В зоне с, при h < h_к, устанавливается кривая подпора типа Vc.

Для расчета кривой свободной поверхности используем метод конечных разностей В.И. Чарномского.

Расстояние l между сечениями определяется по формуле

,

(18)

где Э₁ и Э₂ – удельные энергии соответствующих сечений, м;

,

(19)

i – уклон дна русла;

- средний уклон трения на участке.

Для получения большей точности расчета кривую свободной поверхности следует разбить на несколько участков. Чем больше будет расчетных участков, тем выше получится точность расчетов.

Порядок расчета по методу В.И. Чарномского:

• определяется критическая глубина и критический уклон (по формулам 16, 17);

• устанавливается форма кривой свободной поверхности потока (см. рисунки 3 – 7);

• определяется нормальная глубина потока h₀;

• расчет кривой свободной поверхности ведется в интервале глубин от h₀ до h_p (где h_p – глубина в расчетном сечении по варианту);

• кривая свободной поверхности разбивается на отдельные участки с глубинами в сечениях h₂, h₃, …, в интервале от h₁ = h_нач до h_n = h_кон;

• определяется удельная энергия сечений в начале и конце каждого участка по формуле (19);

• для каждого сечения определяется уклон трения

,

(20)

а затем его средняя величина для участка

;

(21)

• производится расчет длины каждого участка (l_1-2, l_2-3,…, l_{(n-1) – n}) по формуле (18). Все расчеты следует выполнять в табличной форме (см. таблица 12, таблица 13).

Таблица 12

Параметры	Глубины в сечении, м
	h1	h2	…	…	hn

Таблица 13

Параметры	Интервалы между сечениями
	h1- h2	h2- h3	…..	hn-1- hn

• определяется суммарная длина кривой свободной поверхности.
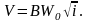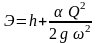