2 Методические указания к решению задач

2.1 Методические указания к решению задач №1-3

При расчете каналов на равномерное движение используется формула Шези:

,

(1)

где V – средняя скорость движения воды в канале, м/с;

С – коэффициент Шези, м^0,5/с;

R – гидравлический радиус, м;

I - пьезометрический уклон, при равномерном движении равен уклону дна канала (i), м/м.

Расход воды в канале Q, м³/с, определяется по формуле

,

(2)

где ω – площадь живого сечения потока в канале, м², для русел трапецеидального сечения определяется по формуле

.

(3)

Для определения параметров, входящих в формулы (1) и (2) используются следующие зависимости:

- коэффициент Шези определяется по формуле Маннинга

(4)

где n – коэффициент шероховатости русла, принимается по приложению А в зависимости от типа крепления стенок канала;

- гидравлический радиус

,

(5)

где χ – смоченный периметр, м, определяется по формулам:

- для канала прямоугольного сечения

,

(6)

- для канала трапецеидального сечения

,

(7)

b – ширина канала по дну, м;

h₀ – нормальная глубина воды в канале, м, (т.е. глубина воды при равномерном движении);

m – коэффициент заложения откосов.

2.2 Методические указания к решению задачи №4

При расчете каналов для определения нормальной глубины используется способ подбора, при котором, задаваясь глубинами h₁, h₂, ..., h_n вычисляют соответствующие значения ω, χ, R и Q. Результаты вычислений сводятся в таблицу 11.

Таблица 11

h, м
h1	ω1	χ1	R1	C1	Q1
h2	ω2	χ2	R2	C2	Q2
…..	…..	…..	…..	…..	…..
hn	ωn	χn	Rn	Cn	Qn

Найденные значения расходов сравниваются с заданным расходом Q. Если 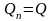, то h_n равна искомой глубине h₀.

Решение задачи можно упростить, построив график зависимости по нескольким произвольным точкам (рисунок 1). По графику определяют искомую глубину h₀, соответствующую заданному значению расхода Q.

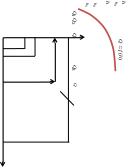
Рисунок 1

2.3 Методические указания к решению задачи №5

Аналитически нормальную глубину можно найти из приближенной зависимости, называемой показательным законом, согласно которому

,

(8)

где x – гидравлический показатель русла;

h₁ и h₂ – произвольно назначенные глубины;

К₁ и К₂ – соответствующие им расходные характеристики, м³/с, определяемые по формуле

.

(9)

Гидравлический показатель русла x определяется из формулы (8)

.

(10)

Вычислив предварительно значение расчетной расходной характеристики , определяется искомая нормальная глубина протекания потока

.

(11)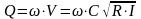
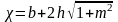
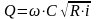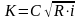