3. Лінійне і квадратичне інтерполювання

Найпростішими випадками інтерполювання многочленом є випадки, коли і .

При маємо многочлен першого степеня , тобто лінійну функцію, тому інтерполювання многочленом називається лінійним інтерполюванням.

Нехай для невідомої функції маємо її значення у двох точках :

, .

Графік лінійної функції повинен проходити через ці точки, тому невідомі коефіцієнти і можна знайти з системи рівнянь:

.

Розв’язавши цю систему одержимо:

,

тоді

,

або

, (*)

відповідно функцію можна представити наближеною рівністю:

,

яка називається формулою лінійного інтерполювання.

Геометричний смисл: заміна дуги кривої на відрізком прямої лінії , що проходить через точки , (рис. 2).

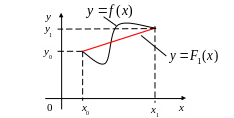
Рис. 2.

Більш точні результати можна одержати, якщо замість лінійної інтерполяції використовувати квадратичну інтерполяцію ( ), тобто якщо дугу кривої заміняти не відрізком прямої лінії, а параболою

.

Нехай для невідомої функції маємо її значення у трьох точках :

, , .

Графік інтерполяційного многочлена повинен проходити через ці точки, тому невідомі коефіцієнти , і можна знайти з системи рівнянь:

.

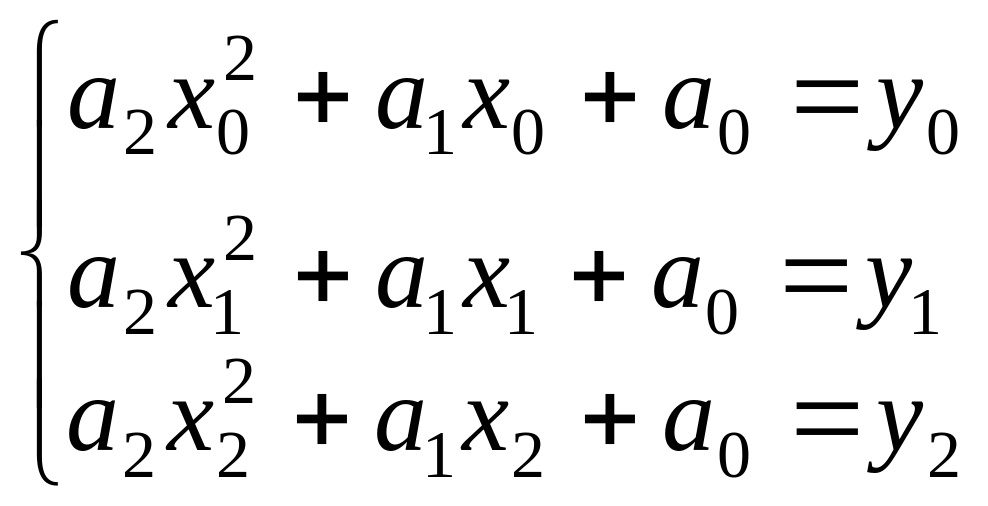Наближене значення функції в будь-якій точці обчислюється за формулою:

(**)

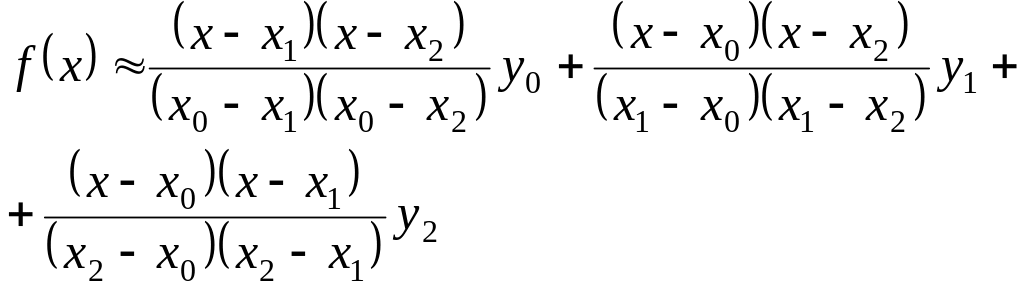Цю формулу називають формулою квадратичного інтерполювання.

Геометричний смисл: заміна дуги кривої на дугою параболи , що проходить через точки , , (рис. 3).

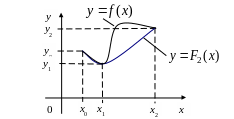
Рис. 3.

4. Параболічне інтерполювання. Інтерполяційна формула Лагранжа

Нехай деяка функція задана своїми значеннями в -му вузлі інтерполювання :

. (1)

В якості інтерполяційного многочлена візьмемо многочлен n-го степеня виду:

, (2)

причому значення у вузлах інтерполювання повинні співпадати зі значеннями заданої функції, тобто: . (3)

Ця умова визначає систему з -го лінійного рівняння виду:

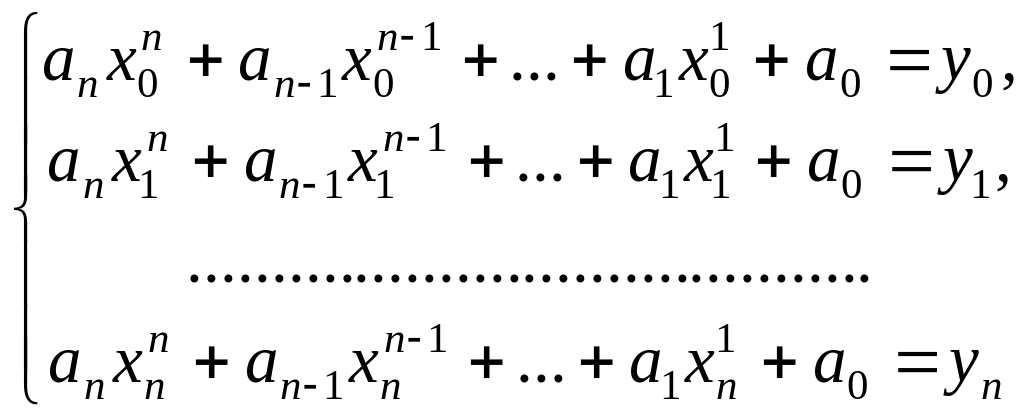(4)

для знаходження коефіцієнта шуканого многочлена .

Оскільки вузли інтерполювання різні ( ), то одержана система лінійних рівнянь має єдиний розв’язок. Отже, інтерполяційний многочлен виду (2) існує і є єдиним, але у залежності від способу побудови форма запису його може бути різною, наприклад у формі Ньютона або Гаусса. Єдиність інтерполяційного мнолочлена виду (2) можна довести методом відсупротивного.

Для побудови многочлена будемо будувати допоміжні многочлени степені .

Многочлен побудуємо так, щоб у вузлі інтерполювання він прийняв значення , а в інших вузлах .

Такий многочлен має вигляд:

.

Дійсно, вузли інтерполювання є коренями многочлена , тому, , а в точці чисельник дорівнює знаменнику, отже, .

Далі будуємо многочлен

.

Зрозуміло, що

, а .

Аналогічним чином можна побудувати многочлени , рівні 1 відповідно у вузлах і рівні нулю в усіх інших вузлах інтерполювання.

У загальному вигляді многочлени можно записать так:

, .

Покажемо далі, що шуканий многочлен має вигляд:

. (5)

Дійсно, добутки перетворюються в нуль у всіх вузлах інтерполювання, крім вузла , де вони рівні , оскільки , тобто

.

Крім того, степінь многочлена рівна , оскільки кожний доданок суми є многочленом степені .

Побудований многочлен (5) називають інтерполяційним многочленом Лагранжа і записують так:

. (6)

Інтерполяційна формула Лагранжа для наближеного обчислення значень функції у проміжних точках має вигляд:

. (7)

У частинному випадку, якщо є два вузли інтерполювання і , то з формули (6) одержуємо формулу лінійного інтерполювання (*), а якщо три вузли , то формулу квадратичного інтерполювання (**).

Оскільки крива, яка є графіком многочлена , називається параболою -го порядку, то інтерполювання многочленом Лагранжа називають параболічним інтерполюванням.

Зрозуміло, що, чим більше вузлів інтерполювання на відрізку , тим точніше інтерполяційний многочлен наближає задану функцію.

Приклад 1. Для функції, значення якої в чотирьох точках задані таблицею побудувати інтерполяційний многочлен Лагранжа:

x	0	1	2	4
f(x)	1	3	2	4

Відповідь: , де a₃=0.541(6) a₂=-3.125 a₁=4.58(3), a₀=1.