
- •122 «Комп’ютерні науки та інформаційні технології»
- •124 «Системний аналіз»
- •Лабораторна робота №1-2
- •І. Теоретичний матеріал
- •4. Числа і числові константи
- •4.1. Системи числення
- •5. Рядкові дані
- •6. Складні типи даних: вектори, матриці, масиви, таблиці, списки
- •7. Оператори, функції і вирази
- •7.1. Оператори та їх пріоритет
- •7.2. Функції та їх класифікація
- •8. Системи комп’ютерної математики в Internet
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •І. Теоретичний матеріал
- •1. Введення матриць
- •2. Матричні оператори
- •3. Матричні функції
- •4. Розв’язування матричних рівнянь
- •5. Символьні матричні перетворення
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •IV. Завдання для самостійного виконання
- •І. Теоретичний матеріал
- •1. Знаходження границь функцій
- •2. Аналітичне і чисельне диференціювання та їх реалізація в системі Mathcad
- •3. Дослідження функцій і побудова їх графіків за допомогою системи Mathcad
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •Лабораторна робота №7-8
- •І. Теоретичний матеріал
- •3. Тривимірна графіка
- •4. Робота з анімаційною графікою
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •Лабораторна робота № 9-10
- •І. Теоретичний матеріал
- •1. Умови iснування розв’язку екстремальної задачі
- •2. Класичний метод знаходження екстремумiв функцiї однiєї змiнної
- •3. Класичний метод знаходження екстремумiв функцiї багатьох змiнних
- •4. Основні засоби пакету Mathcad щодо розв’язування задач оптимізації
- •5. Розв’язування задач математичного програмування в середовищі Mathcad
- •II. Завдання до лабораторної роботи
- •III. Індивідуальні завдання
- •Іv. Контрольні запитання
- •Лабораторна робота № 11-12
- •І. Теоретичний матеріал
- •Іі. Завдання до лабораторної роботи
- •III. Індивідуальні завдання
- •Лабораторна робота № 13-14
- •І. Теоретичний матеріал
- •1. Постановка задачі інтерполювання функцій
- •Геометричний смисл задачі інтерполювання функцій
- •3. Лінійне і квадратичне інтерполювання
- •4. Параболічне інтерполювання. Інтерполяційна формула Лагранжа
- •6. Екстраполювання функцій
- •7. Засоби інтерполювання функцій в системах комп’ютерної математики
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •Іv. Контрольні запитання
- •Лабораторна робота № 15-16
- •І. Теоретичний матеріал
- •1. Засоби наближення функцій в системі комп’ютерної математики Mathcad
- •1.1. Лінійна регресія (Linear regression)
- •1.2. Поліноміальная регресія (Polynomial regression)
- •1.3. Спеціальні регресії (Specialized regression)
- •1.3.1. Експоненціальна регресія
- •1.3.2. Тригонометрична регресія
- •1.3.3. Логарифмічна регресія
- •1.3.4. Степенева регресія
- •Іі. Завдання до лабораторної роботи
- •Розв’язування
- •Ііі. Індивідуальні завдання
- •Лабораторна робота № 17-18
- •І. Теоретичний матеріал
- •1. Загальні положення щодо програмування у скм
- •2. Процедурне програмування в скм Mathcad
- •Іі. Завдання до лабораторної роботи
- •3. Приклади програм в скм Mathcad
- •Ііі. Індивідуальні завдання
- •IV. Завдання для самостійного виконання
- •Самостійна робота
- •І. Теоретический материал
- •1. Можливості sMath Studio
- •3. Основні елементи інтерфейсу скм sMath Studio
- •4. Встановленн програми sMath Studio
- •5. Основи работи в програмі
- •6. Довідкова інформація
- •Іі. Завдання до лабораторної роботи
- •Ііі. Індивідуальні завдання
- •І. Теоретичний матеріал
- •Іі. Задания до лабораторної работи
- •І. Теоретичний матеріал
- •Іі. Задания до лабораторної работи
- •Графіка в MatLab
- •Ііі. Індивідуальні завдання
- •Контрольні питання
- •І. Теоретичний матеріал
- •1. Основи інтерфейсу MatLab
- •2.Засоби контролю робочої області та файлової системи
- •3. Меню системи MatLab
- •4. Програмування в matlab
- •Основи редагування та налагодження m-файлів
- •Основи програмування
- •5. Чисельне рішення нелінійних рівнянь
- •Іі. Задания до лабораторної работи
- •Ііі. Індивідуальні завдання
- •І. Теоретичний матеріал
- •1. Аналітичне інтегрування засобами MatLab.
- •3. Теоретична оцінка похибки чисельного інтегрування
- •4. Чисельне інтегрування
- •5. Чисельне інтегрування засобами MatLab
- •6. Правило Рунге оцінки похибки інтегрування
- •Іі. Задания до лабораторної работи
- •Перелік літератури та інших джерел Базова
- •Допоміжна
- •Інформаційні ресурси
- •Глосарій курсу
- •Про виконання індивідуального завдання № 1
- •Коваленка Віктора Івановича
III. Індивідуальні завдання
Для задач лінійного програмування геометричним методом за допомогою програми EXTREMUM знайти всі опорні плани і оптимальний план:
1.![]() ,
2.
,
2.![]() ,
,
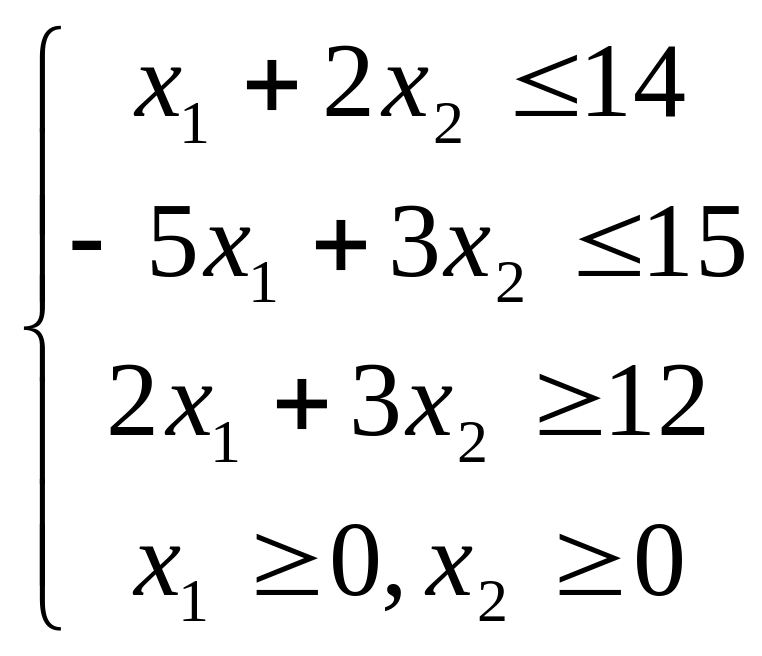 ;
; 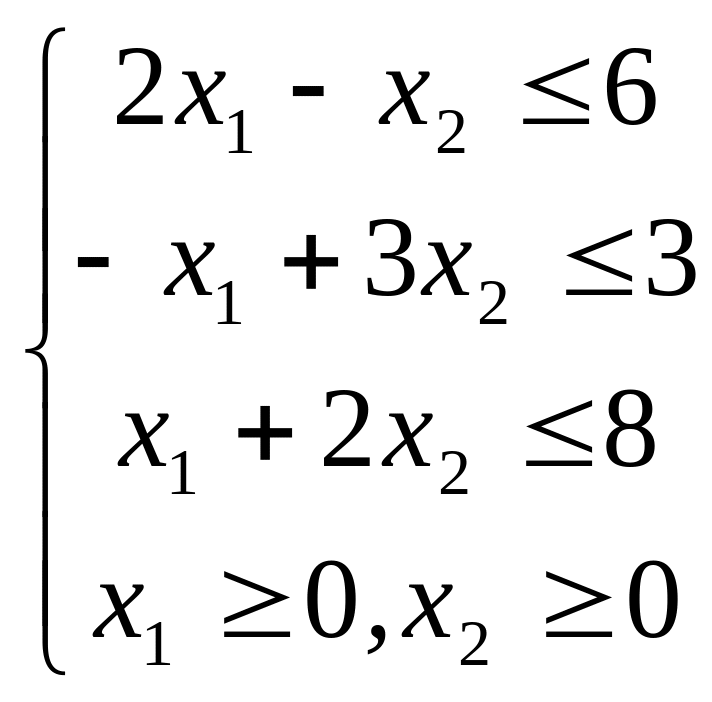 ;
;
3.![]() 4.
4.![]()
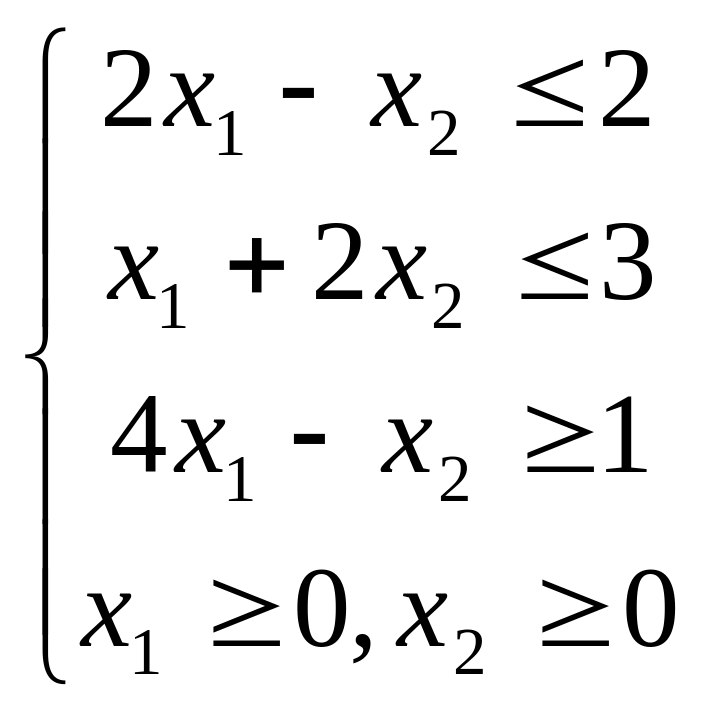 ;
; 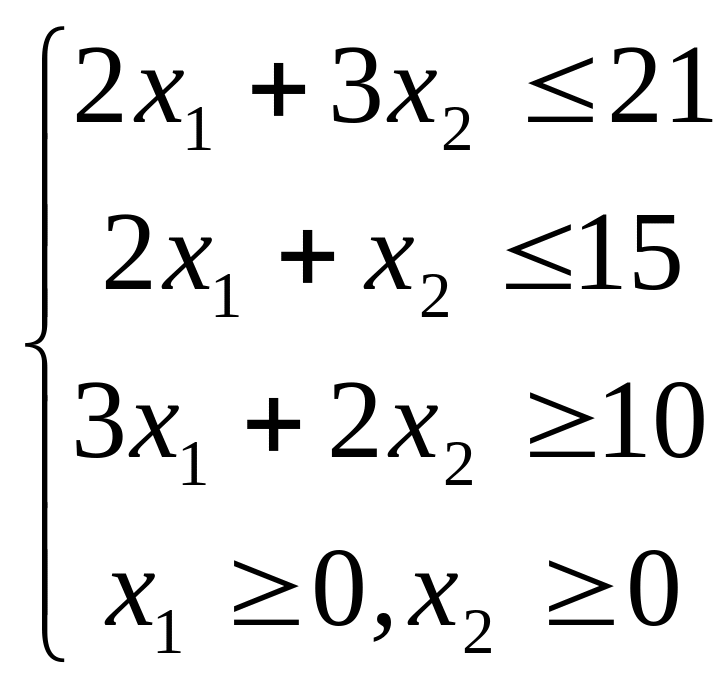 ;
;
5.![]() 6.
6.![]()
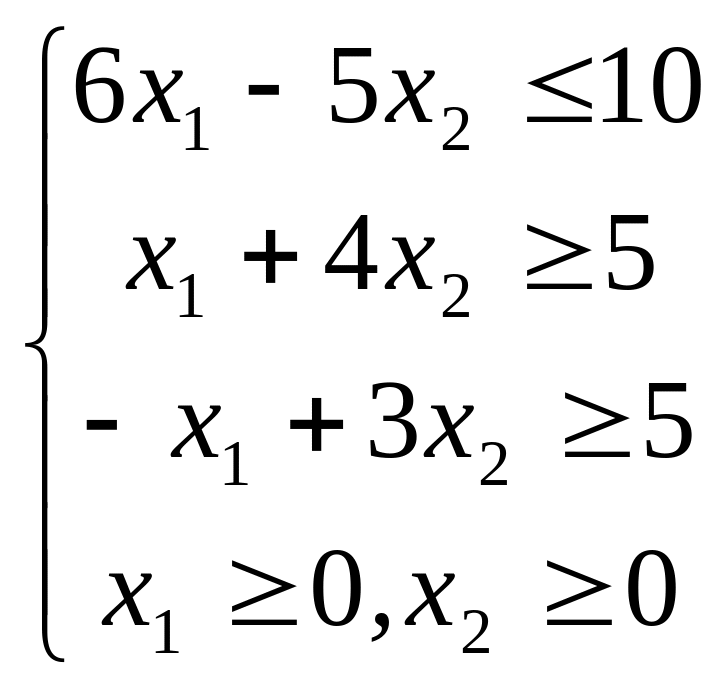 ;
; 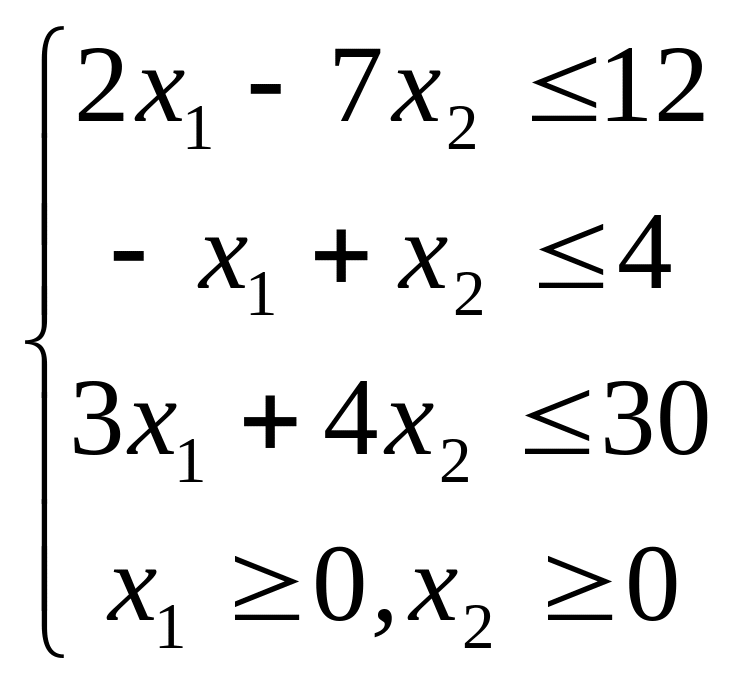 ;
;
7.![]() 8.
8.![]()
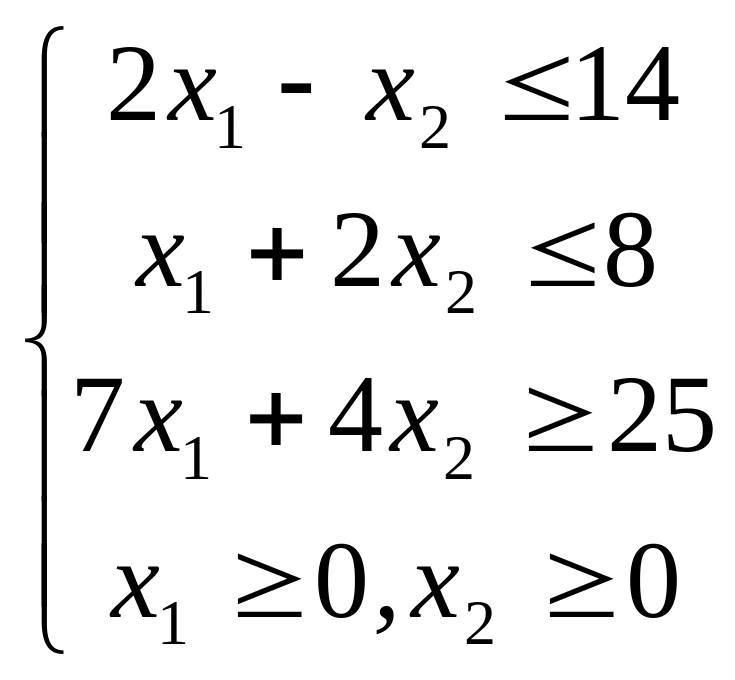 ;
; 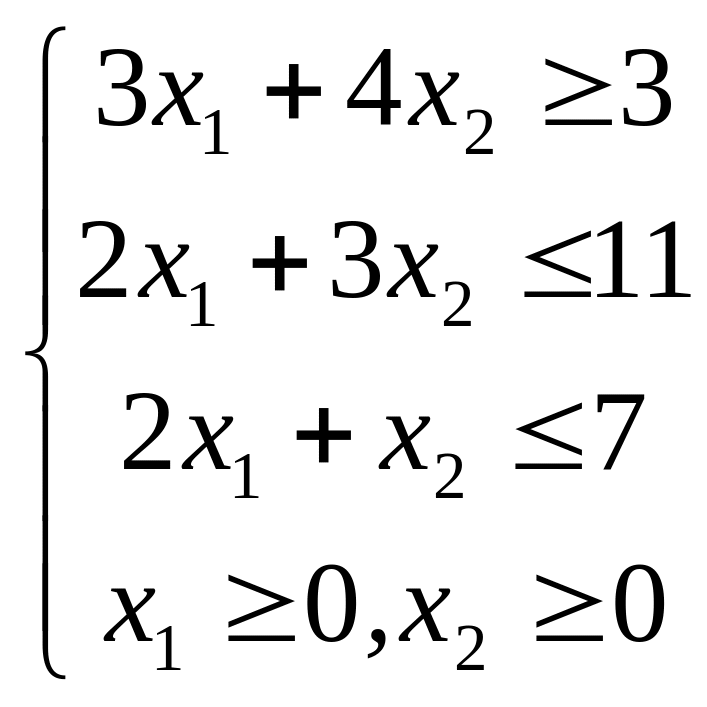 ;
;
9.![]() 10.
10.![]()
 ;
;  .
.
2. За допомогою програми Mathcad задачі з індивідуального завдання розв’язати геометричним методом і за допомогою операторів minimize і maximize. Одержані результати порівняти між собою.
Лабораторна робота № 13-14
Тема: «Параболічне інтерполювання. Інтерполяційна формула Лагранжа»
Питання:
Постановка задачі інтерполювання функцій.
Геометричний смисл задачі інтерполювання функцій.
Лінійна і квадратична інтерполяція.
Параболічне інтерполювання. Інтерполяційна формула Лагранжа.
Приклади інтерполювання функцій.
Екстраполювання функцій.
Засоби інтерполювання функцій в системах комп’ютерної математики.
І. Теоретичний матеріал
1. Постановка задачі інтерполювання функцій
З усіх способів задання функції найбільш зручним у багатьох випадках є аналітичний спосіб у вигляді формули. Цей спосіб дає можливість обчислити значення функції для будь-якого фіксованого значення аргументу, а отже, і скласти таблицю її значень у деяких точках. Складання таблиці значень функції називають табулюванням функції.
У практичних задачах значення функції, що представляють деяку фізичну величину, часто одержують у результаті експерименту у вигляді таблиці або графіка. Досить часто виникає необхідність знайти значення функції при значеннях аргументів, що відсутні в таблиці. Така задача, яку образно можна назвати задачею «читання таблиці між рядками», й одержала назву задачі інтерполювання (inter – між, polio – прикладати).
Задача інтерполювання функції розв’язується шляхом побудови деякого аналітичного виразу, який співпадає зі значеннями таблично заданої функції в скінченній кількості табличних значень аргументу.
Тому, задача інтерполювання функції в деякому розумінні обернена до задачі табулювання функції: при табулюванні від аналітичного способу задання функції переходять до табличного, а при інтерполюванні – за табличними значеннями функції будується деякий аналітичний вираз, тобто формула, що задає шукану функцію наближено.
Постановка задачі.
Нехай деяка функція задана таблично,
тобто для заданих значень аргументу
![]() задані значення функції
задані значення функції
![]()
![]() .
.
Треба знайти аналітичний вираз деякої
функції
![]() ,
котра наближала би дану функцію
,
котра наближала би дану функцію
![]() ,
тобто у точках
,
тобто у точках
![]() приймала би значення
приймала би значення
![]()
![]() :
:
![]() .
.
Геометричний смисл задачі інтерполювання функцій
Г еометричний
смисл задачі інтерполювання функцій
полягає у тому, щоб знайти деяку криву
еометричний
смисл задачі інтерполювання функцій
полягає у тому, щоб знайти деяку криву
![]() ,
котра проходила би через задану систему
точок
,
котра проходила би через задану систему
точок
![]() (рис. 1).
(рис. 1).
Рис. 1.
Інтуїтивно зрозуміло, що через задані
точки можна провести нескінченну
кількість різних кривих. Отже, задача
відшукання функції
![]() за скінченною кількістю її значень є
невизначеною.
за скінченною кількістю її значень є
невизначеною.
Але ця задача стає однозначною, якщо в
якості наближеної функції
![]() для функції
для функції
![]() ,
заданної
,
заданної
![]() -им
своїм значенням, обрати многочлен
-им
своїм значенням, обрати многочлен
![]()
степені
![]() ,
що задовольняє таким умовам:
,
що задовольняє таким умовам:
1) в точках
значення многочлена
![]() співпадає зі значеннями функції
співпадає зі значеннями функції
![]() ,
тобто
,
тобто
![]() ;
;
2) в будь-якій іншій точці
![]() виконується наближена рівність
виконується наближена рівність
![]() .
.
Інтерполювання за допомогою алгебраїчних
многочленів називається поліноміальним
або параболічним інтерполюванням,
многочлен
називається інтерполяційним многочленом,
а точки
![]() називаються вузлами інтерполювання.
називаються вузлами інтерполювання.
Отже, основна ідея інтерполювання полягає в заміні функції, заданої таблицею її значень, інтерполяційним многочленом, що являє собою наближений аналітичний вираз даної функції . Одержаний інтерполяційний многочлен використовують не лише для аналітичного наближення таблично заданої функції, але й у тому випадку, якщо функція задана досить складним аналітичним виразом, яким незручно користуватися в процесі розрахунків, диференціювання або інтегрування.
Розглянемо математичні основи інтерполювання функцій.
