Іі. Завдання до лабораторної роботи

1. Опрацювати теоретичний матеріал.

2. Розв’язати задачу лінійного програмування за допомогою програми EXTREMUM.

Задача

Для виробництва столiв та шаф фабрика використовує певнi ресурси. Норми витрат ресурсiв на один вироб даного виду, прибуток вiд реалiзацiї одного виробу та загальна кiлькiсть наявних ресурсiв наведено в таблицi:

Ресурси	Норми витрат ресурсів на один вироб		Загальна кількість ресурсів
	Стіл	Шафа
Дерево (м2): I вида II вида Трудомісткість (людино-год.)	2 1 15	1 4 12	450 700 3732
Прибуток від реалізації одного виробу (ум.од.)	18	24

Визначити скiльки столiв та шаф необхiдно виготовити фабрицi, щоб прибуток вiд їх реалiзацiї був максимальним.

Розв’язування. Математична модель даної задачі має такий вигляд:

,

Отже поставлена задача є стандартною задачею лінійного програмування,

Процес розв’язування задачі за допомогою програми EXTREMUM відбувається за наведеним вище алгоритмом.

1. За допомогою меню програми «Модель» (в режимі «Задача лінійного програмування») і команди «Редагування моделі» ввести математичну модель задачі (мал. 3).

Після введення даних модель задачі матиме вигляд, який подано на мал. 4.

2. В меню «Побудова» вибрати команду «Прямих», за допомогою якої автоматично будуються прямі, які відповідають обмеженням-нерівностям задачі (мал. 5).

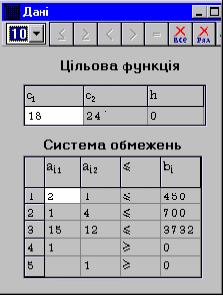
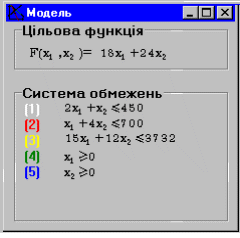
Рис. 3. Рис. 4.

3. За допомогою команди «Півплощин» в меню «Побудова», використовуючи «мишку», визначити півплощини, які відповідають обмеженням-нерівностям задачі (мал. 6).

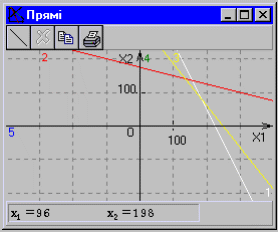
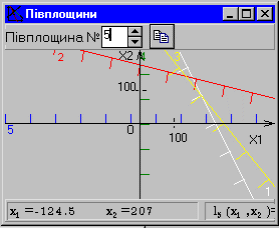
Рис. 5. Рис. 6.

4. За допомогою команди «Многокутника» в меню «Побудова», побудувати многокутник допустимих розв’язків, який є перетином знайдених півплощин, вказуючи «мишкою” його вершини (мал. 7). Як видно з мал. 7, многокутник допустимих розв’язків є обмеженим і опуклим, тому розв’язок задачі існує і міститься на його межі.

5. За допомогою команди «Лінії рівня» в меню «Побудова», визначити координати точки максимуму цільової функції на допустимій множині та обчислити значення функції в цій точці.

Для цього за допомогою «мишки” треба переміщувати лінію рівня в напрямку вектора . Як видно з мал. 8, точкою максимуму цільової функції на допустимій множині є точка перетину прямих з номерами 2 і 3. Згідно графічного розв’язку вона має координати (136;141.5), а цільова функція в ціі точці набуває значення 5844. Отже знайдено наближений розв’язок поставленої задачі.

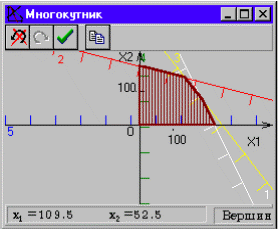
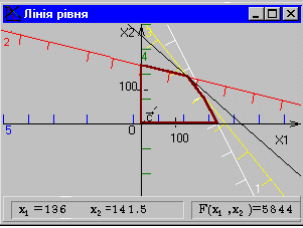
Рис. 7. Рис. 8.

Для уточнення результатів треба скористатися командою «Числове уточнення». Для цього необхідно вказати номери прямих, на перетині яких міститься шукана точка (мал. 9). Розв’язком задачі є при , .

Рис. 9.

3. За допомогою програми Mathcad розв’язати попередню задачу і порівняти результати з результатами, одержаними геометричним методом. 

4. Виконати індивідуальне завдання.

5. Оформити звіт про виконання лабораторної роботи.