Іv. Контрольні запитання
Записати правила диференціювання і таблицю похідних для елементарних функцій.
Сформулювати теорему Вейєрштрасса про існування найбільшого і найменшого значень функцій від однієї змінної на відрізку і проаналізувати її.
Дати означення локального і глобального екстремумів (максимуму і мінімуму).
В чому полягає суть необхідних і достатніх умов екстремуму.
Сформулювати теорему Ферма про необхідні умови екстремуму. Навести приклад, коли похідна функції в точці дорівнює 0, але точка не є точкою екстремуму.
Які точки називають стаціонарними?
Сформулювати достатні умови екстремуму в термінах першої похідної.
Сформулювати достатні умови екстремуму в термінах другої похідної.
Сформулювати загальне правило відшукання найбільших і найменших значень функції на відрізку.
Сформулювати теорему Вейєрштрасcа про існування найбільшого і найменшого значень функцій від багатьох змінних.
Сформулювати узагальнену теорему Ферма про необхідні умови екстремуму.
Сформулювати достатні умови екстремуму для функції від двох змінних.
Сформулювати загальне правило відшукання найбільших і найменших значень функції від багатьох змінних у всьому просторі.
Лабораторна робота № 11-12
Тема: «Геометричний метод розв’язування задачі лінійного програмування»
Питання:
Геометрична інтерпретація стандартної задачі лінійного програмування.
Геометричний метод розв’язування задачі лінійного програмування.
Розв’язування практичних задач.
Програмне забезпечення: програма EXTREMUM.
І. Теоретичний матеріал
Розглянемо геометричну інтерпретацію стандартної задачі лінійного програмування.
Задача оптимізації виду
, (1)
, (2)
,
де
для
називається загальною задачею
лiнiйного програмування.
Якщо допустима множина визначається обмеженнями виду
, (3)
то задача (1), (3) називається стандартною.
Особливість геометричної інтерпретації
двовимірної задачі лінійного програмування
полягає в тому, що, по-перше, лінія рівня
цільової функції
є пряма, при цьому градієнт функції
(вектор 
)
є напрямом її найшвидшого зростання,
по-друге, якщо задача має розв’язок, то
він досягається обов’язково на межі
допустимої множини X, яка в цьому
випадку являє собою обмежену многокутну
область, а сам розв’язок задачі є або
деяка вершина многокутника
(мал. 1 а)
або множина точок деякої його
сторони
(мал.1 б).
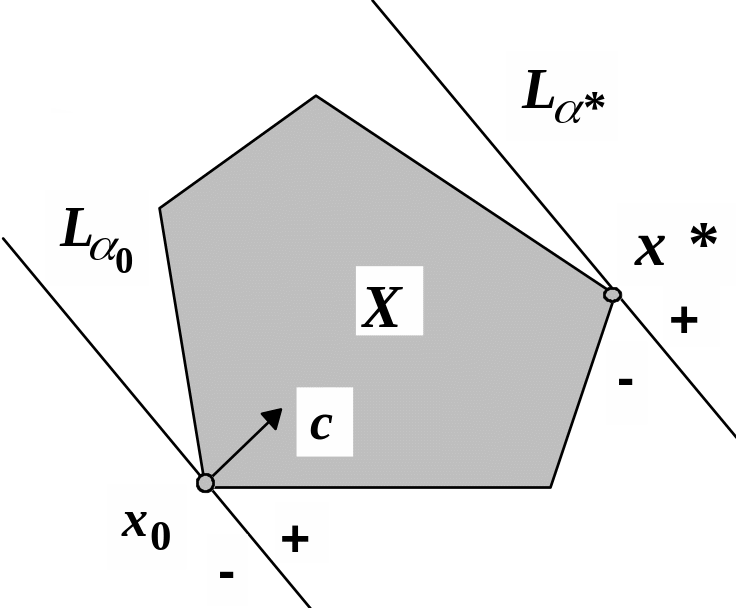
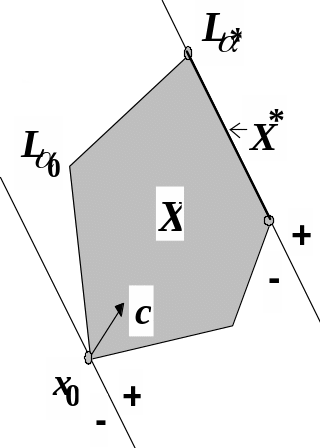
а) б)
Рис. 1. Геометричну інтерпретація задачі лінійного програмування
Наведемо алгоритм розв’язування стандартної двовимірної задачi лiнiйного програмування геометричним методом.
АЛГОРИТМ розв’язування стандартної двовимірної задачi лiнiйного програмування геометричним методом
1. Побудувати прямi, рiвняння яких одержуються внаслiдок замiни в обмеженнях (3) знакiв нерiвностей на знаки рiвностей.
2. Знайти пiвплощини, якi визначаються кожним з обмежень-нерівностей задачi.
3. Знайти многокутник допустимих розв’язкiв.
Побудувати пряму
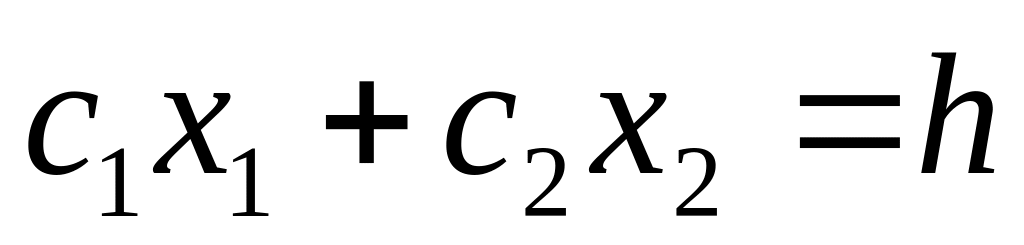(лінію рівня цільової функції), при
цьому величина h
підбирається так, щоб лінія рівня
проходила через многокутник допустимих
розв’язкiв.
Побудувати вектор
.
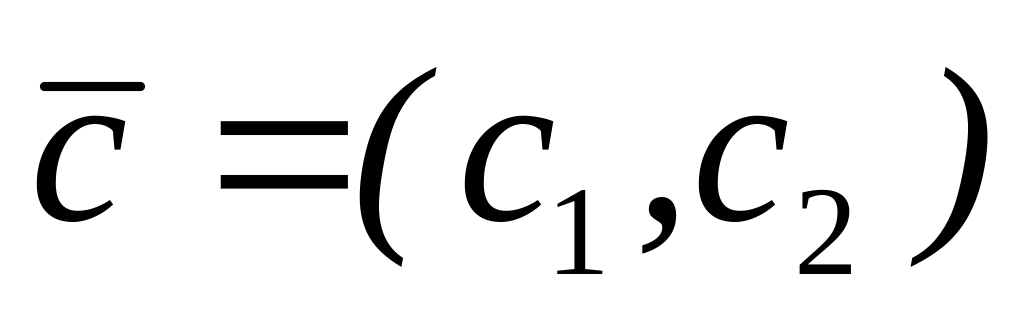Рухаючи пряму в напрямку вектора
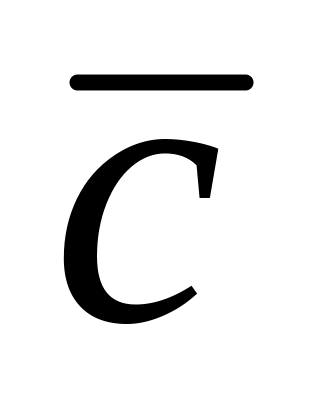при розв’язанні задачі максимізації
(або в зворотньому напрямку при
розв’язанні задачі мінімізації), знайти
точку (множину точок), де цiльова функцiя
приймає максимальне (мiнiмальне) значення,
або встановити необмеженiсть зверху
(знизу) функцiї на допустимій множинi
(див. мал.2).
7. Якщо існує единий розв’язок задачі, визначити координати знайденої точки i обчислити значення цiльової функцiї в цiй точцi. Якщо існує безліч розв’язків, то визначити координати принаймні однієї екстремальної точки i обчислити значення цiльової функцiї в цiй точцi.
Рис.2.