5. Розв’язування задач математичного програмування в середовищі Mathcad

Приклад 2. Знайти розв’язок екстремальної задачі в середовищі Mathcad:

,

.

Розв’язування.

Маємо задачу лінійного програмування від двох змінних. Розглянемо два можливих способи розв’язування даної задачі. У першому варіанті (рис. 3) обмеження задаються у такому ж вигляді, як і в умові задачі, а у другому (рис. 4) – обмеження задаються у матричному вигляді. Щоб задати обмеження в матричному вигляді треба записати матрицю коефіцієнтів і вектор-стовпчик вільних членів для системи обмежень:

, .

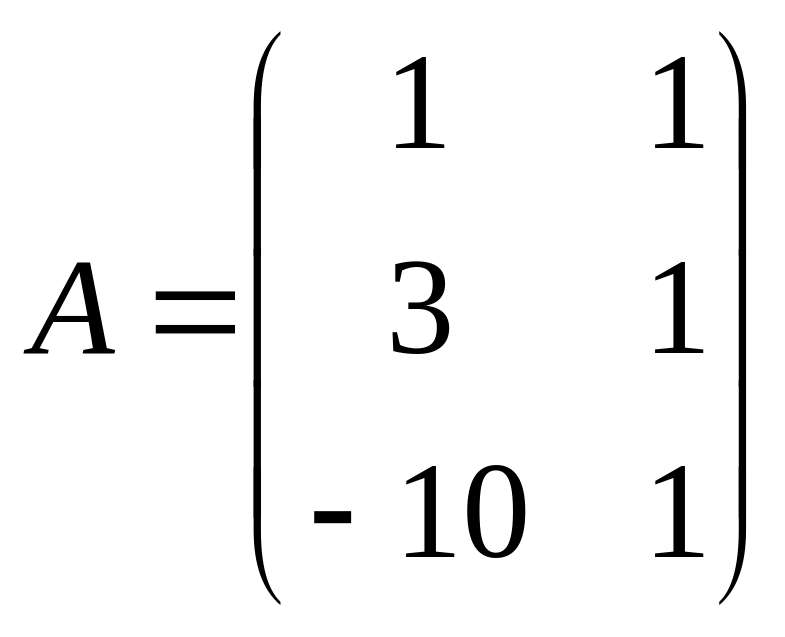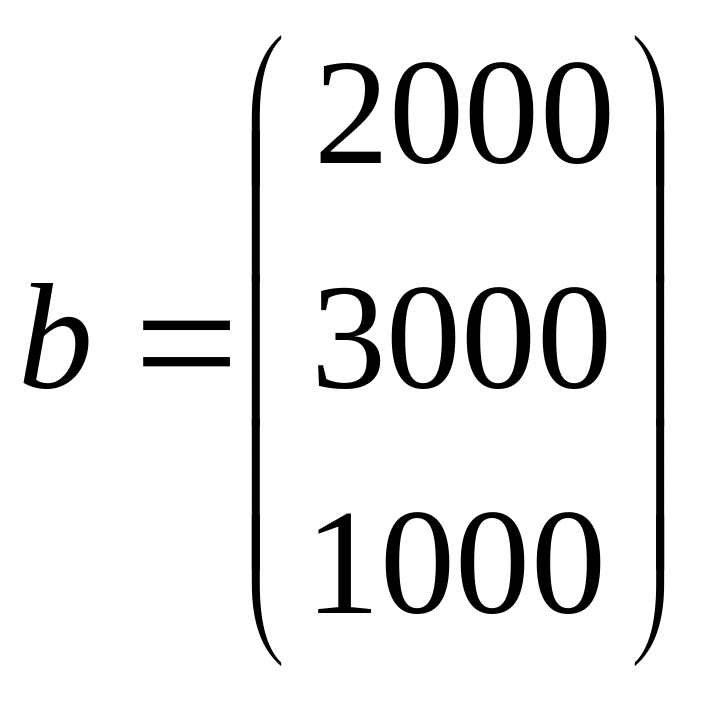Тоді обмеження задачі будуть мати більш компактний вигляд:

Як видно з рис. 3 та 4 в результаті обчислень одержуються однакові оптимальні точки. Але матричний спосіб запису обмежень надає можливість значно зекономити час на запис умови задачі, особливо, при великій кількості змінних.

Рис. 3. Розв’язок задачі лінійного програмування від двох змінних

Рис. 4. Розв’язок задачі лінійного програмування від двох змінних

Приклад 3. Знайти розв’язок транспортної задачі в середовищі Mathcad.

У трьох пунктах постачання зосереджений однорідний вантаж в обсязі 420 т, 380 т і 400 т. Цей вантаж необхідно перевезти в три пункти призначення відповідно в обсязі 260 т, 520 т і 420 т. Вартості перевезення (в грн) однієї тони вантажу з кожного пункту постачання до кожного пункту призначення є відомими величинами і задаються матрицею

.

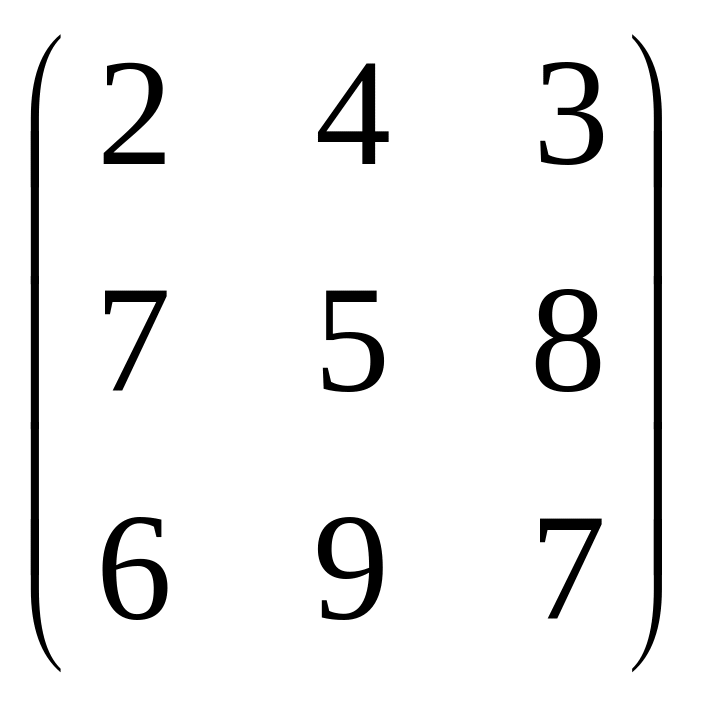Знайти план перевезень, який забезпечує вивезення наявного в пунктах постачання вантажу і завезення його до пунктів призначення в необхідній кількості при мінімальній загальній вартості перевезень.

Для транспортної задачі її умову зручно подавати у табличній формі:

Таблиця 1.

Пункти	Пункти призначення			Запаси (т)
постачання	B1	B2	B3
A1	2	4	3	420
A2	7	5	8	380
A3	6	9	7	400
Потреби (т)	260	520	420

Побудуємо математичну модель цієї задачі. Позначимо через – кiлькiсть одиниць вантажу, яку заплановано перевезти з -го пункту постачання до -го пункту призначення, де , . Тодi план перевезень можна записати у вигляді матриці

,

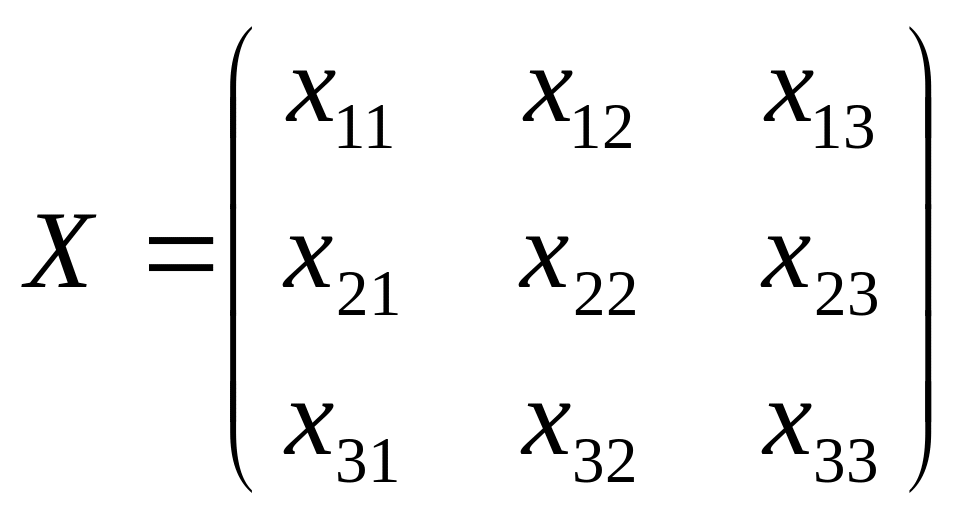при цьому загальна вартiсть перевезення вантажу буде дорiвнювати

i її потрiбно мiнiмiзувати.

За умовою задачі необхідно вивезти весь вантаж з пунктів постачання, тому план перевезень повинен задовольняти такі умови

а оскільки, крім того, необхідно повністю задовольнити потреби пунктів призначення, то план перевезень повинен також задовольняти умови

Враховуючи те, що за планом вантаж може бути перевезено з -го пункту постачання до -го пункту призначення або ні, то на змінні накладається умова:

, , .

Відомо, що для того щоб транспортна задача мала розв’язок, необхідно і достатньо щоб були рівними запаси вантажу і його потреби (умова замкненості задачі). Перевіряючи умову замкненості транспортної задачі, тобто обраховуючи сумарні запаси і потреби, маємо: т, т. Отже задача є замкненою і тому має розв’язок, який знайдемо за допомогою пакету Mathcad.

Щоб розв’язати транспортну задачу в середовищі Mathcad потрібно скласти матрицю вартостей перевезень одиниці товару для замкненої задачі, а також записати вектори-стовпчики запасів і потреб.

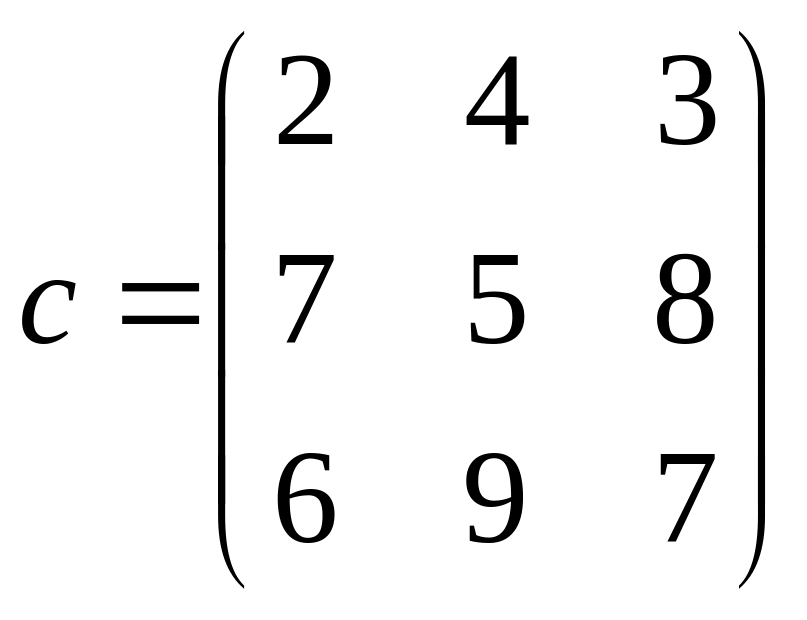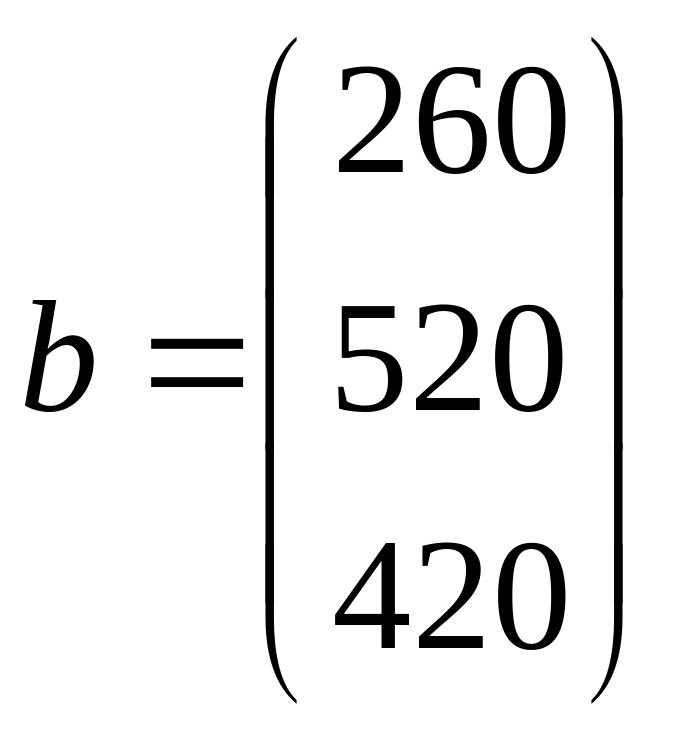Матриця вартостей c буде мати вигляд: . Вектори-стовпчики запасів і потреб дорівнюють відповідно: , . Далі складаємо математичну модель задачі, тобто цільову функцію та систему обмежень, задаємо початкове наближення та отримуємо розв’язок (рис. 5).

Рис. 5. Приклад розв’язку транспортну задачу в середовищі Mathcad

Зауваження. При розв’язуванні даної задачі потрібно в контекстному меню, викликаному для команди Minimize, вказати метод лінійної ітерації, тобто вибрати пункт Linear.