3. Класичний метод знаходження екстремумiв функцiї багатьох змiнних

Сформулюємо спочатку умови iснування екстремумiв для функцiї багатьох змiнних в n-вимiрному евклiдовому просторi. Для цього нагадаємо декілька важливих понять і означень.

Означення 3. Множина впорядкованих наборів з n дiйсних чисел, тобто множина n-вимiрних векторiв (точок) з дiйсними координатами , в якiй вiдстань мiж двома точками i визначається за формулою

,

називається n-вимiрним евклiдовим простором i позначається .

Означення 4. Нехай точка i r – деяке додатне число. Множина точок

називається n-вимiрною замкненою кулею радiуса r з центром в точцi О,

а множина точок

,

називається n-вимiрною вiдкритою кулею радiуса r з центром в точцi О.

Вiдкрита куля радiуса з центром в точцi О називається околом точки О .

Нехай X – деяка множина точок простору .

Означення 5. Точка x називається внутрiшньою точкою множини X, якщо iснує окіл точки x, який повнiстю лежить у множинi X .

Множина всiх внутрiшнiх точок множини X утворює внутрiшнiсть цiєї множини i позначається int X:

.

Означення 6. Множина X називається вiдкритою, якщо всi її точки внутрiшнi, тобто якщо .

Означення 7.  Точка x називається граничною точкою множини , якщо будь-який окіл точки x мiстить нескiнченну множину точок з множини .

Множина всiх граничних точок множини X утворює замикання цiєї множини i позначається .

Означення 8. Множина X називається замкненою, якщо вона мiстить всi свої граничнi точки, тобто якщо .

Означення 9. Множина X називається обмеженою, якщо iснує замкнена куля скінченного радіуса, що мiстить всi точки множини X.

Функцiю від змінних будемо записувати так .

Теорема  7 (Вейєрштрасса). Якщо функцiя визначена і неперервна на обмеженій і замкненій множинi з простору , то вона досягає на цій множині своїх найменшого i найбiльшого значень.

Нехай функцiя визначена в деякому околi точки .

Теорема 8 (необхiдна умова екстремуму). Якщо функцiя в точцi має екстремум i скінченні частиннi похiднi першого порядку за аргументами , то

.

Наслiдок. Якщо функцiя має в точцi екстремум i диференцiйована в цiй точцi, то

(при будь-яких значеннях диференцiалiв незалежних змiнних ).

Точки, в яких перший диференцiал функцiї дорiвнює нулевi, називають стацiонарними або точками можливого екстремуму цiєї функцiї.

Щоб знайти точки можливого екстремуму функцiї , треба розв’язати систему рiвнянь

.

Для формулювання достатнiх умов екстремуму нагадаємо деякi факти з лiнiйної алгебри.

Функцiя виду

,

де - числа з , , називається квадратичною формою вiд змiнних . Числа називаються коефiцiєнтами квадратичної форми, а складена з цих коефiцiєнтiв симетрична матриця

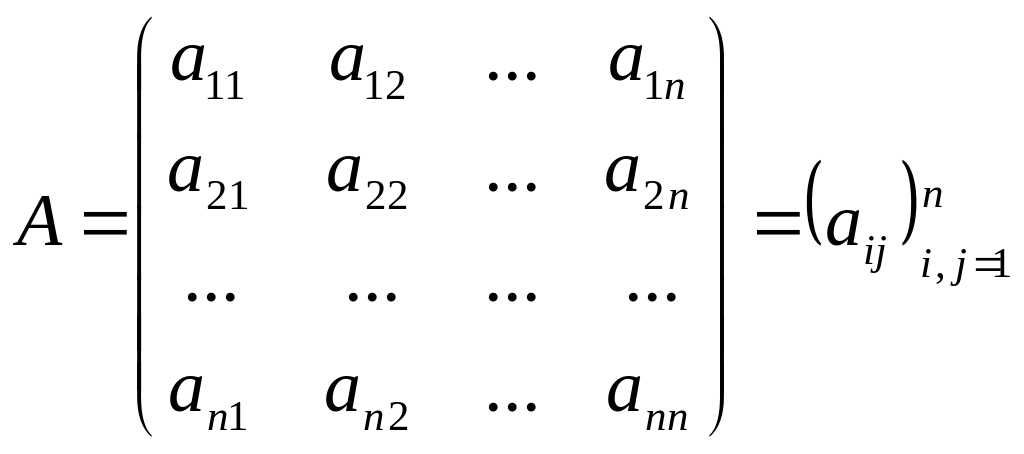
називається матрицею квадратичної форми .

Визначники

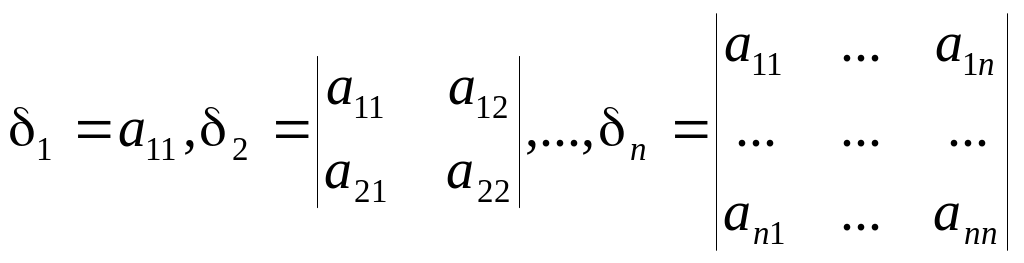
називаються кутовими мiнорами матрицi A.

В матричному поданні квадратична форма має вигляд

.

Квадратична форма називається додатно визначеною, якщо вона набуває додатних значень, тобто

,

для будь-яких значень змiнних , якi одночасно не дорiвнюють нулевi. Зазначимо, що .

Квадратична форма називається від’ємно визначеною, якщо вона набуває відє’мних значень для будь-яких значень змiнних , якi одночасно не дорiвнюють нулевi.

Наприклад, - додатно визначена квадратична форма, оскiльки в усiх точках , крiм точки (0,0).

Квадратична форма називається знаковизначеною, якщо вона є або додатно визначеною, або вiд’ємно визначеною.

Квадратична форма називається невід’ємно (недодатно) визначеною, якщо вона набуває невiд’ємних (недодатніх) значень для будь-яких значень змiнних , але при цьому значення нуль набуває не тiльки при .

Квадратична форма називається квазізнаковизначеною, якщо вона є або невiд’ємно визначеною, або недодатно визначеною.

Наприклад, - квазiзнако-визначена (невід’ємно визначена) квадратична форма, оскiльки в усiх точках , але не тiльки в точцi (0,0), а й у всiх точках прямої .

Квадратична форма називається знакозмiнною, якщо вона набуває як додатних, так i вiд’ємних значень.

Наприклад, - знакозмiнна квадратична форма, оскiльки вона набуває як додатних, так i вiд’ємних значень: .

Має місце критерiй Сiльвестра:

1) для того щоб квадратична форма була додатно визначеною, необхiдно i достатньо, щоб всi кутовi мiнори її матрицi були додатнi:

;

2) для того щоб квадратична форма була вiд’ємно визначеною, необхiдно i достатньо, щоб знаки кутових мiнорiв її матрицi чергувались таким чином:

.

В математичному програмуванні часто використовуються відповідні поняття знаковизначеності для симетричних матриць. Симетрична матриця

називається додатно визначеною, якщо квадратична форма

для будь-яких значень змiнних , якi одночасно не дорiвнюють нулевi. Відповідно формулюється і критерій Сільвестра.

Другий диференцiал функцiї , де - незалежнi змiннi, в точцi можна подати у виглядi

.

Цей вираз показує, що другий диференцiал функцiї в точцi є квадратичною формою вiд змiнних , де частиннi похiднi другого порядку (коефiцiєнти квадратичної форми) задовольняють умову

(2)

Матриця других частинних похідних функції в точці

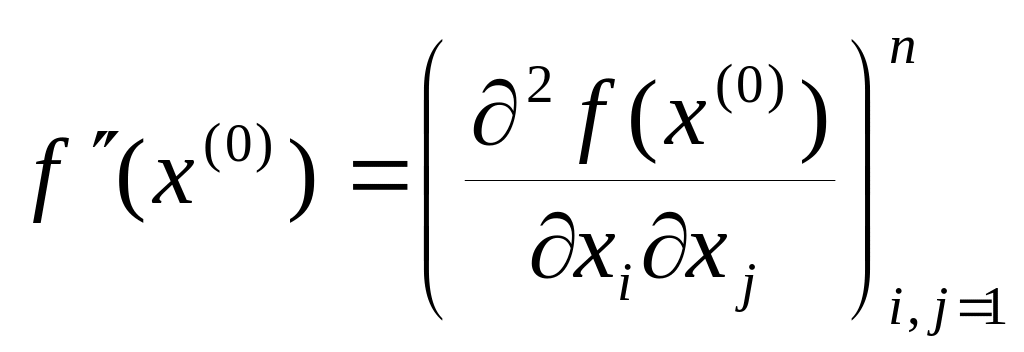
називається матрицею Гессе або гессіаном.

Зауважимо, що умова (2) виконується коли мішані частинні похідні другого порядку, як функції від , є неперервними в точці .

Теорема 9 (достатнi умови екстремуму). Нехай функцiя визначена, неперервна і має неперервні частинні похідні першого і другого порядку в околi деякої стаціонарної точки даної функцiї. Тодi якщо другий диференцiал є додатно (вiд’ємно) визначеною квадратичною формою вiд змiнних , то функцiя має в точцi локальний мiнiмум (максимум). Якщо ж є знакозмiнною квадратичною формою, то в точцi функцiя не має локального екстремуму.

Зауваження. Якщо , а є квазiзнаковизначеною квадратичною формою, то функцiя може мати в точцi локальний екстремум, і може не мати. В цьому випадку треба додатково досліджувати поведінку функції в околі точки , користуючись означенням точок екстремуму або властивостями похідних більш високих порядків. Наприклад, легко перевірити, що для кожної з функцiй i в точцi =(0,0) виконуються умови , , тобто точка - стаціонарна для цих функцій і їх другий диференцiал є квазiзнаковизначеною квадратичною формою. Але при цьому перша функцiя має в точцi =(0,0) локальний мiнiмум (оскільки ), а друга функцiя в цiй точцi не має екстремуму, оскільки для деяких точок з околу точки має значення більші від нуля, в для деяких - менші.

Розглянемо окремо достатнi умови екстремуму для функцiї двох змiнних.

Нехай функцiя визначена, неперервна і має неперервні частинні похідні першого і другого порядку в околi деякої стаціонарної точки даної функцiї.

Введемо позначення:

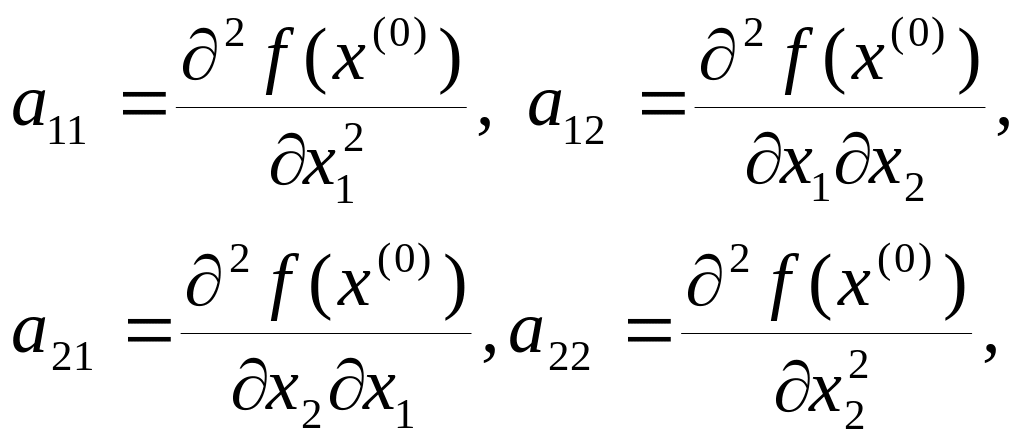
при цьому, згідно припущення, .

З теореми 6 i критерiя Сiльвестра випливає таке твердження:

1) якщо , то в точцi функцiя має локальний екстремум: мiнiмум при i максимум при ;

2) якщо , то в точцi функцiя не має екстремуму;

3) якщо , то в точцi функцiя може мати локальний екстремум, а може й не мати його.

Сформулюємо загальне правило відшукання розв’язкiв багатовимiрних задач безумовної оптимiзацiї.

Правило II.

Нехай функцiя визначена, неперервна i диференцiйовна в усiх точках простору .

Щоб знайти глобальний мiнiмум (максимум) функцiї на всьому просторi , потрiбно:

1) знайти всi стацiонарнi точки функцiї , тобто розв’язати систему рiвнянь

; (3)

2) якщо система (3) не має розв’язкiв, то функцiя не має екстремумiв; якщо система (3) має розв’язки, то провести додаткове дослiдження i визначити, якi з стацiонарних точок є точками локального мiнiмуму (максимуму); при цьому, якщо цiльова функцiя має неперевні частиннi похiднi першого і другого порядку в околi стацiонарної точки, то для такого дослiдження можна використати достатнi умови екстремуму;

3) знайти значення функцiї у точках локального мiнiмуму (максимуму) (якщо такi точки iснують);

4) серед усiх знайдених значень функцiї вибрати найменше (найбiльше).

При розв’язуваннi задач умовної оптимiзацii, коли допустима множина X є пiдмножиною простору , знайти точки екстремуму значно складнiше навiть коли множина X обмежена і замкнена.

Формально загальне правило розв’язування таких задач можна одержати з правила II, замiнивши пункт 4 на такий:

- знайти найменше (найбiльше) значення цiльової функцiї на межi множини X , далі знайти значення, яких функцiя набуває в точках локальних мiнiмумiв (максимумiв), i вибрати найменше (найбiльше) серед усіх так знайдених значень.

Однак класичними методами це вдається зробити лише у випадках, коли множина X має досить просту структуру або задається як множина розв’язкiв деякої системи рiвнянь (принцип Лагранжа).