IV. Завдання для самостійного виконання

1. Обчислити визначники 2-го та 3-го порядків:

1)

2)

3)

2. Розв’язати рівняння та нерівності:

1)

2)

3. Використовуючи властивості визначників, довести рівності:

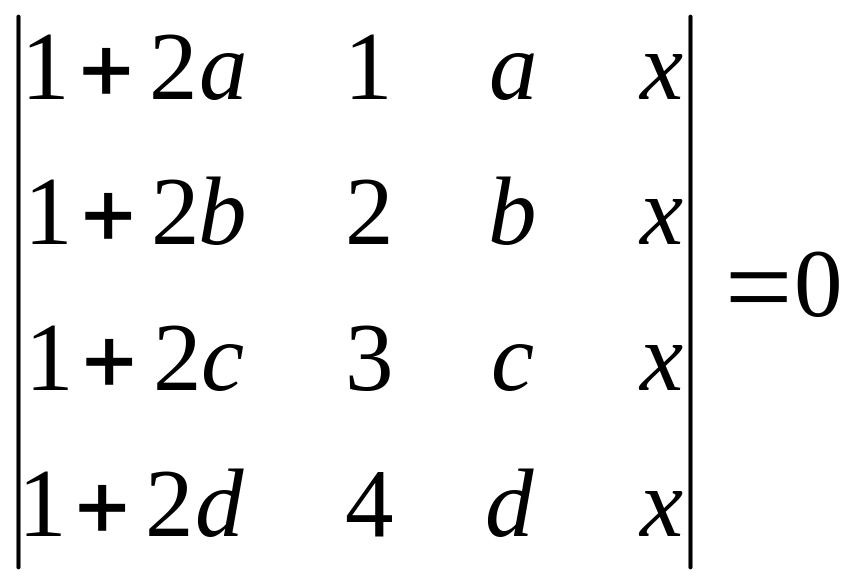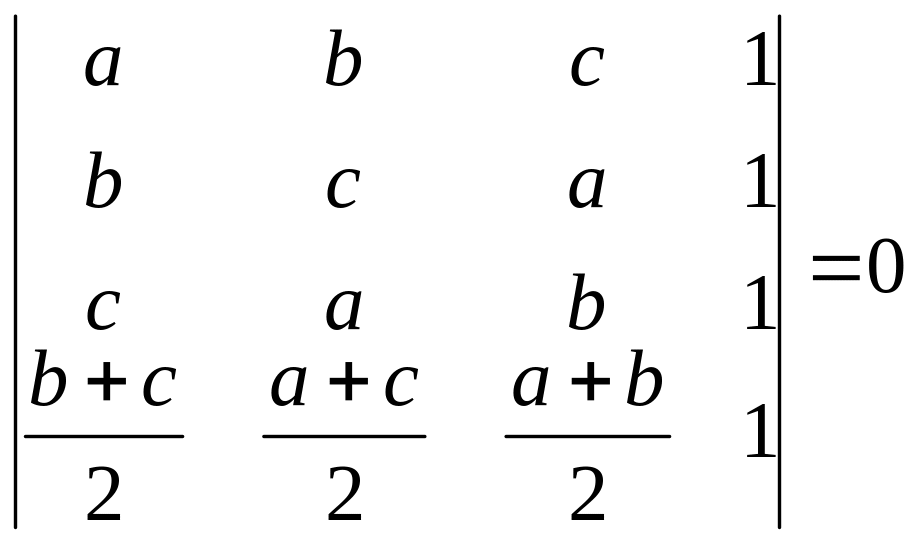1) ; 2) ; 3) .

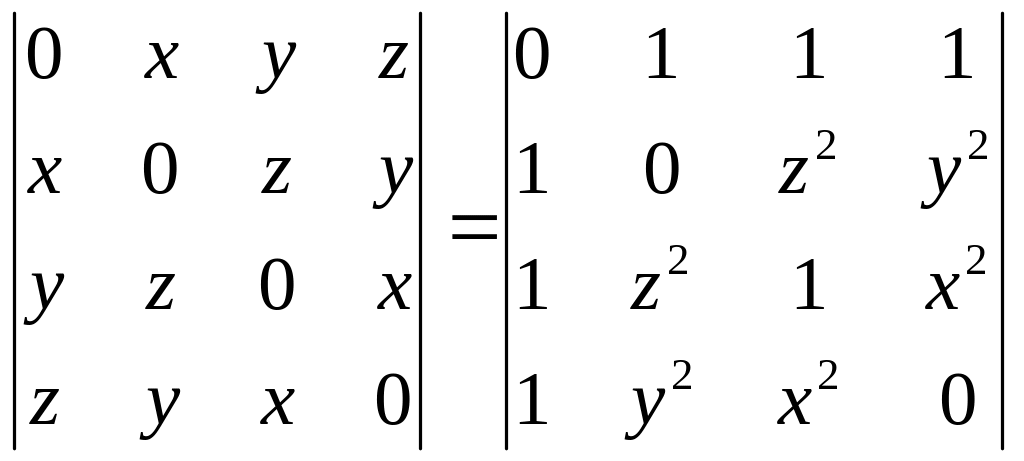4. Обчислити , якщо:

1) і ;

2) і .

5. Знайти , якщо:

1) ;

2) ;

3) .

6. Розв’язати матричні рівняння:

1) ;

2) ;

3) .

7. Дослідити системи на сумісність, використовуючи критерій Кронекера-Капеллі. Якщо система сумісна, то знайти її розв’язок:

1)	2)
3)	4)

8. Розв’язати системи лінійних рівнянь:

1. методом Гауса;

2. методом Крамера;

3. матричним методом.

1)	2)
3)	4)

Лабораторна робота №5-6

Тема: «Основи математичного аналізу в СКМ»

Питання:

1. Знаходження границь за допомогою системи Mathcad.

2. Аналітичне і чисельне диференціювання та їх реалізація в системі Mathcad.

3. Дослідження функцій і побудова їх графіків за допомогою системи Mathcad.

4. Знаходження невизначених і визначених інтегралів за допомогою системи Mathcad.

І. Теоретичний матеріал

1. Знаходження границь функцій

В системі Mathcad обчислення границі функції можливе лише у режимі символьних обчислень за допомогою оператора «lim» і оператора символьного виводу « ». Приклади обчислення границь різних функцій та їх графічна інтерпретація подані на рис. 1.

Рис. 1. Приклад на обчислення границі функції

2. Аналітичне і чисельне диференціювання та їх реалізація в системі Mathcad

В системі Mathcad аналітичне і чисельне диференціювання здійснюється в режимі символьних обчислень за допомогою операторі « » і , які активізується через меню Calculus (рис. 2) і оператора символьного виведення « », який активізується через меню Symbolic.

Рис. 2. Активація меню Calculus та Symbolic

Приклади обчислення похідних за означенням і з використанням вбудованих операторів подано на рис. 3.

Рис. 3. Приклади обчислення похідних

3. Дослідження функцій і побудова їх графіків за допомогою системи Mathcad

Схема повного дослідження функції однієї змінної та побудова її графіка:

1. Знайти область визначення функції.

2. Дослідити функцію на парність, непарність.

3. Дослідити функцію на періодичність.

4. Знайти проміжки монотонності функції.

5. Знайти точки екстремуму функції.

6. Знайти інтервали опуклості (вгнутості) й точки перегину.

7. Знайти асимптоти функції:

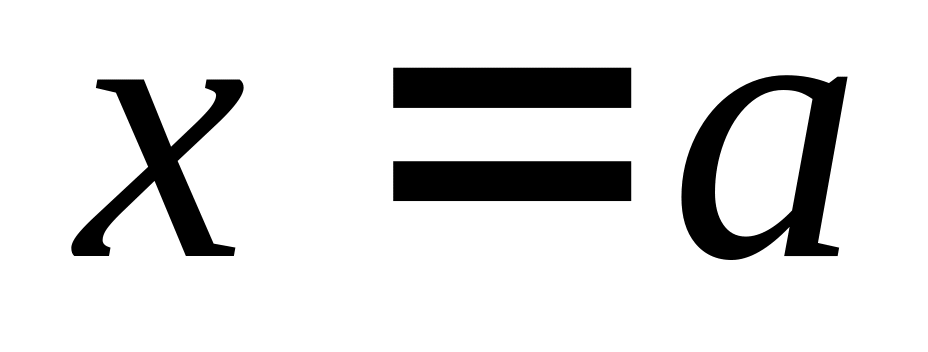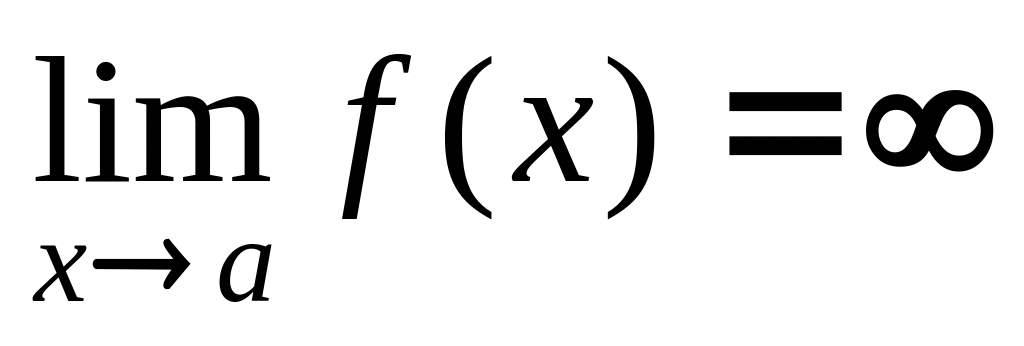   • вертикальні виду , де , або , або ;

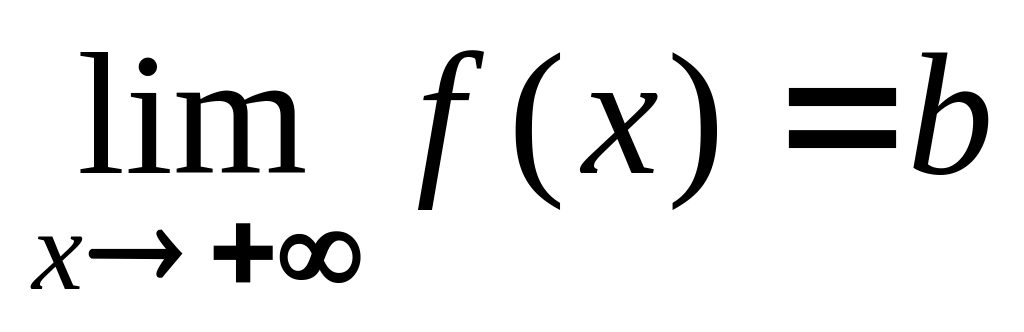   • горизонтальні виду , де , або ;

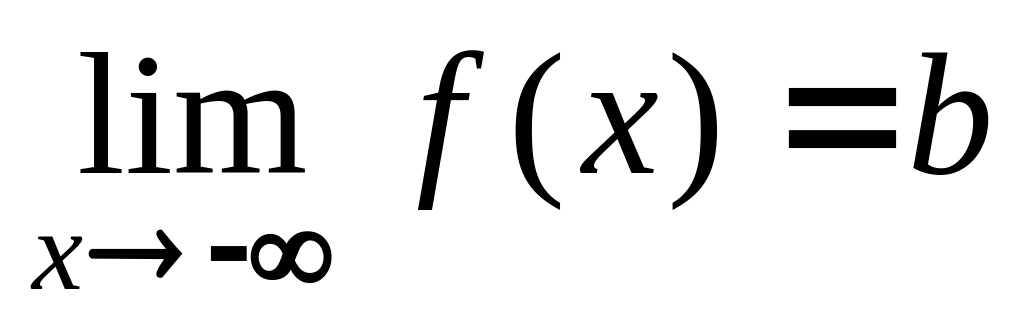   • похилі виду 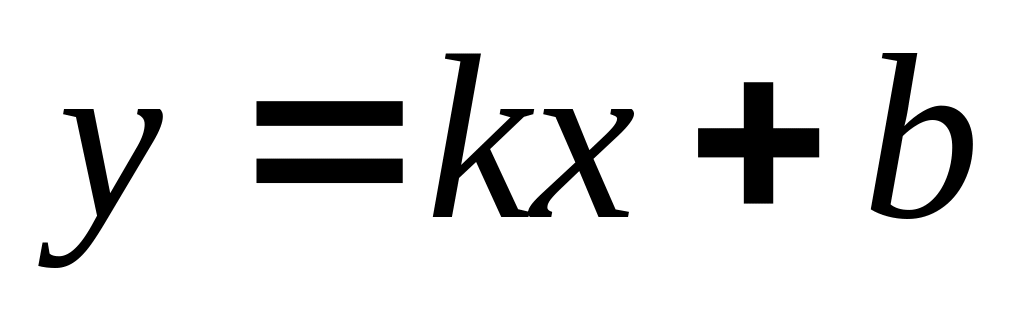, де , .

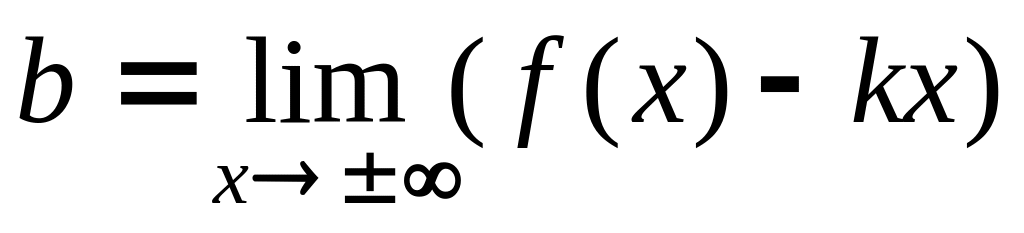8. Знайти точки перетину графіка функції з осями координат та проміжки знакосталості функції.

9. Використовуючи результати дослідження та обчисливши значення функції в кількох контрольних точках, побудувати схему графіка.

Приклад 1. Провести повне дослідження функції і побудувати її графік:

.

Розв’язування.

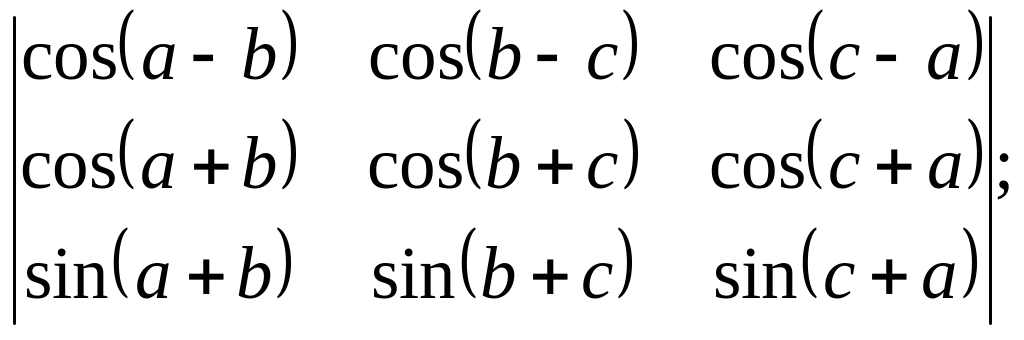
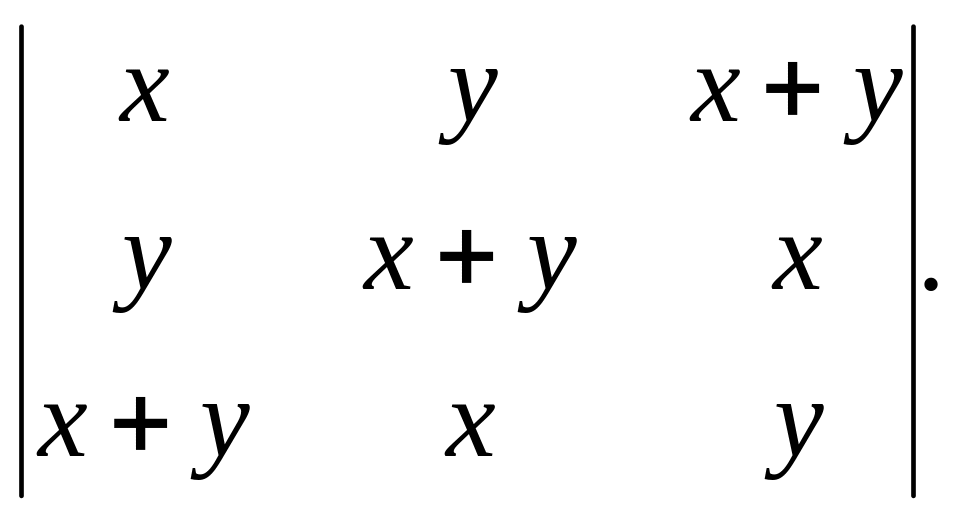
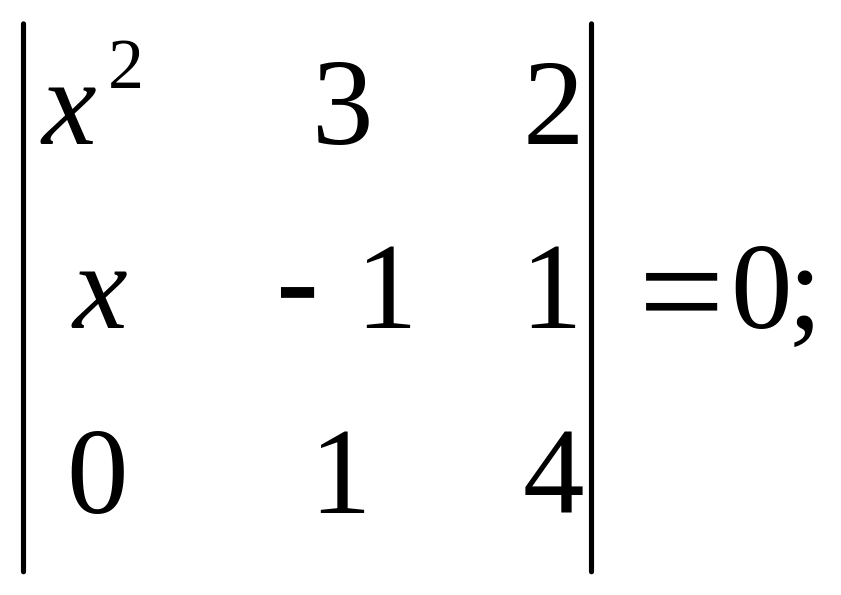
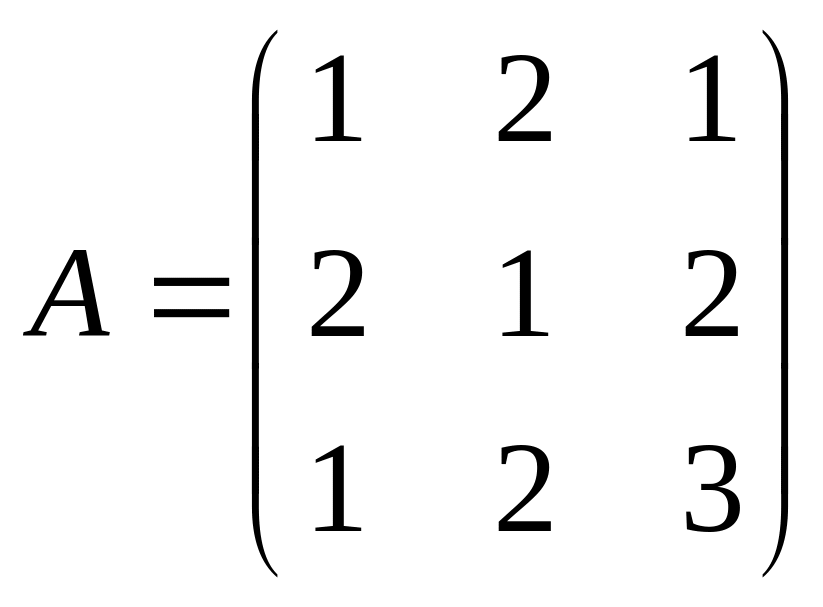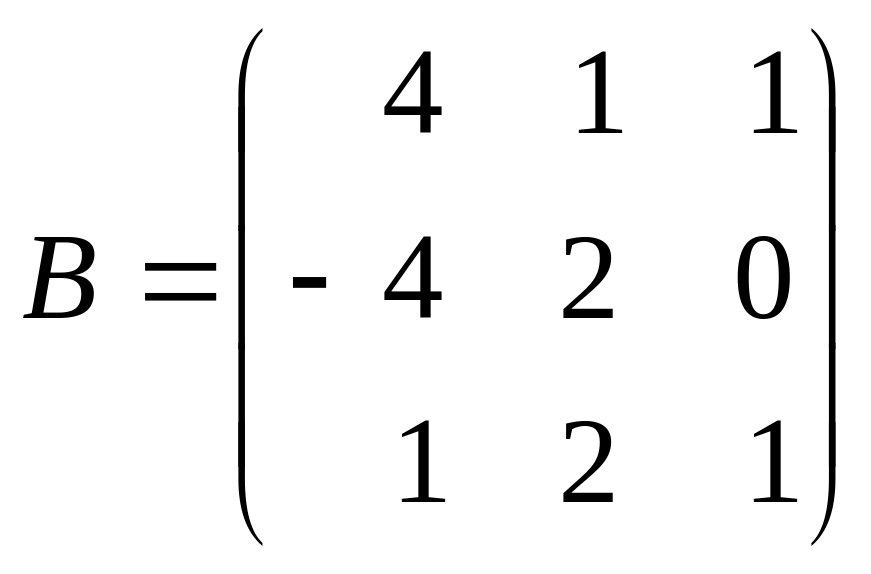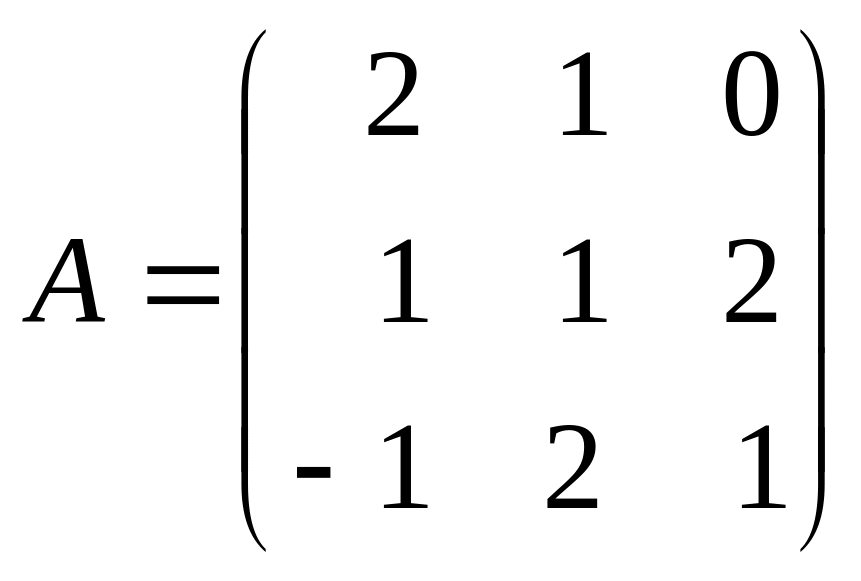Рис. 4. Побудова досліджуваного графіка функції
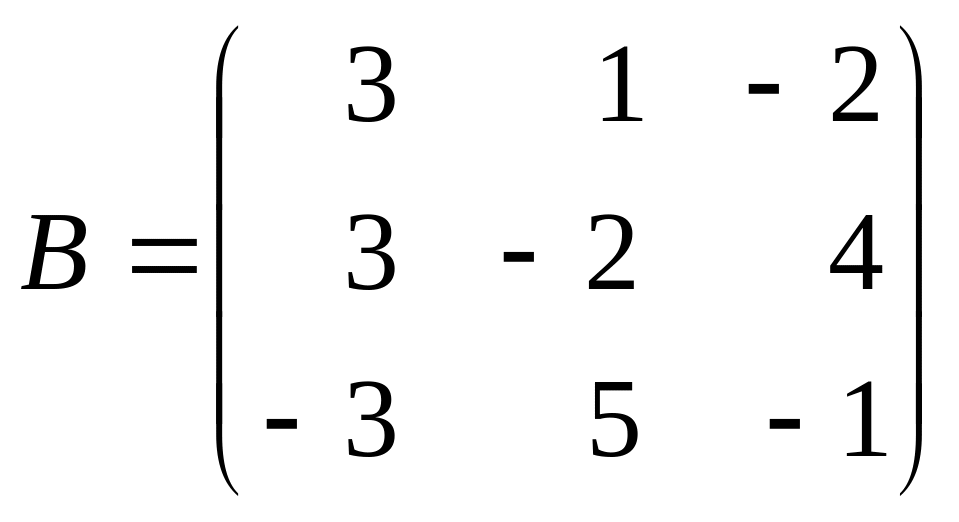