Задача об использовании оборудования
При заданном плане изготовления продукции разного вида на разном оборудовании с заданными производительностями составить план использования оборудования так, чтобы план реализовывался в минимальное время.
Пример.
Производству задано задание по выпуску трех видов продукции в количестве 100, 80 и 60 единиц (тонн, литров и т.п.). Каждый вид продукции может производиться на двух технологических линиях А и В. Производительность линий задается в виде следующей таблицы:
-
2
5
6
3
4
8
Число 3 в таблице показывает время, необходимое для изготовления на линии В одной единицы продукции первого вида. Составить план использования оборудования так, чтобы задание выполнялось в кратчайшее время.
В
качестве неизвестных в построении
математической модели примем двухиндексную
переменную
– количество продукции вида j,
которое следует изготовить на линии
i.
Переменная
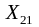соответствует
объему производства линии В при
производстве продукции первого вида.
Время работы линии А составляет
,
а линии В
.
При этом, условия выполнения плана по номенклатуре представляются как
.
Все
переменные неотрицательные:
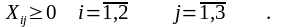
Поскольку линии работают одновременно, время T одной из возможных реализаций задания определяется по худшему времени по всем линиям:
.
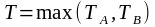Среди всех возможных значений в задаче требуется определить минимальное. Таким образом, имеем функцию цели:
.
Такая линейная задача называется минимаксной.
Итак, мы рассмотрели простейшие в смысле постановки задачи экономики, планирования и управления и соответствующие им модели линейного программирования. Естественно, что рассмотренные задачи далеко не исчерпывают всех типов задач этой области. Существует большой класс так называемых линейных экономико-математических моделей (например, межотраслевые модели, модели отношений субъектов и т.п.), сложных по пониманию даже на этапе постановка задачи. Их исследование – предмет других учебных курсов. Однако при анализе таких проблем непременно, так или иначе, используется линейное программирование. Кроме того, мы вовсе не рассматривали моделей линейного программирования в инженерных задачах.
Заметим также, что, если модель содержит линейные функции, но переменные должны быть целыми или дискретными, то задача становится нелинейной, а ее решение сложнее решения задачи линейного программирования.