Задача математического программирования
Задача математического программирования имеет следующий
(1)
(2)
,
Задача формулируется следующим образом.
Найти n компонентов вектора x,
чтобы достигался максимум или минимум
функции цели
(1) при выполнении m ограничений
в виде равенств или нестрогих неравенств.
Вектор x называется допустимым, если он удовлетворяет всем ограничениям (2).Если хотя бы одно из ограничений (2) не выполняется, то вектор недопустим. При этом, x должно быть из множества X , в качестве которого можно задавать любые действительные числа, целочисленные значения, дискретные и т.п. По умолчанию X – множество действительных чисел.
Множество допустимых точек образует
область допустимых значений D задачи
математического программирования (1)
– (2). Таким образом, если x*-
допустимая точка, то x*
D
. В реальных задачах принятия решений
экономики, планирования и управления
с моделями математического программирования
чаще всего бывает бесконечное множество
допустимых точек.
В задаче
D
:
(3)
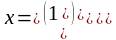– допустимое решение (точка, вектор).
Точка
–
называется оптимальной точкой
(оптимальным решением или просто
решением), если она:
а) допустима (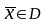
);
б) в задаче на максимум она удовлетворяет соотношению
,
(
);
в задаче на максимум она удовлетворяет соотношению
,
(
).
Оптимальных точек может быть конечное число (1,2,…n) или бесконечное число. Так, в представленной выше задаче (3) существует единственное оптимальное решение
.
Замечания. Следует еще раз заметить, что точка (решение, вектор) является либо оптимальной, либо не оптимальной. Другого определения не существует. Не бывает «почти оптимального» решения или «самой оптимальной» точки. Также не существует «почти допустимых» точек или решений, «близких» к допустимому. К сожалению, такие характеристики можно еще услышать, хотя и в ненаучных кругах.
Варианты идкз № 1 Построить математическую модель.
Вариант 1.
Предприятие может выпустить четыре вида продуктов, измеряемых в граммах, килограммах, центнерах и тоннах. Продукты реализуются по ценам 12, 13, 15, 16 денежных рублей за единицу каждого из продуктов. Продукция выпускается из трех видов ресурсов, запасы которых равны, соответственно, 48 тысяч литров, 160 метров и 250 тысяч часов. Затраты каждого вида ресурса (строка) на производство единицы каждого продукта (столбец) определяются таблицей:
-
1
2
1
3
6
5
5
4
7
9
8
11
Требуется определить план выпуска продукции, при котором суммарный доход от продажи будет максимальным.
Вариант 2.
Нефтеперерабатывающий завод должен ежеквартально поставлять, соответственно, 30, 20, 30 и 30 единиц некоего нефтепродукта. Возможности производства в каждом квартале равны 10, 30, 20 и 50 единиц нефтепродукта. Стоимость производства единицы нефтепродукта в пределах возможностей квартала равна 12 денежным единицам. Стоимость хранения за один квартал одной единицы нефтепродукта составляет 5 денежных единиц. Стоимость дополнительного производства одной единицы нефтепродукта равна 17 денежных единиц. При этом используются ресурсы следующих кварталов, что сокращает возможности выпуска в нем. Определить объемы ежеквартального выпуска и хранения нефтепродукта, чтобы суммарные затраты были минимальными.
Вариант 3.
Имеются 3 поставщика нефтепродукта с запасами его 350, 270 и 120 единиц. Пусть имеются 4 потребителя нефтепродукта, которым требуется не менее 300, 350, 60 и 20 его единиц. Затраты на перевозку одной единицы нефтепродукта от каждого поставщика (строка) каждому потребителю (столбец) определяются следующей таблицей:
-
84
75
83
86
15
18
17
13
200
197
201
205
Определить такой план перевозки нефтепродукта от каждого поставщика к каждому потребителям, чтобы достигался минимум суммарных затрат на перевозку продукции.
Вариант 4.
Нефтеперерабатывающий завод выпускает 3 сорта бензина I, II, III и продает их по ценам, соответственно, 800, 900 и 1000 денежных единиц за тонну. Бензины получаются смешиванием четырех веществ: алкилата, крекинг-бензина, бензина прямой перегонки и изопентана. Запасы этих веществ равны 540, 425, 335 и 210 тонн. Пропорция смешивания бензина I: 1:3:4:2 , бензина II: 2:1:3:1 , а бензина III: 1:2:3:3 . Определить план выпуска бензинов, при котором достигается максимум суммарного дохода от их продажи.
Вариант 5.
Газодобывающему предприятию требуется отремонтировать 15 газовых скважин. В наличии имеется 5 ремонтных бригад. Первая бригада может отремонтировать 5 скважин, вторая и третья по 4, четвертая 3, пятая 2. Затраты в денежных единицах на ремонт каждой бригадой (строка) каждой скважины (столбец) определяются следующей таблицей:
4 |
11 |
25 |
38 |
69 |
46 |
50 |
97 |
63 |
43 |
77 |
83 |
9 |
21 |
16 |
3 |
14 |
23 |
37 |
68 |
46 |
52 |
95 |
65 |
42 |
75 |
81 |
8 |
23 |
19 |
5 |
12 |
22 |
39 |
67 |
44 |
52 |
98 |
65 |
40 |
73 |
80 |
8 |
25 |
18 |
4 |
13 |
24 |
41 |
70 |
43 |
54 |
99 |
64 |
42 |
79 |
84 |
7 |
24 |
17 |
6 |
12 |
25 |
37 |
71 |
45 |
56 |
98 |
69 |
41 |
74 |
83 |
4 |
22 |
19 |
Назначить так бригады на скважины, чтобы суммарные затраты были минимальные.
Вариант 6.
Задача о составе смеси или о питании (все данные условные). Чтобы рационально питаться, студент должен получать в день не менее 100 граммов жира, 50 граммов углеводов и 40 граммов белков. Студент может употреблять в пищу суп, салат, шоколад и пиво, покупаемые по ценам 50,130,120, 70 денежных единиц за килограмм. Содержание трех веществ (столбцы) в килограмме этих четырех продуктов (строки) определяется таблицей:
-
80
40
10
40
70
40
130
110
75
0
80
85
Требуется так составить рацион питания, чтобы суммарные затраты на продукты были минимальными при соблюдении норм содержания веществ.
Вариант 7.
Составить оптимальную производственную программу по критерию минимума суммарных затрат при обработке четырех видов изделий 1,2,3,4 с плановым заданием, соответственно, 200, 100, 150 и 180 штук на трех взаимозаменяемых станках по следующим исходным данным:
|
Ресурсы времени, ч. |
Затраты, руб./шт. |
Произ-ность, шт./ч |
||||||
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
||
I |
63 |
21 |
145 |
25 |
10 |
25 |
43 |
32 |
26 |
II |
84 |
19 |
134 |
29 |
20 |
64 |
102 |
64 |
45 |
II |
126 |
13 |
111 |
26 |
22 |
18 |
32 |
19 |
15 |
Вариант 8.
Составить оптимальный план посева четырех культур (1-4) на трех участках посевной площади (I-III) по следующим исходным данным:
Участки |
Размер посевной площади, га |
Урожайность, ц/га
\Себестоимость, руб./ц 1 2 3 4 |
|||
I |
800 |
200 \ 20 |
70 \ 20 |
70 \ 23 |
30 \ 45 |
II |
700 |
185 \ 25 |
70 \ 25 |
65 \ 12 |
35 \ 42 |
III |
200 |
140 \ 28 |
70 \ 20 |
90 \ 10 |
42 \ 21 |
Вариант 9.
Имеется три сорта взаимозаменяемого нефтесырья в количествах 600, 400, 700 единиц, которое используется при производстве четырех продуктов. Продукты следует произвести в количествах не менее 15, 35, 40 и 90 единиц. В таблице указан расход сырья на единицу продукта:
-
2
3
4
5
6
7
9
8
23
25
24
28
и производственные затраты на единицу продукта в денежных единицах:
-
42
35
20
33
32
27
42
40
27
45
34
35
Определить такой план выпуска продукции из данного сырья, при котором достигается минимум затрат на производство.
Вариант 10.
На трех участках (I-III) поля могут выращиваться три культуры: 1,2,3. В следующей таблице указаны размеры участков в гектарах, урожайность aik (в ц/га) на каждом из участков по каждой культуре, затраты сik в чел.-ч на 1 ц (сik \ aik) и плановое задание по сбору этих культур (в ц):
|
Участки в га |
Урожайность и затраты |
||
|
1 |
2 |
3 |
|
I |
30 |
3\ 15 |
3 \ 15 |
3 \ 16 |
II |
50 |
4 \ 12 |
3 \ 12 |
3 \ 22 |
III |
20 |
2 \ 13 |
2 \ 14 |
3 \ 24 |
|
План |
230 |
250 |
310 |
Определить такую структуру посевов, которая обеспечивает минимальные затраты при выполнении плана.
Вариант 11.
Авиакомпания для организации пассажирских перевозок между центром и четырьмя городами располагает тремя группами самолетов: I группа из 15 четырехмоторных самолетов, II – из 27 двухмоторных и III группа – из 30 двухмоторных старого образца.
Количество пассажиров в тыс. человек, перевозимых одним самолетом данного типа по каждому маршруту за 1 месяц, и связанные с этим эксплуатационные расходы на 1 самолет в тыс. руб. указаны, соответственно, как числитель и знаменатель дроби. Кроме того, заданы количество пассажиров, которое необходимо перевезти по данному маршруту в месяц, и стоимость одного билета.
Самолет |
Города |
|||
1 |
2 |
3 |
4 |
|
I |
20/2 |
20 /2 |
15/3 |
- |
II |
30 /3 |
25 / 3 |
20/2 |
25 /2 |
III |
25 /1 |
- |
15/1 |
16 /2 |
Количество пассажиров, тыс. чел. |
60 |
40 |
35 |
30 |
Стоимость билета |
2500 |
1500 |
2000 |
1500 |
Распределить самолеты по маршрутам так, чтобы прибыль авиакомпании была максимальной.
Вариант 12.
Три предприятия (I, II, III) могут обеспечить на каждом выпуск трех видов изделий (А, Б, В). Основные производственно-экономические данные приведены в следующей таблице. Составить оптимальный годовой план загрузки предприятий из условий получения максимального числа комплектов, в каждый из которых изделия входят в отношении 4:2:3.
-
Месячная производительность, шт.
Себестоимость, руб./шт.
А
Б
В
А
Б
В
I
10
30
40
12
18
20
II
30
20
30
14
16
19
III
20
10
20
11
115
18
Вариант 13.
Построить модель задачи Варианта 12 при условии, что каждое предприятие выпускается изделие только одного вида.
Вариант 14.
При составлении суточного рациона кормления некоторых животных можно использовать сено (не более 150 кг) и силос (не более 200 кг). рацион должен обладать определенной питательностью: число кормовых единиц не менее 50, содержать белка не менее 2 кг, кальция не менее 200 г и фосфора не менее 100 г. в следующей таблице приведены данные о содержании указанных компонентов в 1 кг каждого продукта и стоимость продуктов в денежных единицах за килограмм:
Продукты |
Количество кормовых единиц/кг |
Белок, г/кг |
Кальций, г/кг |
Фосфор, г/кг |
Стои- мость
|
Сено |
0,8 |
70 |
1,5 |
3 |
2 |
Силос |
0,35 |
30 |
2,5 |
2 |
1 |
Определить такой рацион питания животных, чтобы суммарная стоимость продуктов была минимальной.
Вариант 15.
Из четырех видов материалов (1-4) составляют три вида сплавов ( I-III). Цены единицы каждого материала равны 3, 4,5 и 1 денежных единиц. Сплавы продаются по ценам, соответственно, 100 , 300 , 400 денежных единицы за единицу веса. Сплав II должен содержать не менее 15% материала 2, не менее 20% материала 1 и не более 10% материала 4. Сплав III должен содержать не менее 25% материала 1, не менее 20% материала 4 и не более 10% материала 2. За некоторый срок предприятие может выпускать не более 100 единиц веса сплава I, не более 50 единиц веса сплава II, не более 30 единиц веса сплава III.
Найти производственный план, обеспечивающий предприятию максимальный доход от продажи сплавов.
Вариант 16.
Предприятие может выпускать продукцию по трем способам производства. При этом за 1 час по 1-му способу производства оно может выпустить не более 50 единиц продукции, по 2-му – 70 единиц и по 3-му – 80 единиц продукции. Расход и запасы производственных ресурсов за час при различных способах производства представлены в следующей таблице:
Ресурсы
|
Сырье |
Стан. парк |
Рабоч. сила |
Энергия |
Транс. расходы |
Прочие расходы |
1 |
20 |
1 |
17 |
21 |
101 |
4 |
2 |
17 |
2 |
13 |
11 |
100 |
3 |
3 |
26 |
4 |
14 |
31 |
100 |
2 |
Запасы |
100 |
70 |
170 |
500 |
4000 |
70 |
Определить план выпуска продукции по каждому способу производства по критерию максимума выпуска продукции за 42 часа.
Вариант 17.
Обработка деталей А, Б и С может производится на трех станках (I, II, III). В следующей таблице указаны нормы затраты времени на обработку станком соответствующей детали, продажная цена детали в денежных единицах, оплата одного часа работы станка и предельное время работы станка.
Станки |
Нормы времени |
Оплата |
Время работы станка |
||
А |
Б |
С |
|||
I |
2 |
1 |
1 |
5 |
42 |
II |
6 |
3 |
2 |
2 |
61 |
III |
2 |
1 |
4 |
3 |
21 |
Цена |
30 |
40 |
35 |
|
|
Предполагая, что любая деталь может производиться на любом из станков, определить план выпуска продукции, при котором достигается максимум дохода от продажи.
Вариант 18.
Решить задачу Варианта 17 из условия, что деталь каждого вида изготавливается только на одном станке.
Вариант 19.
Для перевозки пассажиров на некотором маршруте используются пассажирские и скорые поезда. в таблице указан наличный парк вагонов разных типов, из которых ежедневно можно комплектовать поезда и количество пассажиров, вмещающихся в каждом из вагонов:
|
Вагоны |
||||
Багажный |
Почтовый |
Плацк. |
Купейный |
Мягкий |
|
Скорый |
1 |
1 |
8 |
5 |
2 |
Пассажирский |
1 |
- |
9 |
5 |
1 |
Число пассаж. |
- |
- |
54 |
36 |
18 |
Парк вагонов |
20 |
18 |
100 |
80 |
65 |
Определить оптимальное число скорых и пассажирских поездов, при котором число перевозимых пассажиров достигает максимума.
Вариант 20.
Для нарезки труб трех размеров 50 метров, 150 метров и 200 метров в комплекте 2:3:1 разрезают 150 труб по 250 метров и 100 труб по 150 метров. Определить план раскроя по критерию минимума обрезков труб при выполнении условия комплектности.
Следующие варианты соответствуют номеру задачи по задачнику
Калихман И.Л. Сборник задач по математическому программированию, М.,
Высшая школа, 1975, 271с.
Вариант |
21. |
Вариант |
22. |
Вариант |
23. |
174 |
|
175 |
|
176 |
|
|
|
|
|
|
|
Вариант |
24. |
Вариант |
25. |
Вариант |
26. |
178 |
|
179 |
|
180 |
|
|
|
|
|
|
|
Вариант |
27. |
Вариант |
28. |
Вариант |
29. |
181 |
|
182 |
|
183 |
|
|
|
|
|
|
|
Вариант |
30. |
Вариант |
31. |
Вариант |
32. |
184 |
|
185 |
|
195 |
|
|
|
|
|
|
|
Вариант |
33. |
Вариант |
34. |
Вариант |
35. |
196 |
|
197 |
|
198 |
|
|
|
|
|
|
|
Вариант |
36. |
|
|
|
|
199 |
|
|
|
|
|