7.3.6. Диференційна ланка.

Вихідна величина Y диференційної ланки пропорційна до швидкості зміни її вхідної величини Х. Це функціональна залежність так званої ідеальної диференційної ланки:

Y = K .

На практиці застосовуються реальні диференційні ланки, які описуються рівнянням:

K , де

K- коефіцієнт підсилення диференційної ланки,

- стала часу диференціювання.

Електричним аналогом диференційної ланки є такий RC ланцюг:

При стрибкоподібному сигналі Uвх виникає перехідний процес, що характеризується такими струмами: , .

При = RC

або _вих. (t) = RC _вх (t)

Позначимо RC = T; U_вих = Y ; U_вх = Х, тоді отримаємо

Т Y^І (t) + Y (t) = Т Х^І (t) .

В загальному вигляді диференційна ланка описується рівнянням:

Т Y^І (t) + Y (t) = К Т Х^І (t)

Оскільки зміна Y (t) залежить від похідної Х^І (t) вхідного сигналу ,то така ланка називається диференційною. При стрибкоподібному збуренні Х(t) на вході вихідна величина

Y (t) = , де - стала часу диференціювання, яка визначається, як дотична до кривої Y (t) в точці Y (0). Передавальна функція диференційної ланки має вигляд: , а її амплітудно-фазова характеристика – , де K = .

Графічно частотні характеристики диференційної ланки мають такий вигляд:

АЧХ і ФАХ АФХ

Диференційна ланка є фазовипереджуючою, тобто гармонійні коливання вихідної величини Y(t) випереджують на час ∆t коливання її вхідної величини Х (t):

7.4. З’єднання ланок.

Всі складні комбінації промислових САР утворюються з допомогою лише трьох типів зєднань: паралельного, послідовного та зустрічно – паралельного. При визначенні сумарних або результуючих характеристик складних динамічних систем застосовується принцип суперпозиції або накладання (алгебраїчної суми). При цьому найбільш зручно користуватися операторною та векторною (частотною) формами подання динамічних властивостей ланок.

7.4.1. Паралельне з’єднання ланок.

Розглянемо систему, яка складається з двох паралельно з’єднаних односторонньо спрямованих ланок:

Для такої системи, враховуючи принцип суперпозицій, справедливо: 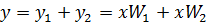, де 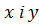- векторна форма запису відповідно вхідної та вихідної величин, W1 і W2 – вектори АФХ.

Тоді передавальна функція такої системи:

Результуючий вектор W_р визначається за правилом складання векторів при певній частоті ω₁. W_p = = ( ) + ί ( ).

Правило: При паралельному з’єднанні n ланок результуюча передавальна функція Wр і результуюча АФХ W(ίω) системи утворюються шляхом додавання передавальних функцій і АФХ окремих ланок.