Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

«Брянский государственный инженерно-технологический университет»

Кафедра математики

Методические указания и задания к выполнению

расчетно-графической работы по теме:

"Приближенные методы решения

дифференциальных уравнений"

для студентов всех специальностей и всех направлений подготовки бакалавров очной формы обучения

Брянск 2015

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

«Брянский государственный инженерно-технологический университет»

Кафедра математики

УТВЕРЖДЕНЫ

научно-методическим

советом университета

Протокол № ____

oт “____”___________2015 г.

Методические указания и задания к выполнению

расчетно-графической работы по теме:

"Приближенные методы решения

дифференциальных уравнений"

для студентов всех специальностей и всех направлений подготовки бакалавров очной формы обучения

Брянск 2015

Составители: доцент Камозина О.В.,

доцент Котова И.А.

Рецензент:

профессор кафедры «Физика», д. ф.-м. н. Евтюхов К.Н.

Рекомендованы редакционно-издательской и методической комиссиями механико-технологического факультета БГИТУ.

Протокол № 1 от 10.09.2015 г.

Приближенные методы решения дифференциальных уравнений

Решение многих дифференциальных уравнений нельзя свести к интегрированию известных функций. Поэтому важное значение приобретают приближенные методы решения.

Существуют два метода численного решения дифференциальных уравнений 1-го порядка: метод Эйлера и метод Рунге-Кутта.

1. Метод Эйлера

Для данного уравнения 1-го порядка

(1)

можно составить таблицу приближенных значений частного решения, удовлетворяющего начальному условию

(2)

или приближенно вычертить интегральную кривую на некотором отрезке[ ].

По методу Эйлера данный отрезок [ ] разбивается точками на n частичных отрезков.

На первом частичном отрезке [ ] искомая интегральная кривая, проходящая через известную точку M₀( ) заменяется касательной к ней в точке

^,

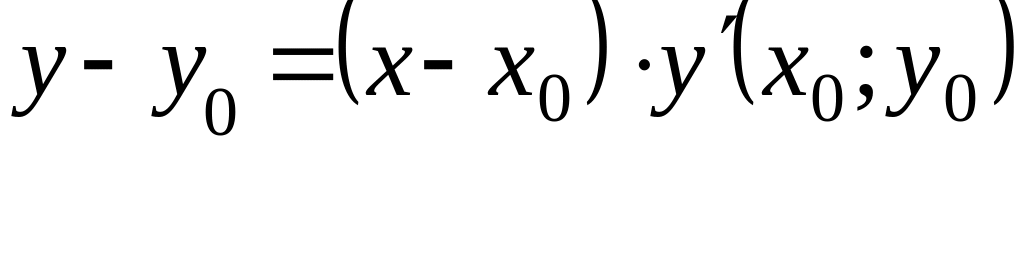Откуда при получается приближенное значение искомого решения уравнения в точке

.

Далее тем же способом для отрезка [ ] находим приближенное значение искомого решения в точке

.

Продолжая этот процесс, последовательно находим приближенные значения искомого решения в точках .

С увеличением , при достаточно малой длине частичных отрезков, этим методом можно достигнуть заданной точности решения.

Данный отрезок [ ] удобно разделить на частичные отрезки одинаковой длины

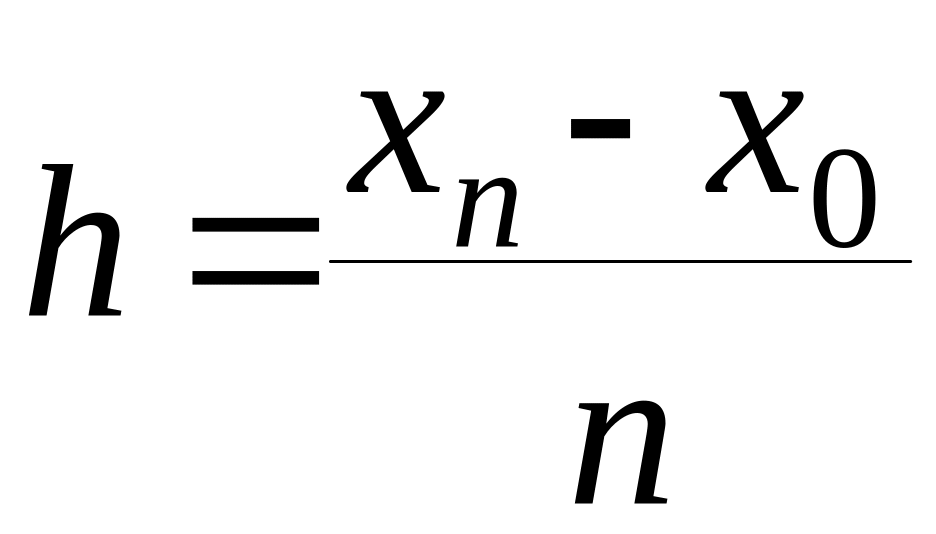(шаг).

Тогда все последовательные приближенные значения решения уравнения (1), удовлетворяющего начальному условию (2), вычисляются по рекуррентной формуле

.

Таким образом, по методу Эйлера интегральную кривую, проходящую через точку , заменяют ломаной (ломаной Эйлера), каждый отрезок которой проведен по направлению поля, определенного уравнением (1). Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведенной через начальную точку каждого отрезка.

Недостатки метода Эйлера:

1. Малая точность при значительном шаге и большой объем работ при малом шаге.

2. Систематическое накопление ошибок.

Поэтому метод Эйлера применяют лишь для грубых приближений.

Расчет ведется по следующей схеме:

0
1
2
…	…	…	…	…
-1