VII. Расчет сваи-оболочки

Рассчитываем сваю-оболочку среднего ряда, так как она наиболее нагружена. Расчетное сечение расположено вверху сваи-оболочки.

1. Внутренние усилия в свае-оболочке среднего ряда.

• вверху

M_b  1323,1 кНм _,

Q  89,295 кН _,

N_b  5653,3 кН _,

эксцентриситет

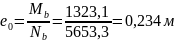
2. Исходные данные по материалам.

Расчетные характеристики для бетона класса В30 сваи-оболочки

принимаем по табл. 5:

R_b  17МПа ,

^Rb,ser

 22МПа

^Rbt

 1,2МПа ,

E_b  43000МПа . Коэффициент условий работы бетона

Расчетные характеристики арматурных сталей:

 _b  1,1.

		- напрягаемая	арматура в свае-оболочке		класса A-IV ( Rs  510МПа ,
Rs ,ser	 590МПа , Rsc		 400МПа , Rsw	 405МПа ,	Eb	 190000МПа ),

- спирали – ненапрягаемая класса A-I

Расчет прочности кольцевого сечения

1. Предварительное напряжение арматуры с учетом всех потерь.

Максимально допустимое значение предварительного напряжения в арматуре класса A-IV без учета потерь равно

σ_sp,0 = 0,9R_s,n = 0,9 ·590 = 531 МПа.

Полные потери не должны быть меньше 100 МПа, поэтому принимаем полные потери

Δσ_sp= 100 МПа.

Предварительное напряжение арматуры с учетом всех потерь

σ_sp = σ_sp,0 - 100 МПа = 531 – 100 = 431 МПа.

2. Геометрические характеристики сваи-оболочки, определенные ранее.

Наружный диаметр

d₁  1,6 м .

Толщина стенки   0,2 м .

Отношение внутреннего диаметра сваи-оболочки к наружному

Площадь сечения сваи-оболочки

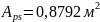
Момент инерции поперечного сечения сваи-оболочки

_,

Приведенная длина стойки

3. В качестве продольной напрягаемой арматуры принимаем арматуру Ø25 A-IV независимо от диаметра оболочки. Площадь поперечного сечения одного стержня Ø25

4. Процент армирования сваи-оболочки из преднапряжённого железобетона

  1,5%

5. Количество продольных напрягаемых стержней

4

Окончательно принимаем продольную арматуру – 27 стерженей Ø25 A-IV с общей площадью

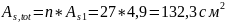
6. Коэффициент приведения

7. Приведенная площадь сечения сваи-оболочки:

8. Диаметр окружности, проходящей через центр тяжести напрягаемых стержней:

Где d₁  160см наружный диаметр сваи-оболочки,

a_p  5см - защитный слой продольной арматуры,

d  2,5см - диаметр продольной арматуры.

Продольную напрягаемую арматуру ставим по окружности диаметром d_s= 1,475 м.

9. Погонная интенсивность продольной арматуры:

10. Приведенный момент инерции сваи-оболочки:

11. Радиус инерции приведенного сечения:

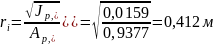12. Гибкость элемента:

Следовательно, расчет ведем с учетом продольного прогиба сваи.

13. Критическая сила:

• При вычисляется по формуле

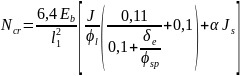
Коэффициент, учитывающий влияние предварительного напряжения арматуры на жесткость элемента. При равномерном обжатии сечения напрягаемой арматурой

Где

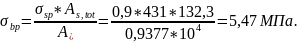
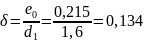
Так как , принимаем   0,134 ,

_l  2

- коэффициент, учитывающий влияние длительно действующей

нагрузки на прогиб элемента

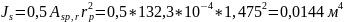
При 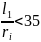критическая сила вычисляется по формуле

Коэффициент, учитывающий влияние продольного изгиба

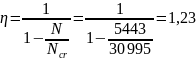
14. Расчет внецентренно сжатых элементов кольцевого сечения при соотношении внутреннего и наружного радиусов r₁/r_i > 0,5 с арматурой, равномерно распределенной по длине окружности (при продольных стержнях не менее 7), производится из условия

15. Вычисляем значение относительного угла, ограничивающего сжатую зону кольцевого сечения:

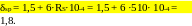
16. Напряжение в рабочей арматуре сваи-оболочки с учетом коэффициента γ_s6=1,1 (для арматуры класса A-IV):

σ_sp = 1,1·431 = 474 (МПа).

17. Величина относительной площади сжатой зоны бетона вычисляется по формуле:

18. Вычисляем коэффициенты:

,

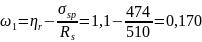
где η_r = 1,1 ( для арматуры класса A-IV);

19. Величина относительной площади сжатой зоны бетона вычисляется по формуле:

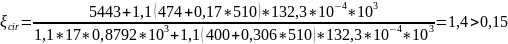Значение ξ_cir оставляем без изменения. Если ξ_cir < 0,15, то относительную площадь сжатой зоны бетона определяем по формуле:

20. Определяем несущую способность сечения. Для этого вычисляем Z_s (расстояние от равнодействующей в напрягаемой арматуре до центра тяжести приведенного сечения):

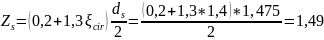
но принимаем его не более d_s/2.

Так как ,

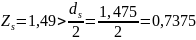Принимаем _.

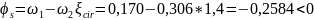
Проверяем прочность нормального сечения:

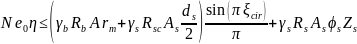
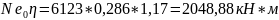
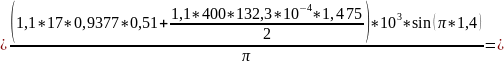
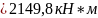
Проверяем прочность нормального сечения:

Условие выполняется, следовательно, прочность по нормальному сечению обеспечена.