
- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •Орел 2016
- •Рецензент:
- •Орлова и.В.
- •Содержание
- •Предисловие
- •Введение. Понятие, роль и этапы математического моделирования в экономике и финансах
- •Раздел1. Основы линейного программирования
- •1.1. Экономико-математическая модель оптимизационной задачи и задачи линейного программирования
- •1.2. Графический метод решения задачи линейного программирования
- •1.3. Симплекс-метод решения задач линейного программирования
- •1.4. Основы теории двойственности
- •Задачи для самостоятельного решения
- •Раздел 2. Специальные задачи линейного программирования
- •2.1. Задачи дискретного программирования
- •2.2.Транспортная задача. Методы построения опорного плана. Улучшение плана методом потенциалов
- •2 Этап.Построение системы потенциалов и проверка начального плана на оптимальность
- •Задачи для самостоятельного решения
- •Раздел 3. Задачи многокритериальной оптимизации
- •3.1. Происхождение и постановка задачи многокритериальной оптимизации
- •3.2. Основные методы решения многокритериальных задач
- •Задачи для самостоятельного решения
- •Раздел 4. Неотрицательные матрицы и модели Леонтьева
- •4.1. Некоторые сведения из линейной алгебры Собственные значения и собственные векторы неотрицательных матриц
- •Теорема Фробениуса – Перрона. Число и вектор Фробениуса, их свойства
- •4.2. Модель Леонтьева6 многоотраслевой экономики
- •Задачи для самостоятельного решения
- •Рекомендуемая литература
- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •7,75Усл. Печ. Л. Тираж 500 экз. Заказ № 225
1.4. Основы теории двойственности
С каждой задачей линейного программирования
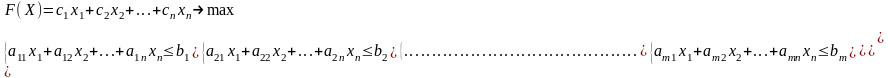
тесно связанадругая линейная задача, называемая двойственной или сопряженнойпо отношению к прямой задаче

Теория двойственности оказалась полезной для многовариантного анализа оптимальных решений задач линейного программирования.
Внимательное рассмотрение модели двойственной задачи позволяет увидеть правила ее составления:
1) если целевая функция исходной задачи формулируется намаксимум, то целевая функция двойственной задачи — на минимум(и наоборот), при этом в задаче на максимум все неравенства в функциональных ограничениях со знаками« », в задаче на минимум — со знаками « »;
2) матрица коэффициентов при неизвестныхв системе ограничений двойственной задачи получается транспонированием соответствующей матрицы в системе исходной задачи;
3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений всистеме двойственной задачи — числу переменных в исходной;
4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограниченийисходной задачи, а правыми частями в ограничениях двойственнойзадачи — коэффициенты при неизвестных в целевой функции исходной;
5) каждому ограничению одной задачи соответствует переменнаядругой задачи, номер переменной совпадает с номером ограничения.
Переменные
двойственной задачи yiв
экономической литературе получили
различные названия: теневые цены,объективно
обусловленные оценки, двойственные
оценки (илицены) ресурсов. Смысл этих
названий состоит в том, что это условные,
«ненастоящие»
цены. В отличие от «внешних» цен
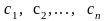 на продукцию, известных, как правило,
до начала производства, цены ресурсов
на продукцию, известных, как правило,
до начала производства, цены ресурсов
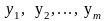 являются
внутренними,
так как они задаются не извне, а
определяются непосредственно в
результате решения задачи, поэтому их
чаще называют оценками
ресурсов.
являются
внутренними,
так как они задаются не извне, а
определяются непосредственно в
результате решения задачи, поэтому их
чаще называют оценками
ресурсов.
Экономическая интерпретация взаимно двойственных задач:
Прямая
задача:
какое количество продукции каждого
вида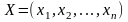 надо произвести, чтобы при заданных
значениях стоимости единицы продукции
сj
(j = 1,…, n),
объемах имеющихся ресурсов bi
(i = 1, m)и
нормах их расходовaijмаксимизировать
выпуск продукции в стоимостном выражении
при условии, что потребление ресурсов
каждого вида не превзойдет имеющихся
запасов.
надо произвести, чтобы при заданных
значениях стоимости единицы продукции
сj
(j = 1,…, n),
объемах имеющихся ресурсов bi
(i = 1, m)и
нормах их расходовaijмаксимизировать
выпуск продукции в стоимостном выражении
при условии, что потребление ресурсов
каждого вида не превзойдет имеющихся
запасов.
Двойственная
задача:
какова должна быть минимальная оценка
единицы каждого из ресурсов
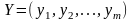 ,
чтобы при заданных величинахbi,
сj,
и aij
минимизировать общую оценку затрат
ресурсов на всю произведенную продукцию
при условии, что затраты на ресурсы при
производстве каждого вида продукции
будут не менее прибыли (выручки) от
реализации этой продукции?
,
чтобы при заданных величинахbi,
сj,
и aij
минимизировать общую оценку затрат
ресурсов на всю произведенную продукцию
при условии, что затраты на ресурсы при
производстве каждого вида продукции
будут не менее прибыли (выручки) от
реализации этой продукции?
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может бытьрешена независимо от другой задачи. Вместе с тем, при решении прямой ЗЛП в «Поиске решений» в Excel формируется «Отчет по устойчивости», в котором содержатся значения двойственных оценок в колонке «Теневая цена» (см. рис. 2). Подробнее с содержанием отчета по устойчивости можно познакомиться в пособии [5].
Связь между оптимальными решениями исходной и двойственной задач может быть установлена на основе теорем двойственности.
MicrosoftExcel 14.0 Отчет об устойчивости |
|
|
|
|||||||||
Лист: [Книга1]Лист1 |
|
|
|
|
||||||||
Отчет создан: 08.07.2016 11:17:58 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
Ячейки переменных |
|
|
|
|
||||||||
|
Ячейка |
Имя |
Окончательное |
Приведенн. |
Целевая функция |
Допустимое |
Допустимое |
|||||
|
|
|
значение |
стоимость |
Коэффициент |
Увеличение |
Уменьшение |
|||||
|
$A$1 |
Х1 |
0 |
-7 |
3 |
7 |
1E+30 |
|||||
|
$B$1 |
Х2 |
30 |
0 |
4 |
8 |
1 |
|||||
|
$C$1 |
Х3 |
10 |
0 |
3 |
1 |
1.75 |
|||||
|
$D$1 |
Х4 |
0 |
-9.666666667 |
1 |
9.666666667 |
1E+30 |
|||||
|
|
|
|
|
|
|
|
|||||
Ограничения |
|
|
|
|
|
|||||||
|
Ячейка |
Имя |
Окончательное |
Теневая |
Ограничение |
Допустимое |
Допустимое |
|||||
|
|
Левая часть |
значение |
цена |
Правая часть |
увеличение |
уменьшение |
|||||
|
$E$4 |
Труд |
80 |
1.333333333 |
80 |
150 |
15 |
|||||
|
$E$5 |
Сырье |
280 |
0 |
480 |
1E+30 |
200 |
|||||
|
$E$6 |
Оборудование |
130 |
0.333333333 |
130 |
30 |
90 |
|||||
Рисунок 2. Отчет по устойчивости
Первая (основная) теорема двойственности. Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:
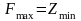 .
.
Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы.
Экономический смысл: план производства продукции
и набор цен (оценок) ресурсов
оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от реализации продукции, найденная при внешних (известных заранее) ценах
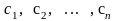
равна затратам на ресурсы по «внутренним» (определяемым только из решения двойственной задачи) ценам
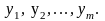
Основная теорема устанавливает также наличие баланса (равенства) между результатами производстваFmaxи совокупными затратами Zminна него.
Вторая
теорема двойственности. Пусть
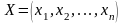 и
и
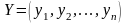 – допустимые решения соответственно
прямой и двойственной задач. Для того,
чтобы они были оптимальными, необходимо
и достаточно, чтобы выполнялись следующие
соотношения
– допустимые решения соответственно
прямой и двойственной задач. Для того,
чтобы они были оптимальными, необходимо
и достаточно, чтобы выполнялись следующие
соотношения
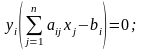 (1)
(1)
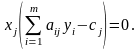 (2)
(2)
Условия (1) и (2) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи (см. пример ниже).
Условия
(1) позволяют определить нулевые
компоненты
оптимального плана двойственной
задачи:если i-ыйресурсостался
после производства (такие ресурсы
называют недефицитными),
то разность в скобке равенства (1) отлична
от нуля, тогда для соблюдения равенства
нулю произведения первый множитель,
т.е.
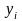 ,
должен быть равен нулю.Таким образом,
двойственные оценки недефицитных
ресурсов равны нулю.
,
должен быть равен нулю.Таким образом,
двойственные оценки недефицитных
ресурсов равны нулю.
Условия
(2) позволяют по известному оптимальному
решению прямой задачи определить
ненулевые
(положительные) компоненты
оптимального плана двойственной
задачи:если
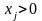 ,
то для соблюдения условий (2) необходимо,
чтобы соответствующие по номеру (j-ые)
ограничения двойственной задачи были
равенствами (уравнениями). Решая
полученную систему уравнений, находим
ненулевые компоненты оптимального
плана двойственной задачи. Следует
заметить, что положительные переменные
двойственной задачи являются оценками
ресурсов, которые израсходованы при
производстве полностью (такие ресурсы
называют дефицитными).
,
то для соблюдения условий (2) необходимо,
чтобы соответствующие по номеру (j-ые)
ограничения двойственной задачи были
равенствами (уравнениями). Решая
полученную систему уравнений, находим
ненулевые компоненты оптимального
плана двойственной задачи. Следует
заметить, что положительные переменные
двойственной задачи являются оценками
ресурсов, которые израсходованы при
производстве полностью (такие ресурсы
называют дефицитными).
Замечания
1. Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находятся с помощью теорем двойственности, называется двойственным симплексным методом. Этот метод выгодно применять, когда первое базисное решение исходной задачи недопустимо или, например, когда число ее ограничений m больше числа переменных n.
2. Глубокая связь между двойственными задачами проявляется также при попытке одновременного решения взаимно-двойственных задач симплекс-методом. При решении одной из задач с помощью симплекс-метода применение соответствующих преобразований к двойственной задаче в учебной литературе также иногда называется двойственным симплекс-методом[2].
Теорема об оценках (третья теорема двойственности).Компоненты оптимального решениядвойственной задачи yi равны значениям частных производных линейнойфункции F по соответствующим аргументамbi, т.е.
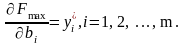
Следствия и уточнения
1) двойственные оценки ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу;
2) двойственные оценки представляют собой оценки влияния свободных членов bi системы ограничений (неравенств) прямой задачи на величину прибыли (выручки) F
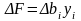 ;
;
3) при изменении запасов недефицитных ресурсов прибыль не изменится, т.к.
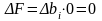 ;
;
4) данная теорема справедлива при незначительных (малых) изменениях запасов ресурсов; эти допустимые изменения определяются интервалами устойчивости двойственных оценок, которые находят специальным образом или в «Отчете по устойчивости» (рис. 2, последние два столбца второй таблицы).
Пример. Сформулировать экономико-математическую модель двойственной задачи к задаче о коврах (см. пункт 1.1).Найти ее оптимальное решение с помощью теорем двойственности. Сделать выводы экономического характера.
Решение:
Исходная задача:
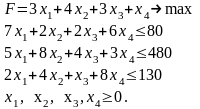
Двойственная задача:
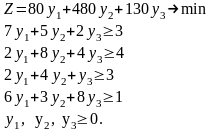
Исходная задача решена в предыдущем разделе. Для решения двойственной задачи воспользуемся второй теоремой двойственности. Подставим оптимальные значения переменных исходной задачи в ее систему ограничений
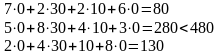
Так
как второе ограничение оказалось
строгим, то, во-первых, второй ресурс
«Сырье» недефицитный (использован при
производстве неполностью), а во-вторых,
согласно условий (1) второй теоремы,
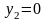 .
.
Остальные две переменные двойственной задачи найдем с помощью условия (2) второй теоремы двойственности.
Так
как в оптимальном плане исходной задачи
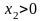 и
и
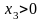 ,
то второе и третье неравенства в системе
ограничений двойственной задачи будут
уравнениями. Решаем систему
,
то второе и третье неравенства в системе
ограничений двойственной задачи будут
уравнениями. Решаем систему
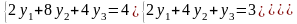
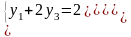
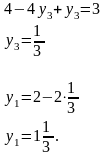
Таким образом, получаем оптимальное решение двойственной задачи, которое совпадает с представленным в отчете по устойчивости (см. рис. 2):
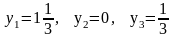 ,
,
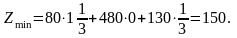
Согласно первой теореме двойственности, оптимальное решение найдено правильно, т.к. .
Экономические выводы:
1.
Так как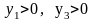 ,
то ресурсы первого и третьего видов
дефицитны. Минимальная цена (оценка) 1
ед. первого ресурса –
,
то ресурсы первого и третьего видов
дефицитны. Минимальная цена (оценка) 1
ед. первого ресурса –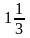 ,
второй ресурс недефицитный (остался
после производства), так как
,
минимальная цена (оценка) 1 ед. третьего
ресурса –
,
второй ресурс недефицитный (остался
после производства), так как
,
минимальная цена (оценка) 1 ед. третьего
ресурса –
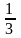 .
.
2. Согласно теореме об оценках, при увеличении запасов 1-го и 2-го ресурсов на 1 ед. общая стоимость продукции увеличится соответственно на усл. ед.и усл.ед., а при увеличении запасов 2-го ресурса на 1 ед. общая стоимость продукции не изменится.
3. Общие затраты на ресурсы по теневым ценам будут минимальны и составят 150 усл. ед.
Материал, изложенный в данном пункте, позволяет определить следующие свойства двойственных оценок (далее ДО) ресурсов:
1. ДО устанавливают баланс(равенство) между результатами производства и совокупными затратами на него. Это свойство вытекает из первой теоремы двойственности.
2. ДО являются характеристикой дефицитности ресурсов (вторая теорема двойственности).
3. ДО выступают, как мера ценности каждой дополнительной единицы ресурса (вторая теорема двойственности).
4. ДО позволяют определить целесообразность включения в план производства новых видов изделий. Это свойство ранее не рассматривалось. Разберем его прямо сейчас.
Пусть
планируется выпуск нового изделия j,
стоимость единицы которого
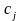 ,
затраты ресурсов на производство единицы
планируемого к производству изделия
соответственно
,
затраты ресурсов на производство единицы
планируемого к производству изделия
соответственно
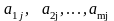 .
Вывод о целесообразности производства
изделия зависит от знака разности
.
Вывод о целесообразности производства
изделия зависит от знака разности
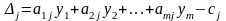 .
.
При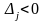 производство выгодно, так как стоимость
превышает затраты ресурсов, при
производство выгодно, так как стоимость
превышает затраты ресурсов, при
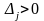 затраты превышают стоимость – производство
невыгодно.
затраты превышают стоимость – производство
невыгодно.
Так, в нашей задаче о коврах выпуск нового вида продукции ценой за единицу 2 тыс. руб. и нормах затрат ресурсов соответственно 5, 2, 9 не будет выгодным, т.к.
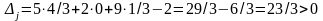 .
.
