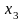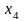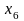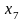1.3. Симплекс-метод решения задач линейного программирования

Универсальным методом решения ЗЛП является симплекс-метод (метод последовательного улучшения решения). Это алгебраический метод, в основе которого лежат преобразования Гаусса системы ограничений модели. Обычно решение задачи симплексным методом проводят с помощью симплексных таблиц.

Выделяют следующие основные этапы симплексного метода:

1) определение какого-либо первоначального допустимого базисного решения задачи;

2) правило перехода к нехудшему решению;

3) проверка оптимальности допустимого базисного решения.

Вначале рассмотримсимплексный метод с естественным базисом. Он применяется, когда первоначальное базисное решение задачи допустимо, то есть не содержит отрицательных компонент.

Пример. Решим симплексным методом задачу о коврах, экономико-математическая модель которой построена в пункте 1.1:

Решение представим в виде последовательности этапов:

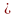1.Систему ограничений стандартной задачи приводим к каноническому виду с помощью дополнительных переменных.Если неравенство знака « », дополнительная переменная берется со знаком «+»; если неравенство знака

« », дополнительная переменная берется со знаком «-»:

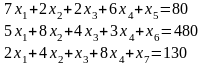
Линейную функцию представим в виде:

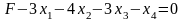².

2. Заполняем первую симплексную таблицу:

Базис	Свободный член	Переменные								Оценочные отношения
	80	7	2	2	6	1	0	0	40
	480	5	8	4	3	0	1	0	60
	130	2	4	1	8	0	0	1	32.5
F	0	-3	-4	-3	-1	0	0	0

Пояснения к последовательности заполнения первой таблицы:

1) процедура заполнения столбца свободных членов и столбцов переменных очевидна;

2) базисными являются те переменные, матрица коэффициентов при которых является единичной подматрицей матрицы системы; в нашей задаче это дополнительные переменные , , ;при выборе основных переменных на первом шаге используют и другие правила, например: в качестве основных переменных на первом шаге следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.

3) последняя строка заполняется коэффициентами целевой функции с противоположными знаками;при этом целевая функция должна быть представлена только через неосновные переменные;

4) в столбце «Свободный член» содержится первоначальное базисное решение задачи, которое получается, если неосновные переменные , , , положить равными нулю.Оно не содержит отрицательных компонент, поэтому является допустимым.Является ли оно оптимальным?

5) для ответа напоставленный вопрос проверяют критерий оптимальности.Критерий оптимальности будет выполнен, если в последней строке симплексной таблицы не будет отрицательных элементов. Если отрицательные элементы присутствуют, то есть неосновные переменные, за счет которых можно увеличить целевую функцию, переведя их в основные. Таким образом, решение задачи продолжается. Самое большое по модулю отрицательное значение определяет разрешающий столбец, следовательно, переменная в следующей симплексной таблице станет базисной.

6) оценочные отношения находят как частное от деления свободных членов на элементы разрешающего столбца 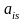, при этом оценочное отношение равно 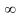, если 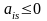. Оценочные отношения – это границы роста переменной разрешающего столбца, при которых сохраняется неотрицательность всех базисных переменных (допустимость решения). Чтобы не нарушалась ни одна из полученных во всех уравнениях границ, нужно рассматривать наименьшее оценочное отношение.Наименьшее оценочное отношение определяет разрешающую строку таблицы. Соответствующая ей переменная выйдет из базиса на следующем этапе решения.

7) на пересечении разрешающих строки и столбца стоит разрешающий элемент – 4.

3. Заполняем вторую симплексную таблицу:

Базис	Свободный член	Переменные							Оценочные отношения
	15	6	0	3/2	2	1	0	-1/2		10
	220	1	0	2	-13	0	1	-2		110
	32,5	1/2	1	1/4	2	0	0	1/4		130
F	130	-1	0	-2	7	0	0	1

Пояснения к последовательности заполнения второй таблицы:

1) вместо переменной в базисе появилась переменная ;

2) в столбцах базисных переменных расставляем нули и единицы: 1 – напротив своей переменной, 0 – напротив чужой; в последней строке против всех основных переменных ставим 0;

3) строка новой основной переменной получается делением всех прежних значений на разрешающий элемент 4;

4) все остальные элементы получаются по правилу прямоугольника, например, элементы столбца свободных членов получены следующим образом:

5) критерий оптимальности не выполнен, определяем разрешающие столбец, строку и элемент.

4. Аналогично заполняем третью симплексную таблицу:

Базис	Свободный член	Переменные							Оценочные отношения
	10	4	0	1	4/3	2/3	0	-1/3
	200	-7	0	0		-4/3	1	14
	30	-1/2	1	0		-1/6	0
F	150	7	0	0		4/3	0	1/3

В последней строке симплексной таблицы нет отрицательных элементов, следовательно, критерий оптимальности достигнут. Оптимальное решение содержится в столбце «Свободный член» и имеет вид

=0

=30

=10

=0

F=150

Экономический смысл полученного решения:

1) производство ковров «Лужайка» и «Дымка» нерентабельно, ковров «Силуэт» целесообразно производить 30 штук, ковров «Детский» – 10 штук;

2) при таком плане производства общая стоимость продукции будет максимальной и составит 150 тыс. рублей;

3) значения дополнительных переменных в оптимальном плане показывают остатки ресурсов после производства; так =200 означает, что ресурс «Сырье» не использован полностью, его осталось 200 кг.

Для решения ЗЛП симплексным методом можно использовать надстройку Excel «Поиск решений» [3], [5].

Замечания:

1. Для использования проведенной процедуры при минимизации линейной функцииF следует искать максимум (-F), затем полученный максимум взять с противоположным знаком. Оптимальное решение будет то же[1].

2.При изучении симплексного метода следует обратить внимание также на его особые случаи (признаки неразрешимости, неединственности оптимального решения, зацикливание) [2], [4].

Понятие о методе искусственного базиса

Если первоначальное базисное решение задачи окажется недопустимым (будет содержать отрицательные компоненты), то применяют модификацию симплексного метода – метод искусственного базиса или М-метод. Он заключается в следующем.

В каждое уравнение, дающее отрицательную компоненту в базисном решении, вводят искусственную переменную , , 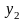…, 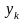с тем же знаком, что и свободный член в правой части. Составляют новую линейную функцию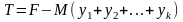 , где M – произвольно большое число, и ищут ее максимум (Т-задача). Выражение называют М-функцией.

Теорема

1. Если в оптимальном решении Т-задачи все искусственные переменные равны нулю, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. , если или минимум М-функции равен нулю).

2. Если имеется оптимальное решение Т-задачи, в котором хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна.

3. Если 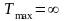, то исходная задача также неразрешима, причем либо , либо условия задачи противоречивы.

Из теоремы следует, что вначаленужно найти минимум М-функции . Если он равен нулю и все искусственные переменные обращаются в нуль, то далее их можно отбросить и решать исходную задачу, исходя из полученного допустимого базисного решения. На практике находят не минимум М-функции, а максимум (-М)-функции.

Пример.Решить следующую ЗЛП методом искусственного базиса

Решение:

1) для получения канонического вида модели введем в систему ограничений дополнительные переменные, которые и будут базисными на первом этапе:

2) получаем первоначальное базисное решение, полагая неосновные переменные и равными нулю – (0,0,-1,3,3); оно недопустимо, так как содержит одну отрицательную компоненту;

3) в первое уравнение, дающее отрицательную компоненту в первоначальном базисном решении, вводим искусственную переменную с тем же знаком, что и свободный член в правой части, и получаем Т-задачу вида

или

Составляем первую симплексную таблицу:

Базис	Свободный член	Переменные						Оценочные отношения
	1	-1	1	-1	0	0	1	1
	3	-1	1	0	1	0	0	3
	3	1	0	0	0	1	0
F	0	-1	-2	0	0	0	0	max
-M	-M	M	-M	M	0	0	0	min

Последняя строка – это (-М)-функция, т.е. (-М ). Заполняем ее, умножая строку на коэффициент (-М), за исключением ячеек, соответствующихбазисным переменным, которые заполняют нулями. Проверяя выполнение критерия оптимальности при отыскании максимума (-М)-функции, определяем, что в последней строке имеется отрицательный элемент во втором столбце; значит, он является разрешающим, переменная переходит в основные. Минимальное оценочное отношение в первой строке, она разрешающая. Переменная переходит в неосновные, обращается в нуль в следующем базисном решении, и далее исключается из рассмотрения.

В соответствии с алгоритмом симплексного метода получаем вторую симплексную таблицу:

Базис	Свободный член	Переменные						Оценочные отношения
	1	-1	1	-1	0	0
	2	0	0	1	1	0
	3	1	0	0	0	1
F	2	-3	0	-2	0	0	max
-M	0	0	0	0	0	0	min

Последняя строка показывает, что критерий оптимальности выполнен:максимум (-М)-функции равен нулю, значит минимум М-функции равен нулю.Далее последнюю строку можно не рассматривать. Получено допустимое базисное решение (0,1,0,2,3), начиная с которого решаем исходную задачу в соответствии с обычным алгоритмом симплексного метода.