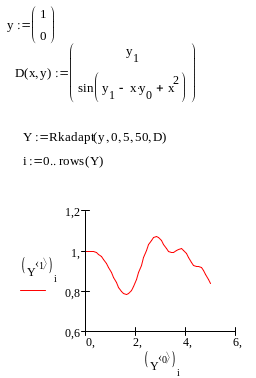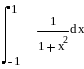Лабораторная работа 4

Цель работы: определение неопределенных и определенных интегралов и производных в программе MathCad с использованием символьных операций,

решение обыкновенных дифференциальных уравнений(ОДУ),

Задание 1

• Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.

• Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.

Таблица – Варианты задания

Номер варианта		Неопределенные интегралы		Определенные интегралы	Производные
1		2		3	4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Примеры

1. Найти неопределенный интеграл .

Результат :

2. Найти определенный интеграл .

Результат .

3. Найти производные первого порядка .

Результат .

4. Найти производные высокого порядка .

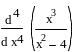Результат

Таблица – Варианты задания

Номер варианта		Неопределенные интегралы		Определенные интегралы	Производные
1		2		3	4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Решение оду

Дифференциальное уравнение первого порядка может по определению содержать помимо самой искомой функции y(t) только ее первую производную y'(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши): у' (t)=f (y(t),t)

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:

Given - ключевое слово;

ОДУ и начальное условие, записанное с помощью логических операторов, причем

начальное условие должно быть в форме y(t₀)=b;

odesolve(t,t₁) - встроенная функция для решения ОДУ относительно переменной t на

интервале (t₀,t₁). Например,

Для того, чтобы визуализировать полученную функцию можно построить ее график:

Обыкновенное дифференциальное уравнение с неизвестной функцией y(t),в которое входят производные этой функции вплоть до y(N) (t), называется ОДУ N-ГО порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функцию y(t) и ее производные от первого до (N-l)-ro порядка включительно. В MathCAD можно решать ОДУ высших порядков как с помощью вычислительного блока Given/odesolve, так и путем сведения их к системам уравнений первого порядка. Внутри вычислительного блока:

- ОДУ должно быть линейно относительно старшей производной, т. е. фактически должно быть поставлено в стандартной форме;

- начальные условия должны иметь форму y(t)=b или у' (t)=b

Например,

Решение систем дифференциальных уравнений.

Систему дифференциальных уравнений можно решить используя тот же блок Given/odesolve . При этом количество начальных условий равно сумме порядков всех уравнений, входящих в систему.

Например:

1. Решение дифференциальных уравнений без помощи блока решений.

MathCAD содержит следующие встроенные функции для решения дифференциальных уравнений:

• rkfixed – метод Рунге-Кутта с фиксированным шагом интегрирования;

• Rkadapt – метод Рунге-Кутта с переменным шагом интегрирования (величина шага адаптируется к скорости изменения функции решения);

Эти функции имеют сходные параметры (y, a, b, n, D):

• y – вектор начальных значений неизвестных функций, входящих в систему (в случае одного уравнений и одной неизвестной функции – это просто число);

• a – начало отрезка, на котором ищется решение (именно в этой точке находятся значения вектора y);

• b – конец отрезка интегрирования;

• n – количество частей, на которые разбивается отрезок интегрирования;

• D(x, y) – векторная функция, элементы которой содержат правые части уравнений системы в нормальной записи (когда левые части – производные от соответствующих функций, а в правых частях производные отсутствуют)

Например: