Глава 19 методы постоянного тока

19.1. Поле постоянного электрического тока

Свойства электромагнитного поля, как и свойства сейсмического, гравитационного или магнитного полей, удобно характеризовать некоторой функцией - потенциалом электрического поля U. Потенциал постоянного электрического поля постоянен во времени и является только функцией координат х, у, z точек среды, поэтому он представлен скалярной величиной, связанной с напряженностью поля Е.

(19.1)

Модуль равен расстоянию от начала координат до точки, где определяется потенциал. Напряженность постоянного электрического поля - вектор с компонентами по осям координат Е_х, Е_у и Е_z.

По электрическим свойствам горные породы можно разделить на проводники и изоляторы. Величина протекающего в проводнике тока определяется законом Ома:

(19.2)

где I - сила тока в проводнике; R - сопротивление проводника; U₁ и U₂ - значения потенциала электрического поля на концах проводника. В свою очередь, сопротивление проводника

(19.3)

где 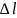- длина проводника; S — площадь его поперечного сечения; - удельное электрическое сопротивление проводника, характеризующее его электрические свойства.

Нормальное поле точечного источника. Поле постоянного электрического тока в однородном проводящем полупространстве (при ) называют нормальным электрическим полем постоянного тока.

В однородной среде при точечном источнике А на поверхности (второй источник отнесен в бесконечность) ток I течет во все стороны равномерно (рис. 19.1, а). Поверхности равного потенциала (эквипотенциальные поверхности) U перпендикулярны прямым токовым линиям, т.е. являются полусферами с центром в точке А. Разность потенциалов между двумя точками М и N на поверхности или между двумя эквипотенциальными поверхно­стями, проходящими через эти точки, может быть представлена согласно формулам (19.2) и (19.3) в виде

(19.4)

Поскольку , а поперечное сечение поверхности полусферы при больших AM и AN по сравнению с MN, то

(19.5)

Эта формула позволяет определить разность потенциалов при известном токе, удельном сопротивлении породы, расстояниях между точками наблюдений М и N и источником. И наоборот, измерив и и зная расстояние между электродами, вычислить удельное сопротивление пород. Допустив, что получаем оценку потенциала U точечного источника, т.е. разность потенциалов между точкой измерения и бесконечностью (при )

(19.6)

Рис. 19.1. Нормальное поле поверхностного точечного (а) и двухточечного (б) источника в однородной изотропной среде. Линии: 1 - эквипотенциальные; 2 - токовые

Заметим, что на практике в качестве источника служит электрод любой формы, размеры заземленной части которого должны быть в несколько раз меньше расстояний, используемых при изучении поля. Это условие выполняется во всех случаях, поэтому формулы расчета для точечного источника применимы в практической электроразведке.

Исходя из формулы (18.3), получим, что напряженность нормального электрического поля, созданного точечным электродом, и плотность тока будут соответственно равны

(19.7)

Установки для измерения сопротивлений. Нормальные поля постоянных электрических токов могут изучаться разными установками, т.е. при разных сочетаниях питающих (АВ) и приемных (MN) электродов. Согласно формуле (19.6) для двухэлек- тродной установки AM ( ).

(19.8)

При трехэлектродной установке ( ) удельное электрическое сопротивление можно оценить по формуле

(19.9)

В электроразведке обычно применяют симметричные четырехэлектродные установки AMNB (рис. 19.1, б). Один питающий электрод (например, А) - положительный, другой (В) - отрицательный. Разность потенциалов на приемных электродах (MN) от электрода А определяют по полученной выше формуле (19.5), аналогичным образом можно получить разность потенциалов от отрицательного электрода В, путем замены А на В и I на -I. Разность потенциалов в точках M и N от обоих электродов АВ равна сумме :

(19.10)

Из этой формулы следует, что если измерены разность потенциалов между приемными электродами и сила тока I в питающей линии АВ, а также определены расстояния между электродами, то можно вычислить удельное электрическое сопротивление однородной среды, как

(19.11)

где

- коэффициент геометрии установки, зависящий от расстояния между электродами.

Для измерения сопротивлений применяют и другие установки, например, при глубинных исследованиях используют так называемые дипольные установки (рис. 19.2). Если приемный диполь перпендикулярен к радиусу r между его центром и центром питающего диполя АВ, а угол α между радиусом и питающей линией АВ находится в пределах , то такую установку называют азимутальной. Частным случаем азимутальной ( ) является экваториальная установка . Если приемный диполь ( ) направлен вдоль r, а , то такую установку называют радиальной. Частным случаем ради­альной установки ( ) является осевая ( ) установка.

При работах дипольными установками величина ρ вычисляется также по формуле (19.11), однако множитель К, связанный с геометрией установки, имеет вид

(19.12)

где q - коэффициент близкий к единице и зависящий от вида дипольной установки.

Распределение плотности тока с глубиной. Рассмотрим изменение плотности тока с глубиной в однородной среде вдоль вертикали, проходящей через центр питающего диполя (рис. 19.3, а). В точке М на глубине z плотность тока j_z равна геометрической сумме плотностей тока j_A и j_B от каждого из пи­тающих электродов. Из этого рисунка следует, что

(19.13)

Рис. 19.2. Схема различных дипольных установок

Рис. 19.3. Распределение плотности тока с глубиной:

а - векторы плотности тока j_A, j_B

б - зависимость относительной плотности тока от глубины

Поскольку

и ,

то подстановкой в формулу (19.13) найдем плотность тока на поверхности в точке О:

тогда относительная плотность тока

(19.14)

График относительной плотности тока от отношения глубины z к полудлине питающего диполя изображен на рис. 19.3, б. Он показывает, что при увеличении расстояния между питающими электродами относительная плотность тока возрастает.

Значит, увеличение расстояния между питающими электродами АВ дает возможность повысить глубину изучения разреза. На этом основаны методы электрических зондирований на постоянном токе.

Расчеты показывают, что до глубины протекает половина полного посылаемого тока, поэтому величина принимается за эффективную глубину проникновения постоянного электрического поля в среду. Однако эта оценка справедлива для нормального поля, т.е. поля в однородной проводящей среде. Примерно такое же распределение плотности тока будет в неоднородных средах со слабой дифференциацией удельного электрического сопротивления. При сильном контрасте удельных электрических сопротивлений слоев зависимости изменения относительной плотности тока с глубиной оказываются более сложными. В большинстве случаев глубина исследований находится в диапазоне 0,1-0,25AB.

Кажущееся электрическое сопротивление пород. Формула (19.11) позволяет определить сопротивление пород, если среда однородна. Однако в естественных условиях удельное электрическое сопротивление горных пород изменяется в широких пределах как в вертикальном, так и в горизонтальном направлениях. В случае неоднородных в электрическом отношении сред формула (19.11) не позволяет определить истинное удельное сопротивление пород, а дает некоторую расчетную величину, имеющую размерность удельного сопротивления, которая называется кажущимся сопротивлением пород:

(19.15)

Кажущееся сопротивление зависит от мощности и удельного электрического сопротивления отдельных слоев изучаемой части геологического разреза; оно определяется также размерами измерительной установки. Подробнее зависимость кажущегося сопротивления от характеристик геоэлектрического разреза и размеров измерительной установки рассмотрена в п. 19.2.2.