Часть 4 электроразведка

Электрическая разведка (электроразведка) включает значительно больше разнообразных методов, чем любая другая полевая геофизическая разведка. Это объясняется, с одной стороны, тем, что используемые в электроразведке поля могут быть постоянными или переменными во времени, а также могут возбуждаться как искусственными, так и естественными источниками. С другой стороны, с помощью электроразведки пытаются решать широкий спектр задач для различных глубин исследований, а сами горные породы имеют большой диапазон изменчивости их геоэлектрических свойств. Эти причины дают возможность разнообразить методы решения задач электроразведкой применительно к отдельным конкретным целям и объектам исследований.

Учитывая, что не все методы электроразведки могут быть применены при поисках и разведке нефтяных и газовых месторождений, здесь рассмотрим только те из них, которые широко используются для решения задач нефтегазовой геологии. В то же время необходимо иметь в виду, что еще большую роль электроразведка играет при поисках и разведке рудных месторождений, поскольку многие рудные объекты, являясь хорошими проводниками электрического тока, существенно влияют на характеристики наблюдаемых на поверхности Земли электромагнитных полей. Большое значение электроразведка имеет также при инженерно-геологических и гидрогеологических исследованиях: для изучения глубины залегания коренных пород под основание крупных инженерных сооружений и строений, выбора трасс тоннелей, трубопроводов, выявления и картирования водосодержащих пластов для бурения скважин на воду и др.

При поисках и разведке месторождений нефти и газа электроразведку используют главным образом для изучения структурных условий залегания интересующих слоев осадочных пород, с которыми связаны залежи нефти и газа (структурная электроразведка). В комплексе с другими полевыми геофизическими методами электроразведка находит применение для непосредственного выявления нефтегазовых залежей. Эта возможность ос­нована на том, что нефте- и газосодержащие породы обычно имеют значительно более высокое электрическое сопротивление по сравнению с водонасьпценными породами и обладают свойствами поляризуемости.

Глава 18 физические и геологические основы электроразведки

18.1. Основные представления об электромагнитном поле

В электроразведке используют как искусственные, так и естественные переменные и постоянные электромагнитные поля. Искусственное поле получают при пропускании постоянного и переменного электрического тока через заземленные питающие электроды (гальванический способ) или через электрический контур на поверхности земли в виде петли достаточных размеров (индукционный способ). Примером естественного переменного электромагнитного поля является магнитотеллурическое поле, наводимое в Земле процессами взаимодействия солнечного излучения с ее магнитосферой.

Компоненты электромагнитного поля. Распределение электромагнитного поля в среде подчинено законам электродинамики. Поле представляют в виде суммы двух изменяющихся во времени полей - электрического и магнитного, которые, взаимодействуя друг с другом, образуют единое электромагнитное поле. Взаимодействие электрического и магнитного полей обусловливает распространение в среде электромагнитных волн, характеристики которых (амплитуда, частота, скорость и т.п.) зависят от свойств среды (электрического сопротивления, диэлектрической и магнитной проницаемости).

Электромагнитное поле в вакууме представляют двумя векторными компонентами, зависящими от пространственных координат и времени: напряженностью электрического поля Е(х, у, z, t) и магнитной индукцией В(х, у, z, t), которые определяют силы, действующие со стороны поля на заряды q (заряд в единице объема) и плотности тока j (заряд, переносимый в единицу времени через единичную площадку, перпендикулярную движению зарядов). В реальной среде для описания поля кроме векторов Е и В вводят дополнительные векторные компоненты, зависящие от состояния и свойств среды - электрическую индукцию D(x, у, z, t) и напряженность магнитного поля Н (х, у, z, t):

(18.1)

где - диэлектрическая; - магнитная проницаемость среды.

Уравнения электромагнитного поля. Уравнения Максвелла позволяют определить компоненты электромагнитного поля (Е, В, D и Н) в любых точках пространства и моменты времени, если известны источники поля, плотность тока j и плотность заряда q как функции координат и времени. В дифференциальной форме уравнения Максвелла имеют вид:

(18.2)

(18.3)

(18.4)

(18.5)

где j - плотность полного тока, причем первая компонента j представляет движение зарядов в проводнике и обусловлена токами проводимости, а вторая компонента - токами смещения. Токи смещения не связаны с движением зарядов, а возникают только в результате изменения электрического поля во времени. В непроводящей среде (например, в вакууме) полный ток соответствует токам смещения, в проводящей среде магнитное поле возбуждается как токами проводимости (движением зарядов), так и токами смещения (скоростью изменения поля D). Именно токами смещения объясняется рас­пространение радиоволн в вакууме.

Физический смысл уравнений Максвелла состоит в следующем. Уравнение (18.2) показывает связь вихревого магнитного поля с токами проводимости и смещения. Уравнение (18.3) представляет закон электромагнитной индукции Фарадея, согласно которому ЭДС индукции, наводимая в замкнутом проводящем контуре, равна (с обратным знаком) скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Уравнение (18.4) отражает факт отсутствия в природе источников магнитного поля в виде магнитных зарядов, аналогичных электрическим зарядам - магнитное поле возбуждается только электрическими токами. Уравнение (18.5) показывает, что поле D определяется плотностью распределения зарядов q и представляет обобщение закона Кулона для взаимодействия неподвижных электрических зарядов, согласно которому электрическое поле Е, создаваемое точечным электрическим зарядом Q в однородной изотропной среде с диэлектрической проницаемо­стью е, пропорционально величине заряда Q и обратно пропорционально квадрату расстояния до заряда:

(18.6)

Уравнения Максвелла нельзя рассматривать без учета уравнений (18.1), связывающих между собой основные векторы электромагнитного поля, а также без уравнения

(18.7)

представляющего закон Ома в дифференциальной форме. Здесь - удельная электропроводность (величина обратная удельному сопротивлению ).

Граничные условия для векторов электромагнитного поля. На поверхностях раздела сред, которыми являются геологические границы, параметры , и могут скачкообразно изменяться, в этом случае согласно формулам (18.2)—(18.5) на границах будут изменяться и компоненты Е, D, В и Н электромагнитного поля. Для решения задачи распределения электромагнитного поля в неоднородных средах уравнения Максвелла дополняют граничными условиями. На поверхности раздела двух сред с постоянными параметрами (в верхней среде - , и , в нижней среде - , и ) граничные условия сводятся к следующему:

1. Для нормальных компонент поля

(18.8)

где - поверхностная плотность электрических зарядов на границе.

2. Для касательных компонент поля

(18.9)

где 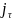- плотность поверхностного тока. При отсутствии в реальных средах идеальных проводников принимают, что .

С помощью условий (18.8), (18.9), а также формул (18.1) и (18.7) можно получить полный набор уравнений для нормальных и тангенциальных компонент векторов Е, В, D и Н.

Уравнения Максвелла для однородной среды и модели электромагнитного поля. Уравнения Максвелла (18.2)—(18.5) для однородной изотропной среды ( , и - постоянны) с учетом выражений (18.1) и (18.7) записываются в виде

(18.2)

(18.3)

(18.4)

(18.5)

Плотность свободных зарядов q в уравнении (18.13) равна нулю, так как в однородной среде они накапливаться не могут.

Из уравнений (18.10)—(18.13) путем некоторых преобразова­ний можно получить отдельные уравнения для электрического Е и магнитного H полей в виде волновых уравнений:

(18.14)

Этим уравнениям удовлетворяет так называемая волновая модель электромагнитного поля в непроводящей среде ( ), т.е. в изоляторе.

Квазистационарной модели электромагнитного поля соответствует медленно изменяющееся во времени поле, когда можно пренебречь вторыми производными по времени (или, что то же самое, токами смещения) и считать, что поле создается только токами проводимости:

(18.15)

Подобные уравнения называются уравнениями диффузии или теплопроводности. В нашем случае они описывают процесс распространения электромагнитных волн в проводящей среде

Стационарной модели электромагнитного поля соответствует независящее от времени поле, уравнениями которого являются

(18.16)

Все три упомянутые упрощенные модели электромагнитного поля используются в электроразведке. Однако в нефтегазовой электроразведке используют две модели - квазистационарную модель для медленно изменяющихся (низкочастотных) полей, когда токи смещения малы по сравнению с токами проводимости и поле не зависит от диэлектрической проницаемости среды (е принимается равной нулю), и стационарную модель, соответствующую постоянным токам и связанную только с проводимостью среды.

Глубина проникновения электромагнитного поля в геоэлектрические среды. Ограничимся представлением электро­магнитного поля в проводящей среде в виде распространяю­щейся в вертикальном направлении плоской гармонической волны:

(18.17)

После подстановки выражений (18.17) в уравнения (18.15) и сокращения на временной фактор получим уравнения диффузии в виде

(18.18)

где параметр

(18.19)

является соответствующим квазистационарному полю комплексным волновым числом, характеризующим среду при протекании в ней переменного тока. Поскольку , то

(18.20)

Приравняв действительную часть выражения (18.20) к из­вестной формуле волнового числа (см. П2.2), где λ- длина волны, получим

(18.21)

и, учитывая размерности ( , Т - период в с; [1/Ом м] и (Ом с)/м для вакуума), получим, что

(18.22)

и, соответственно, фазовая скорость электромагнитной волны

(18.23)

Решение уравнений (18.18), например, для электрической компоненты плоской гармонической волны может быть представлено как

где косинусоидальный член определяет волновой характер поля, а экспоненциальный - характеризует поглощение волны по мере ее распространения в положительном направлении оси z. Глубину проникновения поля h обычно оценивают толщиной слоя, в котором амплитуда волны уменьшается в е раз, т.е. . Согласно этой оценке величина h определяется мнимой частью волнового числа k (18.20), адекватной коэффициенту поглощения:

откуда с учетом (18.22) можно определить связь между глубиной проникновения поля h и периодом волны Т:

(18.24)

Из сказанного выше следуют основные выводы:

• глубина проникновения h электромагнитной волны тем больше, чем выше сопротивление горных пород. В изоляторе ( ) волна не затухает и распространяется на сколь угодно большую глубину. В хорошем проводнике( ) , что эквивалентно экранированию электромагнитного поля (например, радиоволн) металлическими проводниками. Явление затухания электромагнитных волн в проводнике называется скин-эффектом (по-английски skin - кожа), а величина h - толщиной скин-слоя;

• глубина проникновения h электромагнитной волны зависит от периода (частоты) волны - чем больше период (меньше частота), тем глубже проникает волна, и наоборот, она поглощается тем быстрее, чем короче ее период (больше частота);

• глубина проникновения постоянного тока ограничивается глубиной верхнего высокоомного слоя, т.е. слоя высокого сопротивления (для переменного тока такое ограничение отсутствует).