12.3. Редукции и аномалии силы тяжести

При вычислении аномалий силы тяжести, согласно формуле (12.18), необходимо сравнить наблюденные и нормальные значе­ния силы тяжести. Силу тяжести обычно измеряют на физиче­ской поверхности Земли, тогда как нормальные ее значения оп­ределены для поверхности сфероида, близкой к уровню моря. Возникающую проблему иллюстрирует рис. 12.2, где показан ле­жащий над уровнем моря слой с плотностью ст, верхняя граница которого определяется рельефом местности, а точка наблюдений на поверхности находится на высоте h относительно уровня мо­ря. Для вычисления аномалий силы тяжести необходимо, чтобы нормальное поле силы тяжести соответствовало уровню пункта наблюдений и условиям наблюдения. Поэтому в нормальные значения силы тяжести у вводится поправка или редукция за высоту точки наблюдения, снимающая эти расхождения и приводящая вычисленные нормальные значения к уровню пункта наблюдений, а из наблюденного значения поля g„ вычи­тают влияние масс, залегающих выше уровня моря. Задачу при­ведения к поверхности, называемую редуцированием силы тяже­сти, решают введением трех поправок: за высоту точки наблю­дения, за влияние масс промежуточного слоя и за рельеф мест­ности.

Поправка за высоту учитывает разницу значений нор­мального поля на уровне наблюдения и уровне моря. Притяже­ние масс, расположенных между физической поверхностью и уровнем моря, этой поправкой не учитывается. Поэтому поправ­ку за высоту называют также поправкой за «свободный воздух» или поправкой Фая. В грубом приближении, если форму Земли представить шаром, нормальное значение силы тяжести можно принять равным

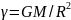, (12.22)

где М - масса Земли; R - средний радиус Земли.

Поправку за высоту определим как разность значений нор­мального поля на двух уровнях Земли с радиусами R и R+h:

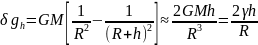(12.23)

При вычислении (12.23) учтено, что 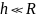. Подставив в выра­жение (12.23) численные значения входящих в него величин - значение силы тяжести и R - 6370 км, получим

(12.24)

где h - в м, - в мГал. Как следует из выражения (12.24), сила тяжести уменьшается примерно на 0,3 мГал на каждый метр вы­соты. Поправку за высоту вводят в значения со знаком минус при наблюдениях выше уровня моря и со знаком плюс при на­блюдениях ниже этого уровня.

Вводом поправки за притяжение промежуточного слоя учитывают влияние масс слоя, расположенного между указанной пунктиром вспомогательной поверхностью и уровнем моря и имеющего мощность, равную h (см. рис. 12.2). Этот плоскопараллельный слой принимается бесконечным и называется промежуточным слоем. Поправка за промежуточный слой вводится по формуле

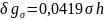(12.25)

где - средняя плотность пород промежуточного слоя. При пре­вышении высоты точки наблюдения над уровнем моря эту по­правку в наблюденные значения силы тяжести вводят со знаком минус. Если точка наблюдения находится ниже уровня моря, то знак поправки за промежуточный слой положительный.

Смысл поправки за рельеф состоит в том, чтобы скоррек­тировать наблюденные значения за влияние вызванных релье­фом масс, расположенных как выше, так и ниже верхней гори­зонтальной поверхности промежуточного слоя. Если около пунк­та наблюдений находится впадина рельефа, то учитывается не­достаток масс, если возвышенность - то избыток масс. При вводе поправки за промежуточный слой автоматически вычитается влияние отсутствующих во впадине масс, что приводит к умень­шению силы тяжести. При наличии возвышенности ее массы также уменьшают наблюденное значение силы тяжести, посколь­ку сила их притяжения направлена вверх. Поэтому поправку за рельеф вводят в всегда со знаком «плюс».

Поправки за рельеф представляются в виде суммы грави­тационных влияний кольцевых или прямоугольных зон, окру­жающих каждую из точек наблюдения. Для этого существуют специальные методики расчета поправок и соответствующее про­граммное обеспечение. Эти поправки должны определяться осо­бенно тщательно при измерениях на сильно пересеченной мест­ности.

Суммарная поправка за высоту, промежуточный слой и рель­еф называется поправкой Буге и при наблюдениях выше уровня моря она будет равна

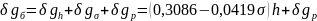(12.26)

Цель ввода поправки Буге - получить картину вариаций силы тяжести, зависящую только от горизонтальной неоднородности распределения плотностей горных пород, залегающих ниже по­верхности нормального сфероида. После введения этих поправок получают уточненное по сравнению с (12.18) выражение для аномального значения силы тяжести, получившее название ано­малии Буге.

(12.27)

Профили и карты аномалий силы тяжести в редукции Буге яв­ляются основным материалом для последующей интерпретации гравиразведочных данных.

Описанные выше поправки удовлетворяют большинству стан­дартных гравиметрических съемок, однако в особых случаях вы­сокоточных съемок и, наоборот, съемок регионального характера поправки требуют уточнения, а также требуется ввод дополни­тельных поправок.

В первом приближении считается, что гравитационное поле постоянно, однако реально оно меняется во времени. Медленные изменения связаны с плавными процессами внутри Земли, одна­ко существуют и более быстрые изменения, вызываемые притя­жением Луны и Солнца, а также собственными колебаниями Земли, вызываемыми землетрясениями. Силы притяжения Луны и Солнца создают упругие приливы в твердой оболочке Земли, амплитуды которых могут достигать до 70 см. Важно, что в от­личие от других причин эти приливы являются периодическими и их амплитуду можно оценить для любого заданного момента времени в любой точке. Поэтому при высокоточных гравиметри­ческих наблюдениях необходимо вводить поправки за притя­жение Луны и Солнца, поскольку они могут превышать точ­ность измерений.

Определяющую роль при вычислении аномалий Буге играет выбор плотности промежуточного слоя: если плотность принять слишком малой, то возможна прямая корреляционная зависи­мость значений аномалий от рельефа физической поверхности; если же плотность слоя завышена, то будет наблюдаться отрица­тельная корреляционная зависимость. При определении анома­лий силы тяжести берутся разные варианты плотности промежу­точного слоя: средняя плотность осадочного чехла 2,30 г/см³, средняя плотность земной коры 2,67 г/см³, а также истинная (реальная) плотность промежуточного слоя по результатам лабо­раторных измерений образцов горных пород.

Отсутствие корреляции аномалий Буге с высотами физиче­ской поверхности справедливо для небольших по размерам об­ластей. При рассмотрении больших по размерам областей земной поверхности оказывается, что между значениями аномалий Буге и высотами существует достаточно тесная связь, однако если по­правку за массы промежуточного слоя не учитывать, то такой связи не наблюдается. Следовательно, образующие земную кору массы в региональном плане не оказывают особого влияния на значения гравитационного поля, что можно объяснить только компенсацией масс: избытку масс над земной поверхностью (горным массивам) соответствует недостаток масс под ней и, на­оборот, недостатку масс на дневной поверхности соответствует избыток масс под поверхностью Земли. На явление компенсации масс указывает наличие значительных отрицательных аномалий Буге в горных областях и положительных - в областях с пони­женным рельефом. Это обстоятельство привело к возникновению теории изостазии. Под изостазией понимается равновесное со­стояние, в котором находятся литосфера и верхняя мантия. Со­гласно этой теории, на некоторой определенной глубине должна существовать поверхность равного давления со стороны вышеле­жащих масс - поверхность компенсации.

Литосфера имеет различные мощности и плотности, подчи­няющиеся определенным закономерностям. Одинаковые по пло­щади основания отдельных вертикальных блоков литосферы должны оказывать одинаковое давление на поверхность компен­сации. Существует три гипотезы изостатической компенсации - Пратта, Эри и Венинг-Мейнеса. Первые две гипотезы исходят из того, что земная кора состоит из отдельных свободно переме­щающихся относительно друг друга блоков.

По гипотезе Пратта литосфера состоит из отдельных блоков одинаковой массы, но различной плотности (рис. 12.3, а). Со­гласно закону Архимеда, блоки одинаковой массы погружаются в магму на одинаковую глубину. Давление на поверхность ком­пенсации S, расположенную на этой постоянной глубине Т от уровня моря, будет одинаковым по всей Земле. Тогда условие равновесия по Пратту можно записать следующим образом - для континентов: 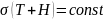; для океанов: 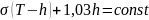. Здесь - плотность каждого из блоков; Н - высота над уровнем моря; h - глубина моря; 1,03 - плотность морской воды, г/см³.

По гипотезе Эри литосфера также состоит из отдельных бло­ков, но плотность их одинакова. Блоки плавают в более плотной, но вязкой астеносфере (см. рис. 12.3, б). Согласно закону Архи­меда, чем выше блок, тем глубже он погружается в астеносферу. Следовательно, мощность земной коры для горных областей должна быть больше (т.е. существуют корни гор), для океаниче­ских областей - меньше. 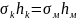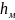Согласно этой гипотезе, , где и — плотность и мощность коры, и - плотность верх­ней мантии и глубина погружения коры в мантию. Поверхность одинакового давления в данном случае соответствует глубине погружения самого высокого блока. Из рис. 12.3, б видно, что нижняя граница земной коры является зеркальным отображени­ем физической поверхности Земли - чем выше дневная поверх­ность, тем глубже залегает нижняя граница земной коры и на­оборот.

Рис. 12.3. Схемы изостазии:

а - по Пратту; б - по Эри; в - по Венинг-Мейнесу

Гипотеза Венинг-Мейнеса учитывает силу сцепления между соседними блоками и представляет усовершенствованную гипоте­зу Эри, когда литосфера рассматривается в виде некоторой упру­гой плоской пластины, которая прогибается под действием масс, возвышающихся над уровнем моря (рис. 12.3, в). Особенности ги­потез Эри и Венинг-Мейнеса подтверждаются имеющимися сейсмическими данными о глубинном строении земной коры: мощ­ность земной коры под континентами находится в пределах от 30 до 70 км, в то время как мощность океанической коры изменяет­ся от 5 до 15 км. В складчатых областях континентов горы поднимаются над уровнем моря на 4...8 км, а земная кора под ними погружается в среднем на глубину 40...60 км; в платформенных областях континентов земная кора углубляется на 30...35 км.

Схема изостазии является основой для введения специаль­ной поправки при вычислении аномалий силы тяжести - изостатической поправки. Она состоит из двух частей: первая снимает влияние всех масс над уровнем моря - это топографи­ческая поправка (ее не следует путать с поправкой за окружающий рельеф), вторая добавляет влияние компенсирую­щих масс, поместив их внутрь Земли так, чтобы дополнить зем­ную кору до ее невозмущенного состояния (до постоянной плот­ности в гипотезе Пратта или до постоянной мощности в гипотезе Эри).

После введения этих двух поправок точка наблюдений ока­жется находящейся в воздухе над лишенной всех неровностей поверхностью Земли. Поэтому для приведения силы тяжести к уровню моря требуется введение поправки за высоту (свободный воздух), равной 0,3086h. Изостатическая аномалия силы тя­жести

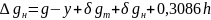(12.28)

Изостатическая поправка обычно уменьшает аномалии силы тяжести и приводит к их сглаживанию. В практике гравиразведки изостатические поправки вводятся только при работах регио­нального характера.